
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы первичной обработки выборки
Пусть интересующая нас случайная величина Х принимает в выборке значение х 1 п 1 раз, х 2 – п 2 раз, …, хк – пк раз, причем
Вариационный ряд, заданный в таком виде, называют дискретным Пример 2.1. На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие 60 значений: 3; 1; 3; 1; 4; ï 1; 2; 4; 0; 3; ï 0; 2; 2; 0; 1; ï1; 4; 3; 1; 1; 4; 2; 2; 1; 1; ï 2; 1; 0; 3; 4; ï 1; 3; 2; 7; 2; ï0; 0; 1; 3; 3;
1; 2; 1; 2; 0; ï 2; 3; 1; 2; 5; ï 1; 2; 4; 2; 0; ï 2; 3; 1; 2; 5. Выполним операции ранжирования (операция – ранжирование опытных данных, результатом которого являются значения, расположенные в порядке неубывания) и группировки. В результате были получены семь значений случайной величины (варианты): 0; 1; 2; 3; 4; 5; 7. При этом значение 0 в этой группе встречается 8 раз, значение 1 – 17 раз, значение 2 – 16 раз, значение 3 – 10 раз, значение 4 – 6 раз, значение 5 – 2 раза, значение 7 – 1 раз. Вычисленные значения частот и частностей приведены в табл. 2.1. Таблица 2.1
Таким образом, получен дискретный ряд:
где в скобках указаны соответствующие частоты. В отличие от исходных данных, этот ряд позволяет делать некоторые выводы о статистических закономерностях. Пример. При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Размах выборки равен 5. Статистический ряд для абсолютных и относительных частот имеет вид:
◄
Пример. Дана выборка, состоящая из чисел: 3.2, 4.1, 8.1, 8.1, 6.7, 4.4, 4.4, 3.2, 5.0, 6.7, 6.7, 7.5, 3.2, 4.4, 6.7, 6.7, 5.0, 5.0, 4.4, 8.1. Составить статистический ряд распределения абсолютных и относительных частот. Объем выборки п = 20. Перепишем варианты в порядке возрастания: 3.2, 3.2, 3.2, 4.4, 4.4, 4.4, 4.4, 4.4, 5.0, 5.0, 5.0, 6.7, 6.7, 6.7, 6.7, 6.7, 7.5, 8.1, 8.1, 8.1. Составлен так называемый вариационный ряд, который показывает, что выборка состоит из шести вариант. Составим статистический ряд:
(относительная частота Если число возможных значений дискретной случайной величины достаточно велико или наблюдаемая случайная величина является непрерывной, то строят интервальный вариационный ряд, под которым понимают упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частностями попаданий в каждый из них значений случайной величины. Как правило, частичные интервалы, на которые разбивается весь интервал варьирования, имеют одинаковую длину и представимы в виде
где Длину
где
После нахождения частных интервалов определяется, сколько значений случайной величины попало в каждый конкретный интервал. Для определенности считают левый конец интервала закрытым, а правый – открытым. В интервал включают значения, большие или равные нижней границе и меньшие верхней границы. ¨ Пример 2.3. При изменении диаметра валика после шлифовки была получена следующая выборка (объемом
Необходимо построить интервальный вариационный ряд, состоящий из семи интервалов.
Решение. Так как наибольшая варианта равна 23.8, а наименьшая 10.1, то вся выборка попадает в интервал (10,24). Мы расширили интервал (10.1,23.8) для удобства вычислений. Длина каждого частичного интервала равна
а соответствующий интервальный вариационный ряд представлен в табл. 2.2. Таблица 2.2
От интервального ряда можно перейти к дискретному статистическому ряду, взяв на каждом интервале (хi, xi+1) за отдельное значение хi* величину
являющуюся серединой этого интервала. Приемы обработки выборок 1. Ранжирование – упорядочение элементов выборки в порядке возрастания. Одинаковые значения повторно включаются в ранжированный ряд. 2. Чтобы избежать дальнейших громоздких действий с выборкой, строится группированный статистический ряд: – определяется диапазон выборки [ x min, x max]; – находится шаг разбиения
– вычисляются границы интервалов (с точностью не менее трех знаков после запятой): z 0= x min, z 1 = z 0 + h, z 2 = z 1 + h, z 3 = z 2+ h; z 4 = z 3 + h, z 5 = z 4 + h; и т.д. – находятся значения середин интервалов
– вычисляются частоты попадания значений в интервалы: n 1, n 2, n 3, n 4, n 5…, при этом должна выполняться контрольная сумма: – находятся относительные частоты попадания значений в интервалы: w 1 = n 1 /n, w 2 = n 2 /n, w 3 = n 3 /n, w 4 = n 4 /n, w 5 = n 5 /n, и т.д. Здесь контролируется выполнение суммы: – вычисляются высоты ступеней гистограммы
В результате получаем таблицу группированного статистического ряда:
Группированный статистический ряд, включая в себя строки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.187.103 (0.025 с.) |
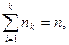 где п – объем выборки. Тогда наблюдаемые значения случайной величины х 1, х 2,…, хк называют вариантами, а п 1, п 2,…, пк – частотами. Отношение частоты данного варианта к общей сумме частот называется частностью (или относительной частотой) и обозначается
где п – объем выборки. Тогда наблюдаемые значения случайной величины х 1, х 2,…, хк называют вариантами, а п 1, п 2,…, пк – частотами. Отношение частоты данного варианта к общей сумме частот называется частностью (или относительной частотой) и обозначается  ,
,  , т.е.
, т.е.  или
или 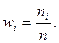 Разность между максимальным и минимальным элементами выборки называется размахом выборки. Последовательность вариант, записанных в порядке возрастания, называют вариационным ряд ом, а перечень вариант и соответствующих им частот или относительных частот – статистическим рядом:
Разность между максимальным и минимальным элементами выборки называется размахом выборки. Последовательность вариант, записанных в порядке возрастания, называют вариационным ряд ом, а перечень вариант и соответствующих им частот или относительных частот – статистическим рядом:


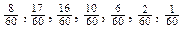
 ,
, ). ◄
). ◄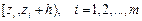 ,
,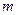 - число интервалов. Количество интервалов рассчитывают по эмпирической формуле Старджеса:
- число интервалов. Количество интервалов рассчитывают по эмпирической формуле Старджеса:  , где n – объем выборки
, где n – объем выборки следует выбирать так, чтобы построенный ряд не был громоздким, но в то же время позволял выявлять характерные изменения случайной величины. Для вычисления
следует выбирать так, чтобы построенный ряд не был громоздким, но в то же время позволял выявлять характерные изменения случайной величины. Для вычисления  ,
, – наибольшее и наименьшее значения случайной величины. Если окажется, что
– наибольшее и наименьшее значения случайной величины. Если окажется, что  .
.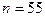 ):
): . Получаем следующие семь интервалов:
. Получаем следующие семь интервалов:



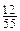

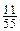


 , i = 1,..., 5,:
, i = 1,..., 5,: ,
,  ,
,  ,
,  ,
,  и т.д.
и т.д. .
.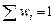 .
. :
:  ,
,  ,
, 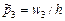 ,
, ,
,  ит.д. Проверка:
ит.д. Проверка:  .
.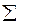

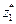









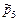
 и wi, является аналогом закона распределения дискретной модели исследуемой нами генеральной совокупности.
и wi, является аналогом закона распределения дискретной модели исследуемой нами генеральной совокупности.


