
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки параметров
Распределения Пусть требуется изучить количественный признак генеральной совокупности. Располагая лишь выборочными значениями признака, можно оценить, а не определить точно значения параметров закона или числовых характеристик признака; эти оценки будут случайными и меняться от выборки к выборке. Поэтому важно не только знать оценки неизвестных величин, полученные на основе выборочных данных, но и понимать меры их надежности. Цель любого оценивания – получить как можно более точное значение неизвестной характеристики признака генеральной совокупности по данным выборочного наблюдения. Статистической оценкой неизвестной величины (неизвестного параметра теоретического закона распределения или неизвестной числовой характеристики признака генеральной совокупности) называют функцию от наблюдаемых значений признака как независимых случайных величин. Точечной называют статистическую оценку, которая характеризуется одним числом. Интервальной называют оценку, которая задаётся двумя числами – концами интервала, покрывающего неизвестную величину, внутри которого может находиться оцениваемый параметр генеральной совокупности. Генеральная совокупность характеризуется двумя сторонами: 1) видом распределения (например, равномерное, нормальное, Пуассоновское и т.д.); 2) параметрами распределения (например, математическое ожидание, среднее квадратическое отклонение и т.п.). В связи с этим существует два класса оценок: оценки вида распределения и оценки параметров распределения. К статистической оценке предъявляется ряд естественных требований (несмещённость, состоятельность, эффективность), которые обеспечивают в некотором смысле её «доброкачественность». Определения несмещённой, состоятельной, эффективной оценок смотри в п.3.
1. Точечные оценки параметров распределения. Несмещённой и состоятельной оценкой генеральной средней (математического ожидания признака Х генеральной совокупности) является выборочная средняя 1. Выборочным средним называется среднее арифметическое значений случайной величины, принимаемых в выборке:
где xi – варианты, ni - частоты. Замечание. Выборочное среднее служит для оценки математического ожидания исследуемой случайной величины.
Выборочной дисперсией называется
Выборочным средним квадратическим отклонением –
Так же справедлива следующая формула для вычисления выборочной дисперсии:
Исправленная выборочная дисперсия
Исправленное выборочное среднее квадратическое отклонение -
Пример. Найдем числовые характеристики выборки, заданной статистическим рядом
■▬▬▬►
2. Другими характеристиками вариационного ряда являются: - мода М0 – варианта, имеющая наибольшую частоту (в предыдущем примере М0 = 5). - медиана т е - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно (n = 2 k + 1), то me = xk+ 1, а при четном n = 2 k Оценки начальных и центральных моментов (так называемые эмпирические моменты) определяются аналогично соответствующим теоретическим моментам: - начальным эмпирическим моментом порядка k называется
В частности, - центральным эмпирическим моментом порядка k называется
В частности, ◄▬▬▬■ Для непрерывного распределения применяются те же формулы, но за значения 3. Получив статистические оценки параметров распределения (выборочное среднее, выборочную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближением соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться. Пусть Θ* - статистическая оценка неизвестного параметра Θ теоретического распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема п и вычислим для каждой из них оценку параметра Θ:
Статистическая оценка Θ* называется несмещенно й, если ее математичес-кое ожидание равно оцениваемому параметруΘ при любом объеме выборки: М (Θ*) = Θ. Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру. Однако несмещенность не является достаточным условием хорошего приближения к истинному значению оцениваемого параметра. Если при этом возможные значения Θ* могут значительно отклоняться от среднего значения, то есть дисперсия Θ* велика, то значение, найденное по данным одной выборки, может значительно отличаться от оцениваемого параметра. Следовательно, требуется наложить ограничения на дисперсию. Статистическая оценка называется эффективной, если она при заданном объеме выборки п имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется еще и требование состоятельности. Состоятельной называется статистическая оценка, которая при п →∞ стремится по вероятности к оцениваемому параметру (если эта оценка несмещенная, то она будет состоятельной, если при п →∞ ее дисперсия стремится к 0). Заданная таким образом оценка математического ожидания является несмещенной, то есть математическое ожидание выборочного среднего равно оцениваемому параметру (математическому ожиданию исследуемой случайной величины). Выборочная дисперсия, напротив, смещенная оценка генеральной дисперсии, и
Соответственно число Пример. Найти выборочное среднее, исправленную выборочную дисперсию и исправленное среднее выборочное отклонение для выборок, заданных в примерах 1 и 2. 1)
2) В выборке из примера 2 будем считать вариантами середины частичных интервалов, то есть определим точечные оценки для выборки
Тогда
Пример. При изучении производительности труда Х на одного работника было обследовано 10 предприятий и получены следующие значения (тыс. руб.): 4,2; 4,8; 4,7; 5,0; 4,9; 4,3; 3,9; 4,1; 4,3; 4,8. Определить выборочную среднюю, выборочную дисперсию, исправленное среднее квадратическое отклонение. По данной выборке объёма n=10 составим статистический ряд:
По формуле (1) найдется выборочная средняя:
По формуле (2) найдем выборочную дисперсию. Для этого вычислим
Тогда DB=20,382–20,25=0,132. Согласно (4а) S≈0,383. Смысл полученных результатов заключается в следующем. Средняя производительность труда на одного работника для изученных предприятий составила
Пример. Из генеральной совокупности извлечена выборка. -0,269 -0,786 0,585 -1,107 1,574 0,341 -1,309 -0,165 -0,483 0,525 1,620 0,206 0,346 -0,973 -0,363 0,660 1,084 0,903 1,387 1,261 0,786 1,107 0,341 0,525 1) Определить: выборочное среднее, выборочную и исправленную дисперсии, выборочное и исправленное среднее квадратичное отклонение. 2) Построить сгруппированный статистический ряд, гистограмму и эмпирическую функцию распределения. На основе анализа гистограммы и эмпирической функции распределения сделать предположение о виде распределения исследуемого признака. Занесем данные в таблицу и выстроим их по возрастанию (для построения группировки). Найдем сумму выборочных данных и выборочное среднее. Найдем выборочную
Таблица 3.
Исправленная выборочная дисперсия Количество интервалов рассчитаем по формуле Старджеса: Наименьшее значение равно –1,309, наибольшее значение равно 1,620. длина интервала находится по формуле Таблица 4.
Эмпирическая функция распределения – это графическое изображение относительных накопленных частот в виде ступенчатой линии.
Накопленная частота – это число вариант, меньших правой границы интервала. Относительная накопленная частота – это отношение накопленной частоты к объему выборки.
Рис. 4 По виду гистограммы можно сделать вывод, что данное распределение не является нормальным.
Рис. 5
2. Интервальные оценки параметров распределения. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальными оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки(предельность ошибки) (чем меньше δ, тем точнее оценка). Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью. Надежностью (доверительной вероятностью) оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ. Если заменить это неравенство двойным неравенством – δ < Θ* - Θ < δ, то получим: p (Θ* - δ < Θ < Θ* + δ) = γ. Таким образом, γ есть вероятность того, что Θ попадает в интервал (Θ*- δ, Θ*+ δ). Доверительным называется интервал, в который попадает неизвестный параметр с заданной надежностью γ; он является симметричной интервальной оценкой неизвестной величины Q.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.201.71 (0.032 с.) |
 .
.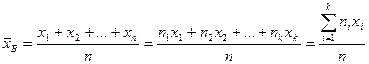 , (1)
, (1)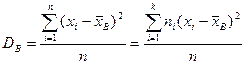 . (2)
. (2)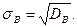 (3)
(3) . (4)
. (4)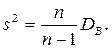 (4а)
(4а) .
.
 . В частности, в предыдущем примере
. В частности, в предыдущем примере 
 . (5)
. (5) , то есть начальный эмпирический момент первого порядка равен выборочному среднему.
, то есть начальный эмпирический момент первого порядка равен выборочному среднему. . (6)
. (6) , то есть центральный эмпирический момент второго порядка равен выборочной дисперсии.
, то есть центральный эмпирический момент второго порядка равен выборочной дисперсии. в этих формулах берутся, как правило середины вариант-интервалов. Таким образом, интервальный вариационный ряд заменяется дискретным рядом.
в этих формулах берутся, как правило середины вариант-интервалов. Таким образом, интервальный вариационный ряд заменяется дискретным рядом. Тогда оценку Θ* можно рассматривать как случайную величину, принимающую возможные значения
Тогда оценку Θ* можно рассматривать как случайную величину, принимающую возможные значения  Поэтому и вводится несмещенная оценка генеральной дисперсии – исправленная выборочная дисперсия
Поэтому и вводится несмещенная оценка генеральной дисперсии – исправленная выборочная дисперсия

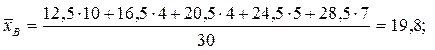
 ◄
◄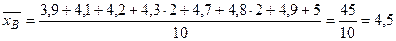 (тыс. руб.).
(тыс. руб.).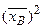 и
и  по формуле (4):
по формуле (4):
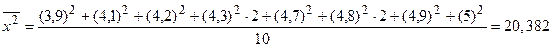
 =4,5 тыс. руб. Исправленное среднее квадратическое отклонение S описывает абсолютный разброс значений показателя Х и в данном случае составляет S=0,383 тыс. руб.◄
=4,5 тыс. руб. Исправленное среднее квадратическое отклонение S описывает абсолютный разброс значений показателя Х и в данном случае составляет S=0,383 тыс. руб.◄ и исправленную
и исправленную  дисперсии.
дисперсии. 0,736,
0,736,  0,858
0,858

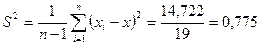 , исправленное среднеквадратическое отклонение
, исправленное среднеквадратическое отклонение 
 . Получим
. Получим  , округляем в большую сторону, k = 6.
, округляем в большую сторону, k = 6.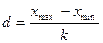 . «Упакуем» выборку в интервале [-1,311; 1,623], который разобьем на 6 частей длиной
. «Упакуем» выборку в интервале [-1,311; 1,623], который разобьем на 6 частей длиной  . Подсчитаем частоту
. Подсчитаем частоту  для каждого интервала и получим сгруппированный статистический ряд. Гистограмма – это фигура, составленная из прямоугольников, основаниями которых служат интервалы группировки. Высота hj j – того прямоугольника определяется по формуле
для каждого интервала и получим сгруппированный статистический ряд. Гистограмма – это фигура, составленная из прямоугольников, основаниями которых служат интервалы группировки. Высота hj j – того прямоугольника определяется по формуле 





