
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ранжировка и оценка в баллах
Под ранжировкой обычно понимают упорядочениезаданной совокупности объектов по степени проявления у них оцениваемого показателя качества, например, важности, модности, целесообразности, масштабности и др. В результате ранжировки каждому из оцениваемых объектов присваивается ранг – число, отражающее относительную степень предпочтительности данного объекта по сравнению с другими объектами из данной совокупности (в данном пункте изложение в значительной мере ведется в соответствии с работой [109]). Полученную в результате экспертизы ранжировку n объектов можно представить в виде последовательности n чисел:
(U1, U2,…, U n- 1, Un), (19)
где U i – ранг i –го объекта (i = 1,…, n). Если результаты экспертизы определяют на данном множестве объектов отношение строгого порядка (т.е. если с точки зрения эксперта все объекты четко различаются между собой по уровню качества), то ранг U i можно определить как натуральное число, на единицу большее, чем число объектов, имеющих более высокий уровень качества, чем i –й объект. Таким образом, наилучший из объектов получит ранг, равный 1, а наихудший – ранг, равный n. Пример 2.1. Пусть ранжировка пяти объектов { О 1, О 2, О 3, О 4, О 5} имеет следующий вид: (2, 5, 1, 3, 4) (20)
который является частным случаем (19). Таким образом, наилучшим был признан объект № 3 (его ранг U3 = 1), следующим по своему уровню качества данного признака признан объект № 1 (U1 = 2), а объект № 2 признан наихудшим среди данных пяти объектов (U2 = 5). Ранжировка (20) представляет собой тот факт, что на данном множестве определено отношение строгого порядка
О 3
(знак Заметим, что независимо от результатов ранжирования сумма Su всех рангов в (19) всегда будет равна сумме первых n чисел натурального ряда
Su = U 1 + U2 +…+ Un = 1 + 2 +…+ (n -1) + n =
поскольку при условии задания строгого порядка на множестве объектов любая их ранжировка (19) представляет собой перестановку первых n натуральных чисел. Если же некоторые из объектов по своему уровню качества оказались неразличимыми, то это означает, что на их множестве задается отношение квазипорядка. В этом случае принято говорить, что в ранжировке присутствуют связные ранги. Вполне логично потребовать, чтобы и в этом случае для рангов выполнялось условие, аналогичное условию (22), а именно
U 1 + U2 +…+ Un =
Чтобы выполнялось условие (23), объектам, качество которых в итоге экспертизы признано одинаковым, приписываются равные ранги по следующему правилу: общее значение ранга этих объектов полагается равным среднему арифметическому рангов, которые им «достались бы» при условии, что экспертиза смогла бы установить строгий порядок для всех оцениваемых объектов.
Для примера: пусть среди n объектов имеется n 1 объектов, имеющих наивысший уровень качества, n 2 объектов, чей уровень качества занимает второе место, и т. д., наконец, nk объектов, имеющих k -й (самый низкий из представленных в данной совокупности объектов) уровень качества. Тогда ранг каждого из ni объектов, относящихся к i -му уровню качества (i = 1,…, k), будет равен
т.е. среднему арифметическому рангов объектов, относящихся к данному уровню. Последнее выражение легко преобразовать к виду
n 1 + n 2 +… + ni -1 + Таким образом, все объекты имеющие вначале одинаковый ранг U i (поскольку по мнению экспертов имеют одинаковое качество), получат в соответствии с введенным правилом и (25) новые ранги. Пример. Пусть результаты оценивания качества пяти объектов имеют следующий вид[110]:
т. е. объекты О 1 и О 3 имеют одинаковое и притом наивысшее качество, а качество объектов О 2 и О 5 – одинаковое, но самое низкое. Тогда в соответствии с (25) объектам будут приписаны следующие ранги:
(1.5; 4.5; 1.5; 3; 4.5).
Поясним, как это получено. В данном примере выделено k =3 различных уровня качества, причем n 1 = 2, n 2 = 1, n 3 = 2. Таким образом, в частности, ранг объекта О 2 , относящегося к категории i = 3, будет согласно (25) равен
U2 = 2+1+ (2+1)/2 = 4.5.
Для ручного преобразования возможна и следующая схема приписывания рангов в случае наличия одинаковых оценок. 1. Выписать все оценки согласно полученным рангам (одинаковые оценки выписываются в произвольном порядке). 2. Определить номера места каждого объекта в данном упорядоченном ряду. Для данного примера это будет выглядеть так
3. Для тех групп объектов, у которых оценки оказались равными, найти среднее арифметическое их мест. В примере таких групп две. Первая группа - объекты О 1 и О 3 . Их среднее арифметическое - (1+2)/2=1.5. Вторая группа – объекты О 2 и О 5 . Их средне арифметическое – (4+5)/2=4.5. 4. Приписать ранги с учетом произведенных расчетов. Теперь остается приписать новые ранги каждому объектов. В данном случае имеем
Примечание. Требование (23) постоянства суммы рангов и вытекающее из него выражение (25) введены исключительно для удобства последующей обработки результатов ранжировки. От эксперта, очевидно, не следует ожидать результата в виде рангов, которые будут удовлетворять (25). Более естественным для него представить результаты оценки качества в виде, аналогичном (26) или в каком-либо ином, из которого далее путем подсчета можно получить ранги, удовлетворяющие (25), однако, это уже является задачей лица, обрабатывающего результаты экспертизы, а не самого эксперта. Отметим существенное различие между двумя постановками задачи, которая может быть предложена эксперту: 1) ранжировать данную совокупность объектов, 2) отнести каждый из объектов к одной из заранее определенных градаций, обозначающих ту или иную степень проявления данного качества. И в первом и во втором случаях на множестве объектов будет определено одно и то же отношение (квазипорядка или, если все объекты различны по своему уровню качества, строгого порядка). Однако в первом случае ординальная шкала (данные рассуждения относятся и к номинальной шкале), по которой производится оценивание, заранее не определена: она формируется самим экспертом в процессе оценивания, так что новая градация возникает всякий раз, когда эксперт обнаруживает объект, имеющий уровень качества, отличный от уровня рассмотренных ранее объектов. Во втором случае шкала, которой должен пользоваться эксперт, известна заранее, до проведения оценки качества данной совокупности объектов. Пример. Для иллюстрации рассмотрим в качестве продолжения предыдущего примера возможный вариант результатов оценивания двумя экспертами совокупности из 5 объектов: { О 1, О 2, О 3, О 4, О 5} по шкале, имеющей 5 возможных градаций рассматриваемого показателя качества. Результаты оценивания качества пяти объектов представлены в таблице 1.
Табл.1.
Из этой таблицы видно, что второй эксперт оценивает все объекты более «строго», чем первый. Кроме того, по мнению второго эксперта, объект О 4 ближе по своему уровню качества к объектам О 1 и О 3, чем к объектам О 2 и О 5. В то же время, если рассмотреть полученные от двух данных экспертов ранжировки, то они, как нетрудно заметить, будут одинаковы и обе совпадают с (26). Таким образом, если бы экспертам было предложено ранжировать всего лишь данную совокупность объектов, то каждый из них представил бы свои результаты оценивания в виде ранжировки (26), из которой следовало бы, что оба эксперта способны выделить всего три возможные градации проявления данного показателя качества.
Бальная оценка. Задача упорядочениязаданной совокупности объектов по степени проявления у них оцениваемого показателя качества может решаться путем приписывания каждому из ни соответствующего балла. Балл – определяемое экспертным путем числовое значение, указывающее на степень проявления оцениваемой характеристики, для которого: · заданы максимально и минимально возможные значения; · определены общие критерии (правила), по которым количество начисляемых баллов может увеличиваться или уменьшаться; · задан минимально допустимый «шаг» изменения баллов – своего рода «цена деления» балльной шкалы[111]. Оценка качества объекта, выраженная в баллах, не зависит от качества других объектов в данной совокупности. Эта оценка содержит больше информации, чем ранжировка объектов, или оценка в заданной заранее шкале порядка (разумеется, если число ее градаций меньше, чем максимально возможное значение числа баллов). Так, например, пусть уровень качества оценивается в 20-балльной шкале и пусть вновь, как и в предыдущем примере, двое экспертов произвели оценивание пяти объектов. Пусть результаты оценивания имеют вид, представленный в таблице 2. В некоторых задачах на основе полученного объектом числа баллов ему должна быть выставлена оценка в ординальной шкале, имеющей заранее фиксированное число градаций. При этом должно быть указано соответствие между диапазонами значений баллов и пунктами данной ординальной шкалы. Именно таким образом осуществляется перевод из 100-балльной шкалы в шкалу оценок в британской системе высшего образования (см. табл. 3). Табл.2. Пример результатов оценивания пяти объектов по 20-балльной шкале
Табл.3. Шкалы оценок и баллов, применяемые в британской системе высшего образования
Вернемся к данным примера, описанным в табл. 1 и табл.2. Пусть указанное выше соответствие между градациями и диапазонами баллов имеет вид, представленный в таблице 4.
Табл.4. Соответствие между ординальной шкалой и 20-балльной шкалой
Применив установленное в табл.4 соответствие к результатам оценивания из табл.2, мы получим результаты оценивания двух объектов, в точности совпадающие с приведенными в табл.1. При этом можно заметить, что данные табл.2 содержат в себе больше сведений, позволяющих сравнивать уровень качества данных объектов, чем данные из табл.2. Так, в частности, по мнению второго эксперта, объект О 3 имеет более высокий балл, чем объект О 1 , хотя оба эти объекта получают одинаковую оценку s 2 («выше среднего») в заданной порядковой шкале. Кроме того, с помощью оценок в баллах можно заметить, что объект О 4 оценен первым экспертом выше, чем вторым экспертом (на один балл), тогда как из оценок этого объекта в порядковой шкале это не усматривается. Наконец, если на основе данных табл.2 построить ранжировки данных пяти объектов, то для первого эксперта ранжировка имеет вид (26) и содержит связные ранги, тогда как для второго эксперта она выглядит как (21) и задает отношение строгого порядка. Оценки в баллах - более информативный вид данных о сравнительном уровне качества данной совокупности объектов, чем оценки, представленные в ординальной шкале, имеющей наперед заданное число градаций. Разумеется, это справедливо, если максимально возможный балл, получаемый объектом, существенно больше, чем число градаций указанной ординальной шкалы, то есть если каждой градации отвечает целый диапазон баллов, как, например, в таблице 4. В свою очередь оценки в ординальной шкале, имеющей достаточно большое число градаций, являются более информативными, чем результаты ранжировки (как видно, например, из сравнения (26) и данных таблицы 1). Заметим попутно, что всякая ранжировка, очевидно, порождает определенную ординальную шкалу (шкалу строгого порядка), имеющую столько градаций, сколько различимых уровней качества было выявлено в результате ранжирования. Пунктами такой шкалы могут служить принимаемые за эталоны уровни качества объектов, представляющих различные ранги. Так, например, ранжировка (26) определяет шкалу, имеющую 3 различных градации, в качестве пунктов которой можно взять уровни качества объектов, например, О1 , О4 и О2. Говоря о сравнении оценок в баллах и в рангах, также следует отметить, что оценки в баллах менее «устойчивы» в том смысле, что они более подвержены влиянию субъективных факторов. Оценивающее лицо, являясь экспертом в данной предметной области, как правило, имеет определенные основания, чтобы считать, что объект Оi имеет более высокий уровень качества, чем объект О. Эти основания могут быть объяснены, и результат Оi
Наряду с отношением порядка для оценок в баллах определены и другие бинарные отношения. Так, можно говорить о том, что оценка объекта Оi на столько-то баллов выше, чем оценка объекта Оj. Казалось бы, это означает, что показатель качества, оцениваемый в баллах, можно рассматривать как измеряемый в интервальной шкале. Однако такой вывод можно сделать лишь в случае, если имеется вполне строгое правило, согласно которому возрастание уровня качества должно приводить к увеличению оценки на 1 балл. На практике это, как правило, далеко не так: даже в случае оценок в фигурном катании, где существуют достаточно четкие критерии оценивания, вряд ли можно утверждать, что различие между качеством выступлений, оцененных баллами 4.8 и 4.9 такое же, как между качеством выступлений, оцененных баллами 5.9 и 6.0. Поэтому более правильным представляется рассматривать оценки качества, выраженные в баллах, как оценки в ординальной шкале, число возможных градаций которой во многом зависит от самого оценивающего субъекта, точнее, от его способности различать степени проявления оцениваемого качества у наблюдаемых объектов. Вместе с тем, внешняя «похожесть» шкалы баллов на шкалу интервалов служит своего рода оправданием широкого использования такого показателя, как средний балл, который имеет смысл для шкалы интервалов, но не является осмысленным для шкалы порядка. В связи с последним замечанием возникает вопрос о том, существует ли адекватный осмысленный аналог понятию «среднее значение» применительно к данным, представленным в нечисловой форме. В самом деле, в ряде случаев мы располагаем оценками в баллах или по заранее заданной порядковой или номинальной шкале, и при этом задача состоит в сравнении среднего уровня показателя качества у двух совокупностей объектов (или у одной совокупности, но по различным показателям, как в случае сравнения успеваемости группы студентов по двум различным дисциплинам).
Для переменных, измеряемых по номинальной шкале, традиционное понятие «среднее значение» нуждается в корректировке. В противном случае неясно, что следует понимать под средним значением, например, таких показателей, как «цвет автомобиля, предпочитаемого данной категорий населения» или «отрасль экономики, в которой занято большинство населения данного региона». Поэтому при использовании номинальной шкалы «среднее» целесообразнее интерпретировать как наиболее часто встречаемое в данной совокупности объектов. В силу этих соображений естественным показателем, характеризующим среднее для показателей, измеряемых в номинальной шкале, служит мода.Напомним, что модой случайной переменной называется такое ее значение mod (X), при котором достигается максимум ее плотности распределения: max f(x) = f(mod (X) ), если речь идет о непрерывной переменной, или максимум по всем возможным значениям xi вероятности того, что X примет значение xi, если переменная X - дискретна:
max {P(X = xi)}= P(X = mod (X) ).
Большинство встречаемых в теории вероятностей распределений являются унимодальными, то есть имеют единственную моду. Однако на практике истинное распределение часто бывает неизвестно, оценка плотности f(x) или вероятностей {P(X = xi)} производится с помощью выборки наблюдений, при этом максимум зачастую может оказаться не единственным. Применение моды в качестве оценки показателя средней тенденции имеет ряд недостатков, в частности, если мода не единственна, т.е. если максимум (локальный) достигается при нескольких различных категориях, то не единственной будет и искомая оценка. Если показатель качества измеряется в порядковой шкале, то в качестве характеристики среднего значения обычно используется медиана, обозначаемая, например, как med (X). Пусть носителем шкалы служит строго упорядоченное множество градаций S = { s 1
P(s 1) + …+ P(s M- 1) < 0.5, P(s 1) + …+ P(s M- 1) + P(s M) ³ 0.5 (27)
Иначе говоря, условие
med (X) = s M следует понимать таким образом, что не менее 50 % объектов в данной совокупности имеют уровень качества не ниже, чем s M, и не менее 50 % объектов – имеют этот уровень не выше, чем s M. В тех редких случаях, когда сумма вероятностей, соответствующих первым i градациям, в точности равняется 0.5, обе градации s i и s i+ 1 могут в равной мере служить в качестве медианы. На практике вероятности P(s i) чаще всего неизвестны и в качестве их оценок используются соответствующие относительные частоты ni / n, полученные с помощью выборки наблюдений. На основе этих оценок из условий (27) находят значение показателя (категорию), называемую выборочной медианой. Пример. Для данных 25 наблюдений, представленных в следующей таблице
и понимаемых как результаты измерений в порядковой шкале с возможными градациями{ s 1, s 2,…, s 6 }, выборочной медианой будет служить градация s 3 , поскольку
n 1 / n + n 2 / n = 3/25+ 9/25 = 0.48 < 0.5; n 1 / n + n 2 / n + n 3 / n = 3/25+ 9/25 + 6/25 = 0.72 > 0.5.
В целях подготовки обоснования решения по выбору одной из альтернатив после проведения ранжирования и бальной оценки нескольких альтернатив целесообразно введение соответствующих числовых оценок. При этом могут использоваться самые различные методы, описание которых широко опубликовано (см, например, [112]). Здесь мы приведем лишь два метода: метод парных сравнений и метод последовательного сравнения. Практические примеры применения этих конкретных методов хорошо изложены в работе [113]. Метод парных сравнений. Эксперту предлагается рассмотреть все пары из заданных · если альтернатива · если эксперты среди двух альтернатив не могут выбрать более предпочтительной, т.е. · если альтернатива Очевидно, что полученные оценки можно записать в виде квадратной матрицы Рассмотрим следующий условный пример. По результатам работы фирмы решается вопрос о распределении полученной прибыли. Рассматриваются альтернативы: 1. выдать премию сотрудникам; 2. дать дополнительный оплачиваемый отпуск; 3. вложить полученные средства в ценные бумаги; 4. вложить средства в развитие фирмы. Пусть результаты работы эксперта зафиксированы в виде следующей матрицы
Суммы элементов строк соответственно равны: 6, 2, 3, 5. Следовательно, по результатам данной экспертизы приоритетной можно признать альтернативу Метод последовательного сравнения (иногда его называют методом Черчмена-Акоффа). Пусть в результате экспертизы эксперты установили некоторые оценки (числовые или бальные). В этом случае возможны ситуации, когда их оценки будут взаимно противоречивы. Для снятия этих противоречий и может применяться метод последовательного сравнения. Основные предположения, на которых основан метод, состоят в следующем [114]: • каждой альтернативе аi ( • если альтернатива ai предпочтительнее альтернативы аj, то φ(аi)>φ(аj),если же альтернативы ai и аj равноценны, то φ(аi)=φ(аj); • если φ(аi) и φ(аj)оценки альтернатив ai и аj то φ(аi)+φ(аj) соответствует совместному осуществлению альтернатив ai и аj. Последнее предположение об аддитивности оценок альтернатив является из этих трех наиболее сильным и занимает центральное место в методе последовательного сравнения. Пусть альтернативы а 1, а2,..., aN ранжированы по предпочтительности. Для удобства изложения предположим, что наиболее предпочтительна альтернатива а 1, за ней следует а 2 и т.д. Далее эксперт указывает предварительные численные оценки φ(аi) для каждой из альтернатив (удобно оценку 1 предписывать наиболее предпочтительной альтернативе, тогда остальные оценки располагаются между 0 и 1 в соответствии с их предпочтительностью). Вначале эксперт рассматривает альтернативу a 1и сравнивает ее с суммой альтернатив а2,...,aN. Он должен высказать свое мнение относительно вопроса: альтернатива a 1 предпочтительнее суммы всех остальных или нет. Каждому из двух возможных ответов («да» или «нет»)должны соответствовать указанные оценки (в смысле аддитивности оценок). В том случае если этого соответствия нет, то эксперт изменяет оценку Предположим, что эксперт признал: альтернатива a 1 предпочтительнее суммы всех остальных альтернатив. В этом случае должно выполняться неравенство оценок
Если это неравенство выполняется, то переходят к рассмотрению следующей альтернативы В том случае, когда эксперт признал, что альтернатива a 1 не предпочтительнее суммы всех остальных альтернатив, то для уточнения оценок она сравнивается по предпочтению с суммой оценок альтернатив а 2, а 3, … aN- 1(из суммы остальных исключается последняя альтернатива). Если эксперт утверждает, что альтернатива a 1 предпочтительнее суммы альтернатив а 2, а 3, … aN- 1, то проводится сравнение соответствующих оценок путем проверки выполнения условия
Процесс рассмотрения альтернативы a 1 продолжается до тех пор, пока она альтернатива а 1не окажется предпочтительнее суммы альтернатив а 2,…, ak (k ≥2). Тогда альтернатива а 1 исключается из рассмотрения. При этом исходная ее оценка может сохраниться или увеличиться. Затем подобная процедуре проводится с альтернативой а 2. Процесс заканчивается, когда будут рассмотрены все альтернативы и, если необходимо, откорректированы их оценки.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.186.72 (0.074 с.) |
 О 1
О 1  , (22)
, (22) , (24)
, (24)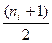 . (25)
. (25) , (26)
, (26) альтернатив и относительно каждой из них высказать свое предпочтение. Эксперт берет первую альтернативы и сравнивает ее со всеми другими, затем вторую и сравнивает ее со всеми другими и т.д. Результаты каждого высказанного предпочтения по каждой паре фиксируются. Правила фиксации предпочтения используют разные, например, такие:
альтернатив и относительно каждой из них высказать свое предпочтение. Эксперт берет первую альтернативы и сравнивает ее со всеми другими, затем вторую и сравнивает ее со всеми другими и т.д. Результаты каждого высказанного предпочтения по каждой паре фиксируются. Правила фиксации предпочтения используют разные, например, такие: предпочтительнее альтернативы
предпочтительнее альтернативы  , т.е.
, т.е.  =2;
=2; , которую называют матрицей предпочтений. Сумма оценок в строке
, которую называют матрицей предпочтений. Сумма оценок в строке  этой матрицы может рассматриваться как числовая оценка мнения эксперта. Та альтернатива
этой матрицы может рассматриваться как числовая оценка мнения эксперта. Та альтернатива  , у которой сумма
, у которой сумма  наибольшая по результатам экспертизы считается наиболее предпочтительной.
наибольшая по результатам экспертизы считается наиболее предпочтительной.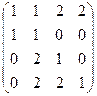
 .
. ) ставится в соответствие действительное неотрицательное число φ(аi);
) ставится в соответствие действительное неотрицательное число φ(аi); рассматриваемой альтернативы
рассматриваемой альтернативы  .
. . В противном случае величина
. В противном случае величина 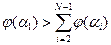 .
.


