
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка степени несогласованности и безразличия экспертов
Рассмотрим простейшие методы обработки данных, представленных в виде полученных от экспертов ответов на вопрос, который относится к вопросам открытого типа. Пусть, отвечая на поставленный вопрос, каждый из опрошенных m экспертов представил свой вариант ответа в виде ранжировки, включающей объекты, которые, по мнению эксперта, заслуживают того, чтобы быть отмечены. Пусть число объектов в ранжировке, полученной от i -го эксперта, равняется ni, (i = 1, …, m). Часть объектов при этом может быть упомянута сразу несколькими экспертами, тогда как другие объекты могут встретиться только в одной единственной ранжировке. Обозначим через n общее число всех объектов, которые были отмечены в ответе хотя бы одного из экспертов. Ясно, что будет справедливо нестрогое неравенство
n ≤
которое может обращаться в равенство лишь в том практически неосуществимом случае, когда каждый из экспертов перечислил в своей ранжировке такие объекты, которые не встречаются ни в одной из ранжировок, полученных от других экспертов. В ситуациях, встречаемых на практике, как правило, перечень ранжируемых объектов совпадает у всех экспертов на 70–80 %, и, следовательно, в (63) имеет место строгое неравенство. Постоим матрицу размерами m×n, элементами которой служат ранги Ri,j, которые были получены j -м объектом (j = 1, …, n) в ранжировке i -го эксперта (i = 1, …, m). Изначально в данной матрице будут наблюдаться «пробелы», поскольку не все n объектов были ранжированы каждым из экспертов. Для любого i = 1,…, m i -я строка матрицы, которая соответствует данному i -му эксперту, содержит число таких пробелов, равное, как легко заметить, n – ni. Чтобы заполнить эти пробелы, будем считать, что если тот или иной объект не был включен i -м экспертом в число ранжированных, то это означает, что эксперт оценивает качество данного объекта ниже, чем качество тех ni объектов, которые вошли в его ранжировку. Следовательно, каждому из (n – ni) объектов, не включенных в ранжировку, может быть выставлен одинаковый ранг, который ниже, чем ранги ni присутствующих в ней объектов. Рассуждая аналогичным образом для каждого из экспертов, мы получим следующее простое правило заполнения пробелов в матрице рангов Ri,j. Для того, чтобы все строки матрицы рангов после заполнения имеющихся в ней пробелов удовлетворяли условию (23), следует на место каждого из n – ni пробелов в i -й строке данной матрицы поставить ранг, равный
Дальнейшая обработка пополненной таким образом матрицы рангов состоит в следующем. Вычислим суммы Sj =
для каждого из имеющихся n объектов. Каждая такая сумма может принимать значения в пределах от своего минимально возможного значения Smin = m до Smax = m·n. Случай Sj = Smin означает, что все m экспертов единодушно поставили j -й объект на первое место. Если же оказалось, что Sj = Smax, то это тот редкий случай, когда, во-первых, у всех экспертов множества ранжированных объектов совпадают, а, во-вторых, j -й объект был признан всеми экспертами наихудшим. Общая сумма всех рангов, содержащихся в таблице, будет
Разделив (64) на общее число объектов n, можно найти S cp – «среднюю сумму рангов», приходящуюся на один оцениваемый объект
S cp =
Величина (67) может рассматриваться как своего рода граница, разделяющая все объекты на две категории: 1) качество которых «выше среднего»: Sj > S cp, 2) качество которых «ниже среднего»: Sj < S cp. Уже на этом этапе обработки экспертных оценок можно получить ответ на основной вопрос, который чаще всего ставится перед комитетом экспертов: какой объект является наиболее предпочтительным? Легко видеть, что таковым следует признать объект, который имеет наименьшую по сравнению с остальными объектами сумму (65). Однако такой формальный метод таит в себе опасность прийти к недостаточно обоснованному выводу. Прежде чем определять наилучший по формальным признакам объект, следует ответить на вопрос о том, имеет ли вообще данный комитет экспертов согласованную точку зрения. Ведь может оказаться, что мнения различных экспертов значительно отличаются друг от друга (например, одна часть экспертов придерживается взглядов одной научной школы, а другая – другой). В этом случае (назовем его случай несогласованности мнений экспертов) большинство из сумм рангов Sj будут несильно различаться между собой, поскольку высокие ранги, которые получил тот или иной объект у одной части комитета экспертов, будут компенсироваться низкими рангами, полученными им у других экспертов. Несогласованность может, в частности, проявляться и в том, что все ni намного меньше, чем n, т.е. заметная часть объектов, включенных в ранжировку одним экспертом, была вообще не упомянута большинством других экспертов.
Кроме несогласованности следует опасаться и случая безразличия комитета экспертов, т.е. когда эксперты не различают многие из объектов по уровню их качества. Этот случай проявляется в том, что большинство ранжировок содержат много связных рангов. Итак, требуется критерий, позволяющий проверить, имеет ли место в данном конкретном случае несогласованность или безразличие, или же результаты опроса позволяют выявить согласованную точку зрения комитета экспертов. По аналогии с дисперсией, которая, как известно, служит показателем разброса значений случайной величины, рассмотрим сумму
В силу приведенных выше соображений малые значения (87) будут указывать на отсутствие у экспертов общего согласованного мнения. С помощью суммы (68) может быть найден так называемый коэффициент конкордации W, который служит в качестве критерия согласованности мнений комитета экспертов [117]:
где Ti - поправочные коэффициенты
необходимые для расчета коэффициента конкордации; ki – число различных уровней, выделенных i -м экспертом; ni,l – число элементов, которые i -м экспертом были отнесены к l -му уровню (l = 1,…, ki). Можно показать, что каковы бы ни были результаты ранжировки значение коэффициента конкордации всегда лежит в пределах 0 ≤ W ≤ 1. При этом случай W = 0 соответствует полной несогласованности мнений экспертов или их безразличию, так как при этом все Sj = S cp. Напротив, чем больше значение W, тем выше согласованность мнений комитета экспертов. При W = 1 имеет место полное единодушие экспертов, которые все одинаковым образом упорядочивают данное множество объектов. Большие значения коэффициента конкордации W указывают на согласованность мнений комитета экспертов. Остается ответить на вопрос о том, где та граница, которая отделяет «большие» значения W от «маленьких». Для ответа на этот вопрос воспользуемся той же моделью, которая уже применялась для ранговых коэффициентов корреляции. Предположим, что любые результаты ранжировки, получаемые от m экспертов равновероятны, то есть имеет место полная несогласованность мнений. В этих условиях оказывается, что величина m (n – 1) W подчиняется распределению хи-квадрат с (n – 1) степенями свободы. Следовательно, если для выбранного уровня значимости α выполнено неравенство χ2 расчет = m (n – 1) W > χ2 табл, (71)
где χ2 табл – α-процентная точка распределения хи-квадрат, то гипотезу об отсутствии согласованности следует отвергнуть. Этот вывод принято интерпретировать как наличие согласованного мнения у данного комитета экспертов. На практике, если условие (71) выполняется, то принимается окончательное решение, согласно которому оцениваемое качество объектов упорядочено в соответствии с упорядочением сумм Sj их рангов. Если же коэффициент конкордации мал, так что неравенство (71) не выполнено, то рекомендуется, прежде всего, попытаться добиться большей однородности комитета экспертов, тем самым повысив его согласованность. В самом деле, возможно, что низкая степень согласованности вызвана мнением одного-двух экспертов, чья точка зрения (или чьи критерии оценивания) резко отличаются от остальных. Тогда, если исключить этих одного-двух экспертов, вполне возможно, что результат обработки оценок остальных экспертов приведет к согласованному результату.
Чтобы определить экспертов, которых, возможно, следует исключить (их называют диссидентами), поступают следующим образом. Пусть R (Sj) обозначает ранг j –го объекта в итоговом упорядочении: R (Sj) = 1 для объекта с минимальной суммой Sj и т.д., …, R (Sj) = n для объекта, имеющего максимальную сумму рангов. Обозначим
∆ Ri,j = │ Ri,j – R (Sj) │ (72)
- абсолютную величину разности между тем рангом, который i -й эксперт присвоил j –му объекту, и рангом, который этот же объект получил в итоговой ранжировке. Ясно, что сумма
будет указывать на то, в какой мере оценки i -го эксперта отличаются от общей точки зрения всего комитета экспертов в целом. Таким образом, если (71) не выполняется, то из числа экспертов следует в первую очередь исключить того, у которого сумма (73) максимальна. Далее, с учетом произведенного сокращения числа экспертов следует пересчитать заново значения величин (65), (67) и коэффициента конкордации (69). Если вновь вычисленное значение W будет удовлетворять (71), то цель достигнута: новый (сокращенный) состав экспертов имеет согласованное мнение, которое и может быть принято за окончательное решение. Если же по-прежнему (71) не выполнено, то есть согласованное мнение не выражено, то процесс сокращения комитета может быть повторен еще столько раз, сколько это необходимо. Если конечная цель обработки данных экспертного опроса ограничена лишь определением наиболее важного (качественного) объекта, то описанный алгоритм вполне приемлем, разумеется, если искомое согласованное мнение будет в конечном итоге получено. Однако поставленная конечная цель может быть шире, например, она может состоять в выявлении как можно большего числа оригинальных мнений, поскольку нередко именно «диссиденты» способны предложить нестандартный подход к оцениваемой ситуации, и поэтому просто проигнорировать мнение меньшинства было бы неразумно. В таких случаях требуется более углубленный анализ содержания задачи и менее формальный подход к ее решению. Однако и здесь, при наличии явно выраженного разнообразия в подходах различных групп экспертов, будет весьма полезным вычислить ранговые коэффициенты корреляции между ранжировками, полученными от разных экспертов, с тем, чтобы сделать более наглядной структуру комитета экспертов, т. е. выявить группировки экспертов, выражающих различные подходы к оцениваемым показателям.
ЗАКЛЮЧЕНИЕ
Широко известно изречение И.Канта: «Учение о природе будет содержать науку в собственном смысле лишь в той мере, в какой может быть применена в нем математика» [118]. В чем суть этой мысли? Почему математика, как мир идей, сконструированный воображением людей, и объективные законы природы находятся в столь тесной связи? Дело в том, что и законы природы и математические идеи обладают одинаковым фундаментальным свойством: на них не действует время. Законы природы существуют всегда, хотя человек может знать о них или нет. Также и математические объекты обладают «вневременным бытием». Прямая линия, квадрат, окружность и т.д. не могут быть физически изготовлены, они продукт мысли. Однако, в отличие от других мыслей они обладают тождественностью самим себе (именно в этом смысле они вечны) [119]. Таким образом, в тех случаях, когда при решении вопросов удается воспользоваться математикой, в смысле использования математических моделей, мы имеем основания для уверенности в том, что найденный ответ верен. Казалось бы, все ясно: требуется сформировать математическую модель объекта исследования и провести на ней математический эксперимент. В чем же тогда состоят встречающиеся на этом пути трудности? Конечно, требуются знания математики и неукоснительное соблюдение условий применимости математических процедур. Но проблема гораздо глубже. Необходимо осознать диалектическую связь между наукой и познаваемым миром. Окружающий нас мир во всех своих проявлениях исключительно сложен и разнообразен. Однако, наука в целом, а математика в частности, (крайне бедные по сравнению с природой) обеспечивают достижение существенных успехов в познании окружающего нас мира. В частности, располагая математическими моделями, имеется возможность точного расчета, описания и предсказания явлений, которые часто поражают своей необычностью [120]. Это противоречие объясняется тем, что наука, используя весьма бедные и грубые средства, выхватывает из действительности лишь отдельные группы проявления качества объекта исследования, игнорируя все остальное. Иначе говоря, в борьбе за точность и универсальность результатов исследований приходится платить сокращением области их применимости. Между тем возможности науки, и в первую очередь за счет успехов математики и информатики, постоянно расширяются, в чем состоят основные преимущество и перспективы научной деятельности.
По мере развития цивилизации приходится решать все более сложные проблемы, побуждающие разрабатывать новые подходы, теории и модели. Среди них разработка теории систем и системного анализа - реакция на потребность рассмотрения объектов, как систем, обеспечивающая очередной шаг в расширении области применения науки.
Научные положения теории систем имеют большую общность, соизмеримую с современными философскими воззрениями. Ее отличительные черты характеризуются не только в масштабностью, а дают и чисто практический результат во всех сферах человеческой деятельности. В этом плане теория систем претендует на место натурфилософии 21 века.
Представленная работа, отражая мнение и взгляды ее автора и авторов использованных источников, преследует цель донести их до читателя и способствовать расширению их кругозора относительно одной из перспективных тенденций современной науки.
БИБЛИОГРАФИЯ
1. Авдеева З.К. и др. Когнитивный подход в управлении // Проблемы управления – 2007. -№3. – С. 2-8. 2. Акофф Р.Теория управления. Менеджмент. Часть 1. Общая теория систем - основа теории управления. /ГИУСТ БГУ, 2007. 3. Антонов И.В., Воронов М.В. Метод построения онтологии предметной области // Вестник Санкт-Петербургского государственного университета технологии и дизайна. - Серия 1. Естественные и технические науки. - 2. - 2010. - С. 28-32. 4. Асланов М.А. и др. Системный анализ и принятие решений в деятельности учреждений реального сектора экономики, связи и транспорта. / М. ЗАО «Издательство «Экономика», 2009. 5. Баринов Ю.Г. Разработка управленческих решений. /Псков: Изд-во СПГПУ, 2003. 6. Беляев М.И. Основы теории иерархии. 2005. [Электронный ресурс]. — Режим доступа: http://milogiya.narod.ru/edinpole3.htm. 7. Берталанфи Л. Общая теория систем. /М.: Системное моделирование, 1969. 8. Бешенков С. А. Информация и информационные процессы. //Информатика и образование. 1998. № 6 - 8. 9. Большаков Б.Е., Кузнецов О.Л., Кузнецов П.Г. Система природа – общество – человек. – Международный университет «Дубна», 2000. 10. Васильев К.К., Служивый М.Н. Математическое моделирование систем свзязи - Ульяновск: УлГТУ, 2008 г. 11. Вертешев С.М., Поляков А.О. От фон Неймановского компьютера к метамашине. /Псков: Издательство ППИ, 2007. 12. Вилкас Э.И., МайминесЕ.З. Решения: теория, информация, модели. –М.: Радио и связь, 1981. 13. Волкова В.Н. Основы теории систем и системного анализа. /СПб: Издательство СПбГУТД, 2003. 14. Воронов М.В. Нечеткие множества в моделях организационного управления. /Учебное пособие. – Л.:ВМА, 1988. 15. Воронов М.В. Разработка вполне гибких открытых информационных систем. //Труды 4 Международной конференции Новые информационные технологии. Минск -2000. 5-7 декабря, 2000. С.20-28. 16. Воронов М.В., Мещерякова Г.П. Математика для гуманитарных факультетов /Учебник. – Ростов н/Д: Феникс, 2002. 17. Воронов М.В., Пименов В.И, Суздалов Е.Г. Прикладная математика. /Учебное пособие. –СПбГУТД, СПб., 2003. 18. Воронов М.В. Конструктивно-имитационное моделирование слабоструктурированных систем. //Известия МАН ВШ, №4(42) 2007г. С.156-165. 19. Воронов М.В., Захаров В.К. Основные математические понятия. Часть 1. /Псков: Издательство ППМ, 2008. 20. Гайдес М.А. Общая теория систем (системы и системный анализ). /Винница, «Глобус-Пресс»», 2005. 21. Грекул В.И. Проектирование информационных систем. //Интернет университет информационных технологий. [Электронный ресурс]. — Режим доступа: http://www.intuit.ru/department/se/devis/9/. 22. Губарь Ю.В. Введение в математическое программирование. Интернет университет. Электронный ресурс: Электронный ресурс: http://www.intuit.ru/department/mathematics/mathprog/1/09.07.2007 23. Дроздов Н.Д. Постановка задачи в прикладных математических исследованиях. –Тверь: Издательство Тверского государственного университета, 2006. 24. Дулов В.Г., Цибаров В.А. Концепция современного естествознания:Электронное учебное пособие -- СПб: НИИ математики и механики СПбГУ, 2002. [Электронный ресурс]. — Режим доступа: http://www.math.spbu.ru/ru/Archive/Courses/tsib/dul_tsib/node1.html 25. Живицкая Е. Н. «Системный анализ и проектирование». [Электронный ресурс]. — Режим доступа: http://victor-safronov.narod.ru/systems-analysis/lectures/zhivickaya.html.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.059 с.) |
 , (63)
, (63) . (64)
. (64) (65)
(65)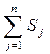 =
=  =
=  =
=  =
=  . (66)
. (66) . (67)
. (67) . (68)
. (68) , (69)
, (69) , (70)
, (70) (73)
(73)


