
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл с однократным дросселированиемСодержание книги
Поиск на нашем сайте
ЦИКЛ БЕЗ РЕГЕНЕРАЦИИ Рассмотрим цикл с однократным дросселированием без регенерации, т.е. будем полагать, что дросселируется сжатый газ от температуры окружающей среды внутри кривой инверсии (при этом будет наблюдаться охлаждение). На рисунке 3.1 дано изображение рассматриваемого цикла: 1 – 2 - изотермическое сжатие; 2 – 3 - дросселирование; 3 – 1 – изобарный нагрев. В действительности процесс 1 – 2 – это совокупность двух процессов: 1 – 2* - адиабатное сжатие и 2* - 2 – изобарное охлаждение. В реальных установках используется многоступенчатое сжатие с промежуточным охлаждением. Для рассматриваемого цикла величина холодопроизводительности q0 записывается в виде
q0 = i1 – i2 =D iT (3.1)
Холодопроизводительность цикла с однократным дросселированием без регенерации определяется величиной интегрального изотермического дроссель-эффекта. Из рассмотрения цикла видно, что параметры лишь двух точек 1 и 2 определяют энергетические характеристики цикла. Точка 1 чаще всего определяется параметрами окружающей среды и поэтому является как бы фиксированной. Таким образом,фактически, лишь положением точки 2 определяются энергетические характеристики цикла. Положение точки 2, в свою очередь, определяется Т окр.ср. и давлением Р2. Следовательно, лишь одна величина -давление сжатия Р2 влияет на энергетические характери
стики цикла.
Рис. 3.1. Цикл с однократным дросселирование без регенерации
При заданной температуре Т окр.ср. максимальное давление, при котором холодопроизводительность цикла будет максимальной, соответствует давлению инверсии Ринв., которое определяется изобарой, проходящей через точку касания изоэнтальпы и изотермы окружающей среды. Например, для воздуха при Т окр.ср. = 300 К значение Ринв. = 400 бар. На приводимом рисунке видно, что с ростом давления сжатия Р2 холодопроизводительность цикла возрастает, если давление сжатия, разумеется, не превышает давления инверсии. Таким образом, в рассматриваемом цикле холодопроизводительность растёт с ростом давления сжатия Р2 до тех пор, пока оно не превышает давления инверсии Ринв. Для криогенных веществ, у которых максимальная температура инверсии меньше температуры окружающей среды (например, для гелия, неона, водорода) невозможно получить холод в цикле с однократным дросселированием, т.к. при дросселировании от температуры окружающей среды будет наблюдаться нагрев, а не охлаждение.
Если в качестве рабочего тела для этого цикла использовать идеальный газ, то холодопроизводительность q0 = 0 (точка 3 совпадает с точкой 1). Напомним, что для идеального газа ai = 0, а следовательно, aT = 0 и DiT = 0. Выражения для работы и холодильного коэффициента имеют вид
Вместо точного выражения для работы, приведенного выше,часто используют приближенное выражение, полагая, что сжимаемый газ при температуре окружающей среды следует законам идеального газа
l = R Tокр.ср. ln (P2/P1) (3.3)
Ошибка, возникающая при этом, например, для воздуха составляет около 10%, если Р2 = 200 бар. C ростом Р2 увеличивается холодопроизводительность q0 и работа цикла l. Вблизи кривой инверсии, однако, рост холодопроизводительности q0 замедляется. Работа цикла l c ростом Р2 увеличивается. Анализ показывает, что максимум холодильного коэффициента лежит при давлении более низком, чем давление, соответствующее максимуму холодопроизводительности. Рассмотрим влияние регенерации на энергетические характеристики цикла с однократным дросселированием. ЦИКЛ С РЕГЕНЕРАЦИЕЙ Рассмотрим цикл с однократным дросселированием и регенерацией (рис. 3.2). Этот цикл был первым криогенным циклом, который нашёл практическое применение в технике. Цикл с регенерацией (в виде отдельной ступени с дросселированием) является элементом большей части современных криогенных установок. Впервые цикл реализовали в 1895 г. независимо друг от друга Линде в Германии и Хэмпсон в Англии. Рассмотрим контур, выделенный пунктиром, на рис. 3.2. Запишем энергетический баланс для выделенного контура
Рис. 3.2. Цикл с однократным дросселированием и регенерацией 1 – 2 – изотермическое сжатие; 2 – 3 – изобарное охлаждение прямого потока обратным; 3 – 4 – дросселирование; 4 – 5 – процесс подвода тепла (в рефрижераторных циклах); 5 – 1 – изобарный подогрев обратного потока.
Из полученного выражения следует, что и в цикле с регенерацией (как и в цикле без регенерации) холодопроизводительность цикла q0 определяется величиной интегрального изотермического дроссель-эффекта. Следовательно, включение регенеративного теплообменника, не изменив численно количество получаемого холода q0, понизило его температуру, т.е. сделало холод более ценным. Используя очевидное выражение для теплового баланса регенеративного теплообменника, можно привести и иную запись для холодопроизводительности цикла
Последнее выражение, где холодопроизводительность определяется положением точек 5 и 4 рассматриваемого цикла, более привычно для выражения холодопроизводительности при рассмотрении циклов установок умеренного холода. По сравнению с выражением (3.4) оно менее информативно, так как прямо не указывает на источник производства холода. Приведём также выражения для работы и холодильного коэффициента
Перепишем тепловой баланс для регенеративного теплообменника, выразив разность энтальпий потоков через величины соответствующих темлоёмкостей (прямого и обратного потоков) и разностей температур на концах теплообменика. Исходя из того, что изобарная теплоёмкость растёт с ростом давления, можно заключить, что Ср2 большая величина (условно " б "), а Ср1 малая величина (условно " м "). Отсюда, как следствие, получаем неравенства, приведенные в (3.7)
Уменьшение необратимости процесса дросселирования, таким образом, связано с тем, что при низких температурах изоэнтальпы идут круто, приближаясь к адиабатам; при высоких
температурах, наоборот, изоэнтальпы идут полого, приближаясь к изотермам, поэтому процесс 3 – 4 (рис. 3.2) более обратим, чем процесс 2 – 3 (рис. 3.1).
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.009 с.) |



 (3.2)
(3.2)
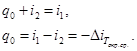 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7)


