
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №1. Исследование линейных стационарных системСтр 1 из 7Следующая ⇒
Содержание
Введение Математическое моделирование - это средство для изучения процессов, протекающих в различных системах и устройствах без их создания «в натуре». Существует два принципиально различных подхода к построению математических моделей. Первый подход основан на выборе моделей с учетом основных физико-химических закономерностей, определяющих течение исследуемого процесса. Такие модели называются аналитическими моделями процесса. Моделирование в этом случае основано на ограниченности числа фундаментальных законов природы и принципе подобия, означающем, что явления различной физической природы могут описываться одинаковыми математическими зависимостями. Аналитические методы определения характеристик объектов регулирования основаны на составлении их дифференциальных уравнений, базирующемся на использовании основных физических законов: сохранения массы, энергии и количества движения. Как правило, этим методом удается получить нелинейное уравнение объекта, аналитическое решение которого в общем случае не может быть получено. Следующим шагом является линеаризация полученного уравнения, то есть переход к линейной математической модели объекта. Линеаризация обычно проводится путем разложения нелинейных зависимостей в ряд Тейлора в окрестности исходного стационарного режима с сохранением только линейных частей разложения и последующим вычитанием уравнений статики. Полученная таким образом линейная модель объекта справедлива лишь при малых отклонениях от исходного стационарного режима. Второй подход базируется на концепции "черного ящика", то есть постулируется, что внутренняя структура объекта неизвестна, да и не должна интересовать исследователя. Вся информация получается только в результате наблюдений за объектом при пассивном и активном эксперименте. Полученные таким образом модели называются эмпирическими (экспериментальными). При построении эмпирических моделей используются реализации входных и выходных переменных объекта. Задачи восстановления таких моделей изучаются в теории идентификации. Экспериментальные методы определения динамических характеристик делятся на три основные группы: прямые методы идентификации, параметрическая и непараметрическая идентификации.
Предлагаемые методические указания к лабораторным работам по дисциплине «Моделирование и идентификации объектов управления» включают 7 работ. Для выполнения этих работ (кроме работы 5) используются различные инструментарии программной системы MatLab. Эта система выгодно выделяется среди систем компьютерного моделирования. Она является одной из старейших систем автоматизации математических расчетов и построена на расширенном представлении и применении матричных операций, что нашло отражение в названии системы - MATrix LABoratory(матричная лаборатория). Отметим те средства системы, которые будут использоваться для выполнения лабораторных работ. Любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений (в командном режиме), то есть без подготовки программы. Это превращает MatLab в необычайно мощный научный калькулятор, который способен производить не только обычные для калькуляторов вычисления, но и операции с векторами, матрицами, комплексными числами, рядами и полиномами. Причем работа в этом режиме носит диалоговый характер. Командное окно часто используется и при работе в различных пакетах системы MatLab. Например, данные между отдельными пакетами не передаются напрямую, а только лишь через командное окно. Несмотря на значительные возможности работы в режиме калькулятора, сложные вычисления требуют оформления их в виде программ. Для использования процедур пользователь создает М-файл в специальном окне редактора программ. Рекомендуется выполнить упражнения, приведенные в [6], п.п.1 и 2, чтобы освоить основные приемы программирования и работы в командном окне системы MatLab. В лабораторной работе 1 для создания и анализа моделей линейных стационарных систем используется командное окно системы и пакет ControlSystem Toolbox. Пакет Control Toolbox предоставляет широкий набор процедур, осуществляющих анализ системы автоматического управления с самых различных точек зрения и, прежде всего, определение откликов системы на внешние воздействия, как во временной, так и в частотной области. Популярности системы MatLab способствует ее мощное расширение Simulink, предоставляющее пользователю удобные и простые средства, в том числе визуального объектно-ориентированного программирования, для блочного моделирования линейных и нелинейных динамических систем. В лабораторных работах 2 и 3 модели исследуемых процессов реализуются в виде блок-диаграмм пакета Simulink, и исследование модели проводится в визуальном режиме. Этот пакет также используется в лабораторной работе 4 для идентификации объекта графическим методом. Моделирование систем и устройств, поведение которых зависит от внешних событий, в системе MatLab + Simulink реализуется с помощью специального расширения Stateflow. Этот пакет используется при выполнении лабораторной работы 3.
В лабораторной работе 5 идентификация объекта с помощью частотной характеристики проводится в среде программы, разработанной на кафедре «Инженерная кибернетика». Для параметрической идентификации систем (лабораторная работа 6) используется графическая оболочка ident программного продукта MatLab. Задачи непараметрической идентификации систем рассмотрены в лабораторной работе 7. Для численного решения задачи непараметрической идентификации используется командное окно системы. Для аппроксимации дискретных значений искомой импульсной переходной функции используется пакет подгонки кривых Curve Fitting Toolbox. Динамических объектов
Цель работы: освоить методы непараметрической идентификации систем, и пакет подгонки кривых Curve Fitting Toolbox системы MatLab.
7.1 Постановка задачи Непараметрическая модель определяется в общем случае непрерывной функцией, но она может быть задана точками или в виде разложения в ряд по какой-либо системе функций. Специфика линейного динамического объекта однозначно определяется его реакцией на единичное импульсное воздействие. Это обстоятельство и лежит в основе определения непараметрической модели, которая характеризуется импульсной (весовой) переходной функцией. При идентификации линейного стационарного динамического объекта статистическими методами весовая функция определяется из уравнения Винера-Хопфа Один из способов его решения – численный. Суть численного метода заключается в возможности представления этого уравнения системой линейных алгебраических уравнений. Для этого заменим интеграл конечной суммой здесь ∆ - интервал дискретизации; n∆ - дискретное время; N – количество интервалов. Это уравнение справедливо для τ = ∆, …, N∆. Подставляя в это уравнение N значений τ, получим систему из N уравнений. Это система для определения значений импульсной переходной функции в дискретные моменты ∆, …, N∆. Итак, получаем систему уравнений Ag = b (7.2) где А – квадратная матрица; b = [b1, b2,…,bm]T - вектор-столбец с компонентами bi=Ryx(τ)/∆, i = 1,...,m; g = [g1, g2,…,gm]T – вектор-столбец искомых значений импульсной переходной функции. Решение этой системы позволяет определить дискретные значения ординат весовой функции g(τ) в точках t, 2t,…, mt. Эти решения получаются с большими погрешностями, так как вместо истинных значений корреляционных функций используются их оценки, а сама система плохо обусловлена. Хотя полученные значения импульсных переходных функций имеют малую среднеквадратичную ошибку, близкую к минимуму, ценность их невелика, так как эти функции не соответствуют физическому смыслу процессов в объекте. Физический смысл имеют гладкие решения. Поэтому используются различные процедуры сглаживания импульсной переходной функции.
7.2 Аппроксимация дискретной импульсной переходной функции Для получения сглаженных импульсных переходных функций, используется процедура приближения значений этой функции с помощью какого-либо аппроксимирующего полинома. Чаще всего используется разложение по какой-либо системе ортогональных полиномов где φk(t) – заданная система функции; N – порядок разложения; ak – коэффициенты ряда, которые вычисляются по формуле Функции разложения выбираются таким образом, чтобы достичь хорошего приближения при небольшом их числе. Целесообразно выбирать ортогональные функции, преобразуемые по Лапласу (полиномы Чебышева, Лагерра, Лежандра).
7.3 Пакет подгонки кривых Curve Fitting Toolbox Пакет подгонки кривых Curve Fitting Toolbox обеспечивает подгонку кривых с использованием метода наименьших квадратов. Работу с пакетом надо начинать с загрузки данных. Данные могут быть сформированы в командном окне системы в соответствующих векторах. Основное окно пакета Curve Fitting Tool открывается командой cftool (в командном окне MatLab). Вначале оно имеет пустое окно графики и 4 кнопки над ним: Data... - загрузка данных; Fitting... - выполнение подгонки; Ploting... - графическая визуализация подгонки; Analysis... - анализ результатов подгонки. Импорт данных. Обычно работа с окном Curve Fitting Tool начинается с уточнения типа загружаемых данных, для чего необходимо активизировать кнопку Data.... Это ведет к появлению окна импорта данных Data. В этом окне с помощью соответствующих вкладок можно установить тип множеств данных, просмотреть их, скорректировать и сгладить. Нажатие кнопки Apply и закрытие окна приводит к загрузке скорректированных данных в основное окно Curve Fitting Tool. В результате точки данных появляются в поле графики этого окна. Выполнение подгонки заданного типа. Выбор кнопок Fitting/New Fit позволяет начать процедуру подгонки. Открывающийся список Type of fit позволяет установить любой из следующих типов подгонки (регрессии): - Custom equations — функция регрессии, задаваемая пользователем; - Exponential — экспоненциальная репрессия; - Fourier — приближение рядом Фурье; - Gaussian — приближение кривой гауссиана; - interpolant — интерполяция с выбором метода; - Polynomial — полиномиальная регрессия; - Power — степенная регрессия; - Rational — регрессия рациональной функцией с выбором ее числителя и знаменателя; - Smoothing Spline — регрессия сглаживающими сплайнами; - Sum of Sin Func — регрессия суммой синусоидальных функций; - Weibull — регрессия кривой Вейбулла. Как видно из этого перечисления, представлен внушительный набор возможных видов приближений. Особенно важно, что среди них есть возможность задания пользователем функции регрессии любого вида, разумеется, на основе встроенных функций MatLab.
Если нажать кнопку Fit Options... окна подгонки Fitting, можно задать ряда опций подгонки. В окне опций подгонки возможна установка различных алгоритмов подгонки, пределов изменения производных, максимального значения функции и начальных значений параметров регрессии. Все эти величины существенно влияют на сходимость и скорость подгонки. Графическая визуализация регрессии. Кнопка Plotting... окна Curve Fitting Tool открывает окно установок графики. Анализрезультатов регрессии. Важным этапом приближения является анализ результатов. Он проводится при активизации кнопки Analysis... окна Curve Fitting Tool. При этом открывается окно анализа Analysis. В левой части окна имеется ряд опций анализа: выполнения вычислений, вывода графиков производных и интеграла для функции регрессии и др. Нужные опции задаются установкой знака птички у их названия. После этого нажатие кнопки Apply формирует таблицу результатов анализа сверху окна и выводит окно с графическим представлением результатов анализа. Основным критерием выбора кривой регрессии является минимум погрешности Residuals в заданном диапазоне изменения аргумента, отсутствие резких выбросов кривой погрешности на краях этого диапазона или в отдельных его областях и т. д. Нередко важным является соответствие кривой регрессии возможному закону расположения точек исходных данных. Рекомендуется опробовать несколько кривых регрессии для заданного набора точек.
7.4 Задание на лабораторную работу Зарегистрированы входные и выходные переменные исследуемого объекта в течение определенного интервала времени. По результатам этих измерений вычислены автокорреляционная и взаимнокорреляционная функции (см. таблицу вариантов). Требуется определить численным методом из уравнения Винера-Хопфа импульсную переходную функцию. Затем полученные дискретные значения этой функции следует аппроксимировать полиномами различных порядков и выбрать наилучшую степень аппроксимации.
7.5 Порядок выполнения работы 7.5.1 Записать систему линейных алгебраических уравнений (7.2) для своего варианта. 7.5.2 Решить систему (7.2), используя командное окно системы MatLab: - введите компоненты матрицы A и вектора b в командное окно системы; - проверьте существование решения системы (7.2), набрав в командной строке det(A); как известно, для существования решения необходимо, чтобы det(A) ≠ 0; - получите решение системы, применив процедуру g = b*inv(A). 7.5.3 Используя пакет Curve Fitting Tool, выполните аппроксимацию полученных дискретных значений полиномами различных порядков. Для задания своего уравнения регрессии в списке видов регрессии надо выбрать позицию Custom equations. Это приводит к появлению окна задания регрессии Create Custom Equations. Это окно имеет две вкладки. На первой вкладке Linear Equations можно задать параметры уравнения, линейного относительно коэффициентов регрессии. Заметим, что сама зависимость при этом может быть нелинейной. На другой вкладке General Equations можно установить произвольное нелинейное уравнение регрессии, т. е. осуществить нелинейную регрессию. 7.5.4 Завершив подгонку, выведите графики исходных точек, кривых приближения и погрешностей. 7.5.5 Выберите полином, который наилучшим образом аппроксимирует импульсную весовую функцию. 7.6 Требования к отчету Отчет по работе должен содержать: - систему алгебраических уравнений для определения дискретных значений импульсной переходной функции; - результат решения этой системы; - результаты подгонки; - обоснованный выбор наилучшего аппроксимирующего полинома. 7.7 Варианты заданий
7.8 Контрольные вопросы 7.8.1 В чем суть непараметрической идентификации? 7.8.2 Какие объекты описывает уравнение Винера-Хопфа, 7.8.3 Почему возможно представить уравнение Винера-Хопфа системой алгебраических уравнений? 7.8.4 Что такое аппроксимация функции? 7.8.5 Объясните назначение пакета Curve Fitting Tool. 7.8.6 Какая из функций дает лучшие результаты приближения?
Список литературы 1. Дейч А.М Методы идентификации динамических объектов.- М.: Энергия, 1979. 2. Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высшая школа, 1991. 3. Лазарев Ю. MatLab 5.x. – Киев: «Ирина», BHV, 2000. 4. Дьяконов В. П. MatLab 6/6.1/6.5 + Simulink 4/5. Основы применения. – М.: Солон-ПРЕСС, 2004. 5. Matlab 6.5 SP1/7.06. Simulink 5/6 в математике и моделировании. – М.: СОЛОН-Пресс, 2005. 6. Ибраева Л.К.Основные приемы работы в среде Matlab. Методический практикум. – Алматы: АИЭС, 2004. 7. www.exponenta.ru 8. www.matlab.ru
Доп.план 2007 г., поз. 38
Лида Куандыковна Ибраева
Содержание
Введение Математическое моделирование - это средство для изучения процессов, протекающих в различных системах и устройствах без их создания «в натуре». Существует два принципиально различных подхода к построению математических моделей. Первый подход основан на выборе моделей с учетом основных физико-химических закономерностей, определяющих течение исследуемого процесса. Такие модели называются аналитическими моделями процесса. Моделирование в этом случае основано на ограниченности числа фундаментальных законов природы и принципе подобия, означающем, что явления различной физической природы могут описываться одинаковыми математическими зависимостями. Аналитические методы определения характеристик объектов регулирования основаны на составлении их дифференциальных уравнений, базирующемся на использовании основных физических законов: сохранения массы, энергии и количества движения. Как правило, этим методом удается получить нелинейное уравнение объекта, аналитическое решение которого в общем случае не может быть получено. Следующим шагом является линеаризация полученного уравнения, то есть переход к линейной математической модели объекта. Линеаризация обычно проводится путем разложения нелинейных зависимостей в ряд Тейлора в окрестности исходного стационарного режима с сохранением только линейных частей разложения и последующим вычитанием уравнений статики. Полученная таким образом линейная модель объекта справедлива лишь при малых отклонениях от исходного стационарного режима. Второй подход базируется на концепции "черного ящика", то есть постулируется, что внутренняя структура объекта неизвестна, да и не должна интересовать исследователя. Вся информация получается только в результате наблюдений за объектом при пассивном и активном эксперименте. Полученные таким образом модели называются эмпирическими (экспериментальными). При построении эмпирических моделей используются реализации входных и выходных переменных объекта. Задачи восстановления таких моделей изучаются в теории идентификации. Экспериментальные методы определения динамических характеристик делятся на три основные группы: прямые методы идентификации, параметрическая и непараметрическая идентификации. Предлагаемые методические указания к лабораторным работам по дисциплине «Моделирование и идентификации объектов управления» включают 7 работ. Для выполнения этих работ (кроме работы 5) используются различные инструментарии программной системы MatLab. Эта система выгодно выделяется среди систем компьютерного моделирования. Она является одной из старейших систем автоматизации математических расчетов и построена на расширенном представлении и применении матричных операций, что нашло отражение в названии системы - MATrix LABoratory(матричная лаборатория). Отметим те средства системы, которые будут использоваться для выполнения лабораторных работ. Любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений (в командном режиме), то есть без подготовки программы. Это превращает MatLab в необычайно мощный научный калькулятор, который способен производить не только обычные для калькуляторов вычисления, но и операции с векторами, матрицами, комплексными числами, рядами и полиномами. Причем работа в этом режиме носит диалоговый характер. Командное окно часто используется и при работе в различных пакетах системы MatLab. Например, данные между отдельными пакетами не передаются напрямую, а только лишь через командное окно. Несмотря на значительные возможности работы в режиме калькулятора, сложные вычисления требуют оформления их в виде программ. Для использования процедур пользователь создает М-файл в специальном окне редактора программ. Рекомендуется выполнить упражнения, приведенные в [6], п.п.1 и 2, чтобы освоить основные приемы программирования и работы в командном окне системы MatLab. В лабораторной работе 1 для создания и анализа моделей линейных стационарных систем используется командное окно системы и пакет ControlSystem Toolbox. Пакет Control Toolbox предоставляет широкий набор процедур, осуществляющих анализ системы автоматического управления с самых различных точек зрения и, прежде всего, определение откликов системы на внешние воздействия, как во временной, так и в частотной области. Популярности системы MatLab способствует ее мощное расширение Simulink, предоставляющее пользователю удобные и простые средства, в том числе визуального объектно-ориентированного программирования, для блочного моделирования линейных и нелинейных динамических систем. В лабораторных работах 2 и 3 модели исследуемых процессов реализуются в виде блок-диаграмм пакета Simulink, и исследование модели проводится в визуальном режиме. Этот пакет также используется в лабораторной работе 4 для идентификации объекта графическим методом. Моделирование систем и устройств, поведение которых зависит от внешних событий, в системе MatLab + Simulink реализуется с помощью специального расширения Stateflow. Этот пакет используется при выполнении лабораторной работы 3. В лабораторной работе 5 идентификация объекта с помощью частотной характеристики проводится в среде программы, разработанной на кафедре «Инженерная кибернетика». Для параметрической идентификации систем (лабораторная работа 6) используется графическая оболочка ident программного продукта MatLab. Задачи непараметрической идентификации систем рассмотрены в лабораторной работе 7. Для численного решения задачи непараметрической идентификации используется командное окно системы. Для аппроксимации дискретных значений искомой импульсной переходной функции используется пакет подгонки кривых Curve Fitting Toolbox. Лабораторная работа №1. Исследование линейных стационарных систем
Цель работы: создание моделей динамических систем в командном окне MatLab; анализ моделей средствами пакета Control System Toolbox.
1.1 Основные виды моделей линейных динамических объектов В целом ряде случаев реакция линейной стационарной системы на то или иное достаточно простое воздействие определяется ее теоретическими характеристиками. Основными из них являются: - передаточная функция W(p) (определяется с помощью преобразования Лапласа L{∙}); - импульсная характеристика g(t) – реакция предварительно невозмущенного объекта на входной сигнал в виде δ-функции. При нулевых начальных условиях связь между выходным и входным сигналами описывается интегралом свертки - переходная функция h(t) – реакция предварительно невозмущенного объекта на входной сигнал в виде единичного скачка. Из теории управления известны следующие соотношения между этими характеристиками L{w(t)} = W(p), g(t)= h’(t), - частотные характеристики объекта, которые определяются комплексным коэффициентом передачи W(jω)= W(p) | p=jω. Под моделью будем понимать информацию о наиболее существенных характеристиках объекта, выраженную в той или иной форме. Приведем основные виды моделей линейных непрерывных стационарных динамических объектов. 1. Дифференциальные уравнения. Наиболее универсальная модель, основанная на дифференциальных уравнениях, описывается выражением где na - порядок модели (na > nb); ai и bj - постоянные коэффициенты (параметры модели); u(j)(t) и y(i)(t) - производные соответственно входного и выходного сигналов. 2. Уравнения переменных состояния. При выборе n координат системы (объекта) в качестве переменных ее состояния (такими координатами, например, могут быть выходной сигнал y(t) и n-1 его производных) xi(t), i=1,2,...,n, данную систему можно описать уравнениями для переменных состояния где X(t) = [ x1(t), x1(t),..., xn(t) ]T - вектор-столбец переменных состояния; A,B,C и D при скалярных u(t) и y(t) – соответственно матрица размера n x n, векторы размера n x 1 x 1 и скаляр (при векторных u(t) и y(t) – матрицы соответствующих размеров). Приведенные модели являются эквивалентными, то есть, зная любую из них, можно получить все остальные. 3. Разностные уравнения. Для объектов, функционирование которых представляется для дискретного времени tk=kT (в данном случае T – интервал дискретизации), то есть для дискретных объектов, наиболее общим видом описания является разностное уравнение (аналог дифференциального) yk + a1yk-1 +... + amyk-na = b1uk + b2uk-1 + b3uk-2 +... + bnbuk-nb+1 где yk-i = y [ (k – i)T ], uk-j = u [ (k – j)T ]. 4. Z-преобразование. Связь между сигналами может быть отражена также через дискретную свертку где g i – ординаты весовой решетчатой функции объекта, или, с использованием аппарата Z-преобразования где z = e pT, через дискретную передаточную функцию |
 . (7.1)
. (7.1)


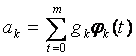 .
.
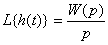 ;
;
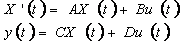 ,
,




