
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибір оптимальної потужності джерел розосередженої генерації при мінімумі поточних витратСодержание книги
Поиск на нашем сайте
Поставлена задача розглянута і вирішена для двох видів схем з різними даними Схема 1. Для схеми, наведеної нижче (рис.4.6), для покупки установки розосередженої генерації береться кредит в банку строком на 5 років під 12% річних. Обрати оптимальну потужність установки генерації при мінімумі поточних витрат на втрати потужності і виплату кредиту банку. Згідно договору повернення кредиту раніше неможливе, а також відсотки нараховуються як складні. Прийняти ціну генерації 1 кВт на стороні НН ТП К0, рівною 1500 грн./кВт., ціна 1 кВт максимальної потужності втрат прийняти С0=1000 грн./кВт.рік. Втрати враховувати у лініях, трансформаторах.
Рисунок 4.6 Розрахункова схема
Обчислимо спочатку, скільки кожного року потрібно виплачувати банку коштів за 1 кВт. Враховуючи складний відсоток, формула для розрахунку нарощеної суми в кінці n-го року за умови, що проценти нараховуються один раз на рік, має вигляд:
де S – повна сума за n років; P – розмір кредиту; j – процентна ставка; n – строк кредиту. Тоді, кожен рік виплачується за кожен 1 кВт:
або коефіцієнт відрахувань за кредит дорівнює Загальний вид цільової функції:
F(Pгi) = В = ЕК + ΔРС0,
де Е – коефіцієнт відрахувань за кредит. Підставляючи значення та розкриваючи дужки, отримаємо цільову функцію:
Класичний метод (без врахування обмежень по режиму напруги)
Визначимо часткові похідні та прирівняємо їх до нуля
Отримали систему рівнянь з двома невідомими, вирішуючи яку отримаємо оптимальні потужності джерел розосередженої генерації:
Pг1 = 84,7545 кВт, Pг2 = 111,1737 кВт.
Ці значення забезпечують екстремум функції. Визначивши знак других похідних, впевнюємося, що витрачена кількість коштів оптимальна у даній точці (мінімальні).
Метод множників Лагранжа (з врахуванням обмежень по режиму напруги)
Для нашої задачі введемо обмеження по режиму напруги. Обмеження у вигляді рівності запишеться таким чином
де
тобто після генерації відхилення напруги у віддаленій точці мережі 0,38 кВ першої ТП повинно бути рівним -5%. Для даних умов запишемо функцію Лагранжа
У результаті диференціювання по Pг1, Pг2, λ та прирівнювання похідних до нуля отримаємо систему з трьох рівнянь з трьома невідомими.
Розв’язавши отриману систему рівнянь, знаходимо значення величин Pг1, Pг2, що обертають у мінімум цільову функцію з врахуванням обмежень.
Pг1 = 247,1745 кВт; Pг2 = 46,1932 кВт.
Схема 2. В існуючій схемі електропостачання (рисунок 4.7) потрібно визначити потужності джерел розосередженої генерації Вихідні дані: напруга мережі U=10 кВ; опори ліній активні навантаження вузлів 1 та 2 питомі витрати на установку джерел розосередженої генерації питомі витрати на покриття втрат активної потужності
Рисунок 4.7 Схема електропостачання
Цільова функція, що представляє сумарні втрати на установку джерел розосередженої генерації та покриття втрат активної потужності в схемі, має вигляд:
де
Числовий коефіцієнт Для розв’язання задачі виберемо метод по координатного «спуску». Розраховуємо часткові похідні цільової функції
Приймаємо початкове наближення:
Очевидно, що в напрямку змінної У напрямку змінної Приймаємо величину кроку
Другий крок: Третій крок: Очевидно, що «спуск» по змінній Виконаємо новий третій крок Точка з координатами
Висновки
1. В роботі розглянуті питання застосування методів нелінійного програмування для визначення місць та оптимальних значень установок розосередженої генерації.
2. Запропоновано використовувати математичні моделі і методи оптимального вибору потужностей засобів генерації по типу "компенсації активної потужності" по аналогії з відпрацьованими методами вирішенням задач компенсації реактивної потужності. 3. Наведені приклади вирішення задач вибору засобів розосередженої генерації з урахуванням економічних і технічних вимог і обмежень.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.209 (0.011 с.) |


 ,
, грн.,
грн.,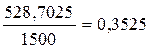 .
.

 ,
, ,
,
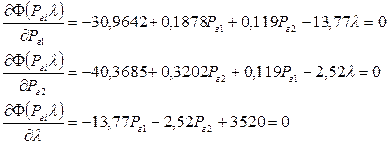
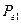 та
та 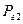 в вузлах 1 та 2 виходячи з умови мінімуму сумарних затрат на установку цих джерел та покриття втрат активної потужності в схемі.
в вузлах 1 та 2 виходячи з умови мінімуму сумарних затрат на установку цих джерел та покриття втрат активної потужності в схемі. ,
,  ;
; ,
,  ;
; ;
; .
.
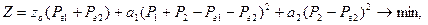
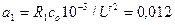 ;
; ;
; вводимо для приведення всіх складових цільової функції до однієї розмірності (у.о.).
вводимо для приведення всіх складових цільової функції до однієї розмірності (у.о.). по змінним
по змінним  ;
; .
. ,
, 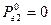 . Для цих значень обчислимо значення цільової функції та її часткові похідні:
. Для цих значень обчислимо значення цільової функції та її часткові похідні: ;
; ;
;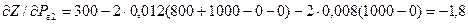 .
.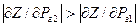 .
.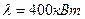 . Перше наближення (перший крок) буде
. Перше наближення (перший крок) буде  ,
,  . Значення цільової функції
. Значення цільової функції
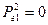 ,
,  . Значення цільової функції
. Значення цільової функції 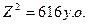 .
.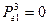 ,
,  . Значення цільової функції
. Значення цільової функції 
 , та повернутися до значень змінних
, та повернутися до значень змінних  ,
,  . Значення цільової функції
. Значення цільової функції  . Рух в напрямку змінної
. Рух в напрямку змінної 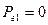 ,
,  знаходиться в межах мінімуму цільової функції
знаходиться в межах мінімуму цільової функції 


