
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачі для методів нелінійного програмування
Основна ідея математичного моделювання задач урахування джерел розосередженої генерації заключається в наступному. Розглянемо просту схему електропостачання (рисунок 4.1), що включає в себе лінію з активним опором
Рисунок 4.1 Проста схема генерації активної потужності
Втрати активної потужності в лінії при відсутності у споживача джерела розосередженої генерації (
При установці у споживача джерела генерації (
Таким чином, генерація активної потужності джерелами розосередженої генерації дозволяє зменшити втрати потужності в схемі електропостачання та, відповідно, покращити техніко-економічні показники цієї схеми. З рівнянь (4.1) та (4.2) видно, що втрати потужності При проектуванні схеми електропостачання, як правило, мінімізується грошові затрати на цю схему. Зниження втрат потужності за рахунок встановлення джерел розосередженої генерації зменшує затрати на схему. Однак установки розосередженої генерації потребують грошових затрат. У зв’язку з цим постає задача визначення оптимальної потужності установок розосередженої генерації, що будуть відповідати мінімуму сумарних затрат. Така задача може бути вирішена методами нелінійного програмування. Будь-яка задача є нелінійною, коли цільова функція або обмеження нелінійні. До нелінійних енергетичних задач відносять вибір оптимальної потужності джерел розосередженої генерації при мінімізації поточних витрат на втрати потужності та виплату кредиту, як без обмежень, так і з обмеженнями по напрузі, вибір оптимальної потужності установок генерації при мінімізації втрат потужності в мережі, визначення оптимального місця встановлення джерел розосередженої генерації, тощо. До нелінійних задач також відносять задачі цілочислового програмування, хоча цільова функція та обмеження в цих задачах лінійні. Їх неможливо розв’язати методами лінійного програмування внаслідок вимоги того, що розв’язок повинен бути цілочисловий. Прикладом застосування таких задач в енергетиці може бути знаходження кількості трансформаторів визначеної потужності при мінімумі капітальних витрат, тощо.
Класичний метод Якщо задача вирішується без врахування обмежень, а цільову функцію можна диференціювати, то можна застосовувати метод прямого диференціювання. В точці екстремуму цільової функції F(x1, x2,... xn) перші похідні дорівнюють нулю
Рішення системи з n рівнянь з n невідомими і є рішенням задачі. Метод не дає однозначного рішення – при отриманні результату невідомо, що визначено – мінімум або максимум. Необхідно проводити додаткові дослідження, що заключаються в отриманні та аналізі похідних другого порядку
Вирішення задачі оптимізації класичним методом має суттєвий недолік – метод не враховує обмежень. Виконав розрахунок з врахуванням обмежень в даному випадку можна, застосовуючи метод невизначених множників Лагранжа.
Метод множників Лагранжа Задача складається у відшуканні вектора змінних управління х, що забезпечує досягнення екстремуму цільової функції F(x) та задовольняє обмеженням:
g2(x1, x2, …, xn) = 0 (4.5) ……………………. gn(x1, x2, …, xn) = 0,
причому обмеження представляються у вигляді рівностей. Для рішення задачі потрібно сформулювати функцію Лагранжа:
де λi – невизначені множники Лагранжа і = 1,2,...,m. Для знаходження екстремуму необхідно визначити перші похідні функції Лагранжа по x та λ і прирівняти їх до нуля:
Отримуємо n+m рівнянь з n+m невідомими. Рішення системи рівнянь дозволяє знайти цікавлячий нас вектор.
|
||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.174.76 (0.008 с.) |
 , яка зв’язує джерело живлення напругою
, яка зв’язує джерело живлення напругою  та споживача потужністю
та споживача потужністю  .
.
 ) складають
) складають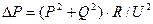 , (4.1)
, (4.1) ) ці втрати зменшуються до величини
) ці втрати зменшуються до величини . (4.2)
. (4.2)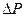 мають дві складові: втрати від протікання по лінії активної потужності
мають дві складові: втрати від протікання по лінії активної потужності  або
або  і втрати від протікання по лінії реактивної потужності
і втрати від протікання по лінії реактивної потужності  . Оскільки генерація активної потужності впливає тільки на першу складову втрат, то далі будемо розглядати втрати від протікання по лінії тільки активних потужностей.
. Оскільки генерація активної потужності впливає тільки на першу складову втрат, то далі будемо розглядати втрати від протікання по лінії тільки активних потужностей. (4.3)
(4.3) (4.4)
(4.4) g1(x1, x2, …, xn) = 0,
g1(x1, x2, …, xn) = 0, , (4.6)
, (4.6) (4.7)
(4.7)


