
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
L. 3.11. Виртуальная и действительная работа напряжений
Как отмечалось, решение краевой задачи в общем случае (когда задача статически неопределима) требует совместного решения трех систем уравнений: статики, геометрии и физики. Имеется еще одна – четвертая сторона механики, весьма полезная для решения задач. Это – «энергетическая» сторона, оперирующая величинами измеренными в джоулях (отметим, что в тех же величинах измеряются и просто моменты сил). Она получена в результате совместного использования статической и геометрической сторон, не имеет ни малейшего отношения к свойствам материалов (в частности, к закону сохранения) и заменяет, когда это полезно, геометрическую либо статическую сторону. В теории напряжений, в отличие от теории деформаций, не приходится сопоставлять два состояния: начальное, недеформированное и текущее, актуальное, деформированное. Рассматривается только последнее. Статическая сторона механики представляет самостоятельную сторону, и факт, что рассматриваемые напряжения действуют в деформированном теле, не играет ни какой роли. Следует лишь не забывать, что напряжения на площадке Принцип виртуальных работ (перемещений) формулируется по-разному, хотя означает одно и то же. Чтобы не мучиться со знаками, сформулируем его так: если выполняются условия равновесия и совместности деформаций, то при любом возможном (виртуальном) смещении материальных частиц тела работа внешних сил, приложенных к телу, равна работе внутренних (напряжений). Виртуальными называются бесконечно малые смещения, удовлетворяющие условиям совместности деформаций. При бесконечно малых смещениях
а общая работа
и, поскольку тензор напряжений
где Тензор Для подсчета действительной работы необходимо интегрировать работу по пути: для истории напряжения в данном элементарном материальном объеме s(t) (тензор напряжения Коши) необходимо еще знать историю деформаций e*(t). Таким образом, можно вывести ряд полезных формул.
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.160.219 (0.005 с.) |
 (нормаль к площадке
(нормаль к площадке  , величина площади ds,
, величина площади ds,  ) представляет интенсивность распределенной силы, подсчитываемую для деформированной площадки. До деформирования эта площадка имела и другую нормаль, и другую площадь. В остальном все соображения статики (или динамики) остаются в силе, напряжения в различных площадках (деформированного тела) представляют линейную функцию нормали
) представляет интенсивность распределенной силы, подсчитываемую для деформированной площадки. До деформирования эта площадка имела и другую нормаль, и другую площадь. В остальном все соображения статики (или динамики) остаются в силе, напряжения в различных площадках (деформированного тела) представляют линейную функцию нормали  ); тензор s называют тензором Коши в отличие от некоторых искусственных модификаций тензора напряжений (например, тензора Пиолы–Кирхгофа, смысл которого весьма туманен).
); тензор s называют тензором Коши в отличие от некоторых искусственных модификаций тензора напряжений (например, тензора Пиолы–Кирхгофа, смысл которого весьма туманен).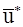 точек среды, на которые действуют силы, работа последних может вычисляться в предположении их постоянства (скалярное произведение вектора силы на вектор смещения
точек среды, на которые действуют силы, работа последних может вычисляться в предположении их постоянства (скалярное произведение вектора силы на вектор смещения  ). То же можно сказать и о работе внутренних сил (напряжений), но с оговоркой: работа последних на смещениях
). То же можно сказать и о работе внутренних сил (напряжений), но с оговоркой: работа последних на смещениях  При записи условий равновесия и некоторых уравнений энергетического характера возникает необходимость вычисления виртуальной работы внутренних сил. Например, в принципе возможных (виртуальных) перемещений (работ, мощностей) необходимо научиться вычислять работу напряжений на возможных перемещениях (дисторсиях). Следует помнить, что виртуальные деформации и перемещения – не только разрешены связями, но и бесконечно малы. Поэтому выражение для удельной работы внутренних сил (в единице объема, который является бесконечно малым) остается тем же, что и в теории упругости, когда используется линеаризирующая задачу гипотеза бесконечной малости всех смещений. Для наглядности удобно рассмотреть элементарный параллелепипед с гранями, нормали к которым представляют декартов базис
При записи условий равновесия и некоторых уравнений энергетического характера возникает необходимость вычисления виртуальной работы внутренних сил. Например, в принципе возможных (виртуальных) перемещений (работ, мощностей) необходимо научиться вычислять работу напряжений на возможных перемещениях (дисторсиях). Следует помнить, что виртуальные деформации и перемещения – не только разрешены связями, но и бесконечно малы. Поэтому выражение для удельной работы внутренних сил (в единице объема, который является бесконечно малым) остается тем же, что и в теории упругости, когда используется линеаризирующая задачу гипотеза бесконечной малости всех смещений. Для наглядности удобно рассмотреть элементарный параллелепипед с гранями, нормали к которым представляют декартов базис  , со стороны dri. Сила
, со стороны dri. Сила  (или на противоположной площадке –
(или на противоположной площадке –  ,
,  – виртуальное бесконечно малое изменение волокна
– виртуальное бесконечно малое изменение волокна  (которое когда-то было
(которое когда-то было  , где
, где  – дисторсия), если предположить, что площадка
– дисторсия), если предположить, что площадка  (“задняя” площадка) неподвижна. Значит, виртуальная работа напряжения на этой площадке есть
(“задняя” площадка) неподвижна. Значит, виртуальная работа напряжения на этой площадке есть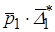 , (3.35)
, (3.35) . Учитывая, что
. Учитывая, что  ,
,  , заметим:
, заметим:
 симметричен (закон парности касательных напряжений)
симметричен (закон парности касательных напряжений) ,
, .
. представляет тензор бесконечно малых виртуальных деформаций деформированного состояния. Естественно, тензор напряжений
представляет тензор бесконечно малых виртуальных деформаций деформированного состояния. Естественно, тензор напряжений  ,
,  ,
, 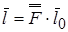

 .
.


