
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
E. 3.5. Лабораторная система отсчета s и eСтр 1 из 5Следующая ⇒
A. 3.1. Тензор напряжений Итак, дано тело произвольных размеров и формы; известно, что оно неподвижно но и нагружено внешними силами так, что во всех его элементарных объемах на одинаковых площадках действуют одинаковые силы. Такое напряженное состояние тела называют однородным. Для рассмотрения напряжений в нем можно выбрать любую его часть любой формы и размера. Исследуется статическая сторона явления: удобно считать тело твердым, хотя анализ справедлив для любой Среды. Ключом к рассмотрению является известный метод сечений. Напомним, что напряжением Чтобы выделить полностью часть тела, минимально требуется провести четыре сечения, получив тем самым четырехгранник с наружными нормалями Неподвижность тела при действии этих сил требует, чтобы суммарная сила была равна нулю
Таким образом, достаточно знать три напряжения на каких-либо трех площадках
Как видим, вектор Варьируя положение четвертой площадки, найдем напряжения на всех площадках. Следовательно, напряженное состояние однозначно определяется векторами Удобнее всего для этой цели использовать три ортогональные площадки, обозначим их нормали
(например, из упомянутого выше условия
Объект При получении тензора s мы использовали лишь одно условие равновесия (по силам); в действительности их два. Второе условие – по моментам – запишем для куба со стороной а. Пара сил на площадках
то есть тензор s симметричен. В сопротивлении материалов это условие называют законом парности касательных напряжений (s12=s21, s13=s31, s23=s32). Простейшее напряженное состояние – одноосное, когда тензор s сводится к диаде
ранг его равен единице. Нетрудно видеть, что ранг матриц
равен единице, значит, все они представляют координаты тензора (3.3) в различных декартовых базисах. Векторы Плоскому напряженному состоянию отвечают тензоры второго ранга; они приводятся к виду
li – главные напряжения (вместе с l=0),
В механике жидкостей наиболее популярно шаровое напряженное состояние
B. 3.2. Тензор дисторсии При рассмотрении геометрической стороны той же ситуации (однородное деформированное состояние некоторого тела) первая трудность связана с необходимостью включить в поле зрения, кроме текущего, начальное, недеформированное состояние. Нам придется ввести в рассмотрение понятие материального волокна (это совокупность материальных точек среды, лежащих на некоторой линии). Нам достаточно будет иметь дело с прямыми волокнами; их удобно отображать векторами, характеризующими длину и направления волокна. Если начальное положение волокна отражается вектором
Однородность деформированного состояния означает, что если в начальном состоянии тело представить совокупностью одинаковых параллелепипедов (кирпичиков), то в деформированном состоянии все кирпичики деформированы одинаково, грани кирпичиков остаются плоскими. Следовательно, все материальные плоскости (совокупность материальных точек или волокон, лежащих в одной плоскости) в процессе деформирования остаются плоскими; равноотстоящие множества параллельных плоскостей остаются равноотстоящими множествами плоскостей. Таким образом, все бесконечное множество начальных волокон, которым отвечает некоторый один вектор
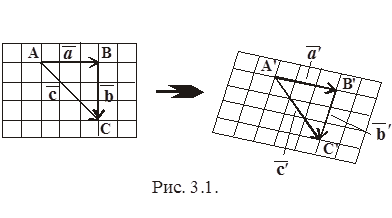
она характеризует данное однородное деформированное состояние тела. На рис. 3.1 показано одно из свойств этой функции. Треугольник АВС переходит в новое положение
функция суммы равна сумме функций. Нетрудно заметить и другое свойство
 . .
Следовательно, функция
Заметим, что и при неоднородном деформированном состоянии волокна В твердых телах деформации обычно довольно малы, волокна
Как следует из выражения (6), изменение волокна
Тензор D зависимости
C. 3.3. Изометрическое преобразование Другая сложность при изучении характеристик деформированного состояния связана с тем, что деформации могут отсутствовать при ненулевом аффиноре (и ненулевой дисторсии): тело может просто повернуться на некоторый угол j вокруг некоторой оси
Особенность жесткого поворота в том, что для любых двух волокон справедливо равенство
такое преобразование называют еще изотермическим (длины и углы остаются прежними!). Отсюда
т.е.
– это свойство ортогональных тензоров, обращающихся транспонированием (при обращении поворот на угол j преобразуется в поворот вокруг той же оси
При малом повороте, когда
D. 3.4. Тензор деформации Рассмотрим другой частный случай: тензор А симметричен, симметричен и тензор дисторсии. Будем их обозначать в этом случае
тензор e назовем тензором деформации (в механике рассматривают и другие тензоры, называемые также тензорами деформации). Как и любой симметричный тензор, тензор e имеет три главных направления
эти направления совпадают с главными направлениями аффинора
В случае одноосной деформации
На рис. 3.2 штриховой линией показана совокупность начальных положений единичных волокон; эллипс – положения концов этих волокон после деформирования; начала волокон считаются неподвижными. Смещение концов всех волокон, как видно из выражения (13), параллельны оси В случае плоской деформации
если главные деформации имеют одинаковые знаки, недеформированными остаются лишь волокна, ортогональные плоскости В отличии от тензора деформации, ранг аффинора
I. 3.10.1. Изотропное тело Тензор Довольно просто убедиться, что нет ничего изотропного кроме единичного тензора Из этого материала можно получить три тензора
причем первый из них - нужной симметрии, а два другие несимметричны. В этом легко убедиться, умножая на произвольный тензор
Поскольку тензор
Зато симметричен тензор
который выделяет из тензора симметричную часть
Для симметричных тензоров Итого - всего-то 2 тензора!
Подставив в 3Г, получим
На первую часть С уравнением (3.33) еще можно работать, но дальше будет труднее (для анизотропных сред). Поэтому попробуем чуть упростить. Вместо тензоров
который, как можно показать (а мы в этом просто убедимся) удовлетворяет условию
Исходя из требования (3.34), быстро находим
И убеждаемся:
Закон Гука сейчас принимает более простой, на наш взгляд, вид:
Этот вид хорош тем, что легко обращается (попробуйте получить тензор
позволяет легко вычислять работу
и вообще удобен. А что в Нетрудно установить:
Из закона Гука следует, что в пространстве
A. 3.1. Тензор напряжений Итак, дано тело произвольных размеров и формы; известно, что оно неподвижно но и нагружено внешними силами так, что во всех его элементарных объемах на одинаковых площадках действуют одинаковые силы. Такое напряженное состояние тела называют однородным. Для рассмотрения напряжений в нем можно выбрать любую его часть любой формы и размера. Исследуется статическая сторона явления: удобно считать тело твердым, хотя анализ справедлив для любой Среды. Ключом к рассмотрению является известный метод сечений. Напомним, что напряжением Чтобы выделить полностью часть тела, минимально требуется провести четыре сечения, получив тем самым четырехгранник с наружными нормалями Неподвижность тела при действии этих сил требует, чтобы суммарная сила была равна нулю
Таким образом, достаточно знать три напряжения на каких-либо трех площадках
Как видим, вектор
Варьируя положение четвертой площадки, найдем напряжения на всех площадках. Следовательно, напряженное состояние однозначно определяется векторами Удобнее всего для этой цели использовать три ортогональные площадки, обозначим их нормали
(например, из упомянутого выше условия
Объект При получении тензора s мы использовали лишь одно условие равновесия (по силам); в действительности их два. Второе условие – по моментам – запишем для куба со стороной а. Пара сил на площадках
то есть тензор s симметричен. В сопротивлении материалов это условие называют законом парности касательных напряжений (s12=s21, s13=s31, s23=s32). Простейшее напряженное состояние – одноосное, когда тензор s сводится к диаде
ранг его равен единице. Нетрудно видеть, что ранг матриц
равен единице, значит, все они представляют координаты тензора (3.3) в различных декартовых базисах. Векторы Плоскому напряженному состоянию отвечают тензоры второго ранга; они приводятся к виду
li – главные напряжения (вместе с l=0),
В механике жидкостей наиболее популярно шаровое напряженное состояние
B. 3.2. Тензор дисторсии При рассмотрении геометрической стороны той же ситуации (однородное деформированное состояние некоторого тела) первая трудность связана с необходимостью включить в поле зрения, кроме текущего, начальное, недеформированное состояние. Нам придется ввести в рассмотрение понятие материального волокна (это совокупность материальных точек среды, лежащих на некоторой линии). Нам достаточно будет иметь дело с прямыми волокнами; их удобно отображать векторами, характеризующими длину и направления волокна. Если начальное положение волокна отражается вектором Однородность деформированного состояния означает, что если в начальном состоянии тело представить совокупностью одинаковых параллелепипедов (кирпичиков), то в деформированном состоянии все кирпичики деформированы одинаково, грани кирпичиков остаются плоскими. Следовательно, все материальные плоскости (совокупность материальных точек или волокон, лежащих в одной плоскости) в процессе деформирования остаются плоскими; равноотстоящие множества параллельных плоскостей остаются равноотстоящими множествами плоскостей. Таким образом, все бесконечное множество начальных волокон, которым отвечает некоторый один вектор
она характеризует данное однородное деформированное состояние тела. На рис. 3.1 показано одно из свойств этой функции. Треугольник АВС переходит в новое положение
функция суммы равна сумме функций. Нетрудно заметить и другое свойство
 . .
Следовательно, функция
Заметим, что и при неоднородном деформированном состоянии волокна В твердых телах деформации обычно довольно малы, волокна
Как следует из выражения (6), изменение волокна
Тензор D зависимости
C. 3.3. Изометрическое преобразование Другая сложность при изучении характеристик деформированного состояния связана с тем, что деформации могут отсутствовать при ненулевом аффиноре (и ненулевой дисторсии): тело может просто повернуться на некоторый угол j вокруг некоторой оси
Особенность жесткого поворота в том, что для любых двух волокон справедливо равенство
такое преобразование называют еще изотермическим (длины и углы остаются прежними!). Отсюда
т.е.
– это свойство ортогональных тензоров, обращающихся транспонированием (при обращении поворот на угол j преобразуется в поворот вокруг той же оси При малом повороте, когда
D. 3.4. Тензор деформации Рассмотрим другой частный случай: тензор А симметричен, симметричен и тензор дисторсии. Будем их обозначать в этом случае
тензор e назовем тензором деформации (в механике рассматривают и другие тензоры, называемые также тензорами деформации). Как и любой симметричный тензор, тензор e имеет три главных направления
эти направления совпадают с главными направлениями аффинора
В случае одноосной деформации
На рис. 3.2 штриховой линией показана совокупность начальных положений единичных волокон; эллипс – положения концов этих волокон после деформирования; начала волокон считаются неподвижными. Смещение концов всех волокон, как видно из выражения (13), параллельны оси В случае плоской деформации
если главные деформации имеют одинаковые знаки, недеформированными остаются лишь волокна, ортогональные плоскости В отличии от тензора деформации, ранг аффинора
E. 3.5. Лабораторная система отсчета s и e В общем случае аффинор А не симметричен и не ортогонален. Сфера преобразуется в эллипсоид, но главные оси эллипсоида не являются главными направлениями аффинора. Происходит и деформирование тела, и его поворот. О “физической” стороне дела будет сказано ниже, но сейчас полезно отметить, что деформацию инициирует тензор напряжений, тогда как поворот не требует усилий; он связан лишь с условиями закрепления тела. Поэтому при записи “физических ” соотношений используют термины “напряжения” и “деформации”, оставляя в стороне поворот. Отсюда следует необходимость решения задачи: как, зная тензор А, определить тензор e. Любое преобразование можно рассматривать как совокупность нескольких преобразований. Например, если Итак, имея тензор А, можно представить два варианта развития событий:
(деформация, затем поворот) или, наоборот,
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.190.144 (0.144 с.) |
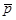 называют интенсивность силы, передающейся через некоторую площадку (с единичной нормалью
называют интенсивность силы, передающейся через некоторую площадку (с единичной нормалью  ) от одной части тела к другой, отделенной мысленно этой площадкой. Однородность означает, что вектор
) от одной части тела к другой, отделенной мысленно этой площадкой. Однородность означает, что вектор  . Силы, действующие по этим граням, находятся умножением напряжений
. Силы, действующие по этим граням, находятся умножением напряжений  (постоянных на каждой грани) по площади граней
(постоянных на каждой грани) по площади граней  . Из геометрических соображений следует, что эти площади связаны между собой и достаточно знать
. Из геометрических соображений следует, что эти площади связаны между собой и достаточно знать  , чтобы, по нормалям
, чтобы, по нормалям 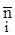 найти все
найти все  равна нулю).
равна нулю). (i=1…4).
(i=1…4).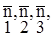 чтобы найти четвертое:
чтобы найти четвертое:
 (3.1)
(3.1) представляет линейную форму трех векторов
представляет линейную форму трех векторов  , коэффициенты которой зависят только от векторов
, коэффициенты которой зависят только от векторов  .
. (они послужат ортами декартова базиса), четвертую – просто
(они послужат ортами декартова базиса), четвертую – просто 
 ), и выражение (3.1) примет вид
), и выражение (3.1) примет вид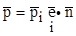 , i=1…3 (3.2)
, i=1…3 (3.2) , представляющий, как мы знаем, двухвалентный тензор, обозначают s и называют тензором напряжений. Выражение (3.2) показывает смысл этого тензора: его проекция на нормаль к любой площадке определяет напряжение на этой площадке. В частности, это относится и к площадкам
, представляющий, как мы знаем, двухвалентный тензор, обозначают s и называют тензором напряжений. Выражение (3.2) показывает смысл этого тензора: его проекция на нормаль к любой площадке определяет напряжение на этой площадке. В частности, это относится и к площадкам 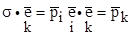 ). Таким образом, напряжение
). Таким образом, напряжение  на площадке
на площадке  и, таким образом,
и, таким образом,  – касательное напряжение на второй, а не на первой площадке.
– касательное напряжение на второй, а не на первой площадке. и
и  создают момент
создают момент  , аналогично найдутся еще два; сумма моментов
, аналогично найдутся еще два; сумма моментов  должна быть равна нулю. Отсюда
должна быть равна нулю. Отсюда ,
, , (3.3)
, (3.3) ,
, 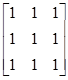 ,
, 

 (3.4)
(3.4) – главные направления тензора.
– главные направления тензора. , величину l, обычно положительную, обозначают p и называют давлением. Из простейших состояний можно еще упомянуть чистый сдвиг (
, величину l, обычно положительную, обозначают p и называют давлением. Из простейших состояний можно еще упомянуть чистый сдвиг ( ,
,  , плоское напряженное состояние) и цилиндрическое (
, плоское напряженное состояние) и цилиндрическое ( ).
). , то конечное будем обозначать
, то конечное будем обозначать  .
. , переходящим в
, переходящим в  . Иначе говоря, существует функция
. Иначе говоря, существует функция ; (3.5)
; (3.5) ; его стороны
; его стороны  – в
– в 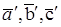 ; нетрудно заметить, что
; нетрудно заметить, что  ,
,  и, таким образом,
и, таким образом, ,
, :
:
 . (3.6)
. (3.6) переходят в положения
переходят в положения  , но второе условие линейности функции
, но второе условие линейности функции  сопоставимы и более информативна разница между этими волокнами
сопоставимы и более информативна разница между этими волокнами . (3.7)
. (3.7)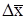 представляет также линейную функцию его начального положения
представляет также линейную функцию его начального положения (3.8)
(3.8) (3.9)
(3.9) называют тензором дисторсии.
называют тензором дисторсии. . В п.2 мы рассматривали такое преобразование
. В п.2 мы рассматривали такое преобразование  ; аффинор при этом имел вид
; аффинор при этом имел вид
 ;
;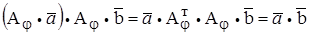 ,
,
 ,
, 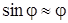 , тензор
, тензор  оказывается равным
оказывается равным  , тензор дисторсии
, тензор дисторсии  – кососимметричен.
– кососимметричен. и
и , (3.10)
, (3.10) , (3.11)
, (3.11) . (3.12)
. (3.12) преобразование (3.8) принимает вид
преобразование (3.8) принимает вид . (3.13)
. (3.13) . Волокна ортогональные
. Волокна ортогональные  не деформируются и не поворачиваются; волокна, параллельные
не деформируются и не поворачиваются; волокна, параллельные  ) равно
) равно  .
.  Остальные волокна и удлиняются, и поворачиваются. Стержень с осью
Остальные волокна и удлиняются, и поворачиваются. Стержень с осью  , поперечные сечения остаются плоскими, поперечными, недеформированными.
, поперечные сечения остаются плоскими, поперечными, недеформированными. ,
, . Круг в этой плоскости также превращается в эллипс с главными осями
. Круг в этой плоскости также превращается в эллипс с главными осями  . Если
. Если  , то круг остается кругом и волокна в плоскости
, то круг остается кругом и волокна в плоскости  положительны. Определитель
положительны. Определитель  представляет отношение нового объема тела к начальному и равен
представляет отношение нового объема тела к начальному и равен  .
.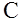 - набор квадриад - должен быть таким, чтобы ни одно из направлений не было выделено или, наоборот, отделено. Иначе говоря, при построении тензора можно использовать только изотропный строительный материал.
- набор квадриад - должен быть таким, чтобы ни одно из направлений не было выделено или, наоборот, отделено. Иначе говоря, при построении тензора можно использовать только изотропный строительный материал. (или шарового
(или шарового  ). На первый взгляд, здесь выделены три направления
). На первый взгляд, здесь выделены три направления  , но мы знаем, что в другом декартовом базисе тензор имеет те же координаты (
, но мы знаем, что в другом декартовом базисе тензор имеет те же координаты ( ). Тензор
). Тензор  - тоже изотропный - не обладает симметрией.
- тоже изотропный - не обладает симметрией.

 произволен, ответ не симметричен, что не отвечает требованию (3.30).
произволен, ответ не симметричен, что не отвечает требованию (3.30).

 - тензор тождественного преобразования.
- тензор тождественного преобразования.
 . (3.33)
. (3.33) деформация влияет не так, как на девиатор! Две разные константы.
деформация влияет не так, как на девиатор! Две разные константы. ,
,  (3.34)
(3.34) .
.


 ):
):

 ?
?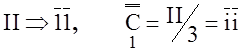 – проецирующий тензор,
– проецирующий тензор, ,
, – тоже проецирующий,
– тоже проецирующий,
 нет изотропных направлений (
нет изотропных направлений ( – независимо от направления
– независимо от направления  ).
).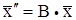 ,
, 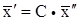 , то
, то  ; аффинор представляет произведение двух аффиноров. Разбиение на два не означает, что сначала произошло деформирование В, затем С; просто это могло произойти в такой последовательности. Если одно из движений (В или С) представляло жесткий поворот, то с точки зрения физических особенностей процесса не важно, был ли поворот после деформирования или в процессе деформирования: поворот на процесс не влияет. Возможно разложение и на большее число движений, но практический смысл имеет только такое разложение: деформация без поворота и поворот без деформации.
; аффинор представляет произведение двух аффиноров. Разбиение на два не означает, что сначала произошло деформирование В, затем С; просто это могло произойти в такой последовательности. Если одно из движений (В или С) представляло жесткий поворот, то с точки зрения физических особенностей процесса не важно, был ли поворот после деформирования или в процессе деформирования: поворот на процесс не влияет. Возможно разложение и на большее число движений, но практический смысл имеет только такое разложение: деформация без поворота и поворот без деформации. (3.14)
(3.14) (3.15)
(3.15)


