
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
G. 3.7. Подходы Лагранжа и Эйлера. Другие тензоры деформаций
Не всегда удобно пользоваться функцией
Использование в качестве независимого переменного характеристик текущего (деформированного) состояния отличает подход Эйлера; он особенно удобен при анализе течения жидкостей. Первый подход, более широко используемый в механике твердых тел, связывают с именем Лагранжа. Как отмечалось, изометрическое деформирование, при котором все длины и углы неизменны, то есть деформирование отсутствует, характеризуется неизменностью скалярного произведения двух произвольных волокон:
или
Тензоры А и В в этом случае ортогональны, Если деформация происходит, то тензоры
первый называют тензором деформаций Грина-Лагранжа, второй – тензором деформаций Коши. Они обычно ассоциируются с выражениями для квадрата длины волокна:
Если деформации малы, то не очень информативно сравнение квадратов длин в начальном и конечном состоянии волокна; удобнее анализировать их разность. Поэтому вводят тензоры
– лагранжев тензор бесконечно малых деформаций (это термин: смысл его не обсуждается) и
– тензор деформаций Альманси-Эйлера. Эти тензоры используются в уравнениях
Любой из введенных тензоров G, C, 3.8. Тензор малых деформаций. Теорию деформаций можно рассматривать как обобщение известного опре-деления e=Dl/l0 , в котором Dlºl – l0 , где l0, l – длина некоторого материального волокна в начальном (недеформированном) и в текущем (деформированном) состояниях, e – линейная деформация этого волокна. Запишем это выражение по-другому: Dl º l – l0=e × l0. (3.27) Если рассматривать l0 как аргумент, а Dl – как функцию, то в выражении (3.27) можно увидеть линейную зависимость Dl(l0) для произвольно выбираемых длин l0. Оператором этой зависимости является деформация.
D l º l – l 0=D l (l 0) (3.28) (l – вектор, характеризующий текущие длину и направление того же волокна). Этот вектор определяет не только изменение длины, но и поворот волокна, который в начальном состоянии характеризовался вектором l 0 (рис.3.4). На рисунке показаны две материальные точки – в недеформированном (A,B) и в деформированном (A¢,B¢) состояниях. Ниже показано “изменение” волокна (рис. 3.4). На рисунке величина D l утрирована; в действительности деформация и поворот обычно весьма малы. Гипотетически их считают бесконечно малыми, тогда проекция D l на направление l 0 (скалярное произведение D l× n, где n – единичный вектор вдоль l 0) определяет деформацию волокна, а проекция на вектор t, ортогональный n – угол поворота j: D l n =e l0, D l × t =j l0. (3.29) Исходя из обычных соображений дифференцируемости полей смещений доказывают, что для бесконечно коротких волокон l 0 функция (3.27) линейна. Это означает, что если взять вдвое более длинное волокно, то и его изменение будет вдвое большим. Поэтому достаточно рассмотреть волокна определенной длины – например, единичной. В частности, изменение D n единичноговолокна n (рис.9.8) при проецировании на оси n и t сразу определяет те же, что и в (3.28) деформацию и поворот: (D n)× n =e, (D n)× t =j. (3.28')
Введем декартовы координаты x, y и будем отображать векторы матрица- ми-столбцами координат (например, n ® [ nx, ny ] T ). Тогда функция (3.27), как и всякая линейная вектор-функция вектора, отобразится матрицей
Матрицу D называют матрицей дисторсии. Полученное выражение, с одной и той же матрицей дисторсии, справедливо для любых (бесконечно коротких) векторов l 0 в окрестности рассматриваемой точки тела. В частности, для единичного волокна вдоль оси x (вектор i, координаты: 1, 0) получим [ Di ]=[ D ]
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.005 с.) |
 ; иногда принимают обратную
; иногда принимают обратную  ; очевидно, что оператор этой функции (назовем его В) обратен аффинору А и сам является аффинором
; очевидно, что оператор этой функции (назовем его В) обратен аффинору А и сам является аффинором ,
,  . (3.22)
. (3.22) ,
,
 (3.23)
(3.23) .
. и
и  не являются единичными, их отличие от единицы характеризует степень деформирования, поэтому вводят тензоры
не являются единичными, их отличие от единицы характеризует степень деформирования, поэтому вводят тензоры

 (3.24)
(3.24)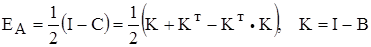 (3.25)
(3.25) . (3.26)
. (3.26) дает всю необходимую информацию о деформированном состоянии, хотя вычислить по ним линейные и угловые деформации не очень просто. Это неудобство частично компенсируется тем, что не возникает проблема факторизации: перемножение
дает всю необходимую информацию о деформированном состоянии, хотя вычислить по ним линейные и угловые деформации не очень просто. Это неудобство частично компенсируется тем, что не возникает проблема факторизации: перемножение  Обобщение состоит в том, что аргументом считается вектор l 0, характеризующий не только длину, но и направление волокна в малой окрестности рассматриваемой точки тела, а функцией является вектор разности
Обобщение состоит в том, что аргументом считается вектор l 0, характеризующий не только длину, но и направление волокна в малой окрестности рассматриваемой точки тела, а функцией является вектор разности Естественно, что для различно ориентированных волокон эти величины различны. Если в окрестности интересующей нас точки тела рассмотреть пучок единичных волокон с общим началом, то их концы лягут на окружность (мы пока ограничимся деформированием в одной плоскости) радиуса 1. Из линейности функции (3.27) следует, что в деформированном состоянии начало этих волокон перейдет, возможно, в новую точку, а концы образуют эллипс (рис.3.5). Полуоси эллипса показывают, какие волокна получили наибольшую и наименьшую деформации и каковы именно эти значе-ия (e1,e2). Эти направления и деформации называют главными.
Естественно, что для различно ориентированных волокон эти величины различны. Если в окрестности интересующей нас точки тела рассмотреть пучок единичных волокон с общим началом, то их концы лягут на окружность (мы пока ограничимся деформированием в одной плоскости) радиуса 1. Из линейности функции (3.27) следует, что в деформированном состоянии начало этих волокон перейдет, возможно, в новую точку, а концы образуют эллипс (рис.3.5). Полуоси эллипса показывают, какие волокна получили наибольшую и наименьшую деформации и каковы именно эти значе-ия (e1,e2). Эти направления и деформации называют главными. (3.27')
(3.27')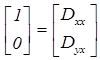 .
.  Из рис.3.6 видно, что первая проекция вектора Di, – Dxx – представляет деформа-цию волокна i, а вторая – поворот (в направлении оси y, то есть против часовой стрелки). Аналогично, второй столбец матрицы дисторсии представляет поворот единичного волокна j в направлении оси x (то есть по часовой стрелке) и деформацию этого волокна (рис. 3.6). Таким образом, зная
Из рис.3.6 видно, что первая проекция вектора Di, – Dxx – представляет деформа-цию волокна i, а вторая – поворот (в направлении оси y, то есть против часовой стрелки). Аналогично, второй столбец матрицы дисторсии представляет поворот единичного волокна j в направлении оси x (то есть по часовой стрелке) и деформацию этого волокна (рис. 3.6). Таким образом, зная  изменение всего двух волокон, мы имеем всю матрицу дисторсии и возможность найти изменения любых волокон из выражения (3.27¢).
изменение всего двух волокон, мы имеем всю матрицу дисторсии и возможность найти изменения любых волокон из выражения (3.27¢).


