
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
H. 3. 10 простейшие модели физических (механических) свойств среды. Закон гука
Механика, как отмечалось, объединяет три стороны: геометрия (движение), динамика (силы) и “физика” - свойства сред. В разделе II для простейшего случая Однородного НДС рассмотрены две стороны; сейчас, для того же однородного НДС познакомимся с “физикой”, характеризующей связь между напряжениями и деформациями тела (а через эту связь определяется и связь между силами и смещениями среды). Классической основой для рассмотрения “физики” является закон Гука. Естественно, это идеализация (как и другие модели свойств); это следует иметь в виду, когда мы будем сталкиваться с какими-либо несоответствиями физическим наблюдениям или даже очевидности. Записать закон линейной связи между тензорами напряжений и деформаций значительно проще, чем в нем разобраться. Начнем с легкого:
Обратим внимание, что если Из тензорного анализа закона Гука видим, что
Из симметрии
Таким образом, из 81 квадриады, составляющей произвольный четырехвалентный тензор, независимых оказывается не более 36.
В действительности их всегда еще меньше! Но это связано с одним очень важным свойством самой Среды (с “физикой”): с законом сохранения энергии, который, если задать тензор Доказательство отложим до тензорного анализа, а пока - результат:
Заметим, что если (3.31) мы принимаем для собственного удобства, то сейчас это условие будет выполняться неизбежно, как следствие (3.30) и (3.32). Итого, если посчитать, остается “только” 21 константа упругости, которыми один упругий материал может отличаться от других. Если вспомнить пространство напряжений и деформаций
и у тензора Симметрия (3.32) здесь отображается симметричностью тензора Но еще довольно много констант! Дело, правда, не настолько печально. В действительности мы почти всегда имеем дело с материалами, свойства которых характеризуются определенной пространственной симметрией. Если из куска металла вырезать образцы разных ориентаций, то их испытания обычно показывают одинаковые свойства. Говорят: металл изотропен. Реакция металла на симметричное воздействие - например, растяжение - должно дать симметричную реакцию. Это накладывает довольно сильные ограничения на тензор
I. 3.10.1. Изотропное тело Тензор Довольно просто убедиться, что нет ничего изотропного кроме единичного тензора Из этого материала можно получить три тензора
причем первый из них - нужной симметрии, а два другие несимметричны. В этом легко убедиться, умножая на произвольный тензор
Поскольку тензор Зато симметричен тензор
который выделяет из тензора симметричную часть
Для симметричных тензоров Итого - всего-то 2 тензора!
Подставив в 3Г, получим
На первую часть С уравнением (3.33) еще можно работать, но дальше будет труднее (для анизотропных сред). Поэтому попробуем чуть упростить. Вместо тензоров
который, как можно показать (а мы в этом просто убедимся) удовлетворяет условию
Исходя из требования (3.34), быстро находим
И убеждаемся:
Закон Гука сейчас принимает более простой, на наш взгляд, вид:
Этот вид хорош тем, что легко обращается (попробуйте получить тензор
позволяет легко вычислять работу
и вообще удобен. А что в Нетрудно установить:
Из закона Гука следует, что в пространстве
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.151.141 (0.012 с.) |
 .
. и
и  - переменные, то
- переменные, то 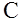 - константа (в этом выражении); по-отдельности
- константа (в этом выражении); по-отдельности  . (3.30)
. (3.30) . (3.31)
. (3.31)
 . (3.32)
. (3.32) , то там закон Гука имеет, очевидно, вид
, то там закон Гука имеет, очевидно, вид

 координат. При этом симметрии (3.30), (3.31) здесь учтены автоматически: умножаем на вектор
координат. При этом симметрии (3.30), (3.31) здесь учтены автоматически: умножаем на вектор  (отвечающий симметричному тензору
(отвечающий симметричному тензору 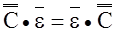 . Отсюда также следует, что независимых координат (констант упругости) у тензора
. Отсюда также следует, что независимых координат (констант упругости) у тензора 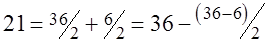 .
. (или шарового
(или шарового  ). На первый взгляд, здесь выделены три направления
). На первый взгляд, здесь выделены три направления  , но мы знаем, что в другом декартовом базисе тензор имеет те же координаты (
, но мы знаем, что в другом декартовом базисе тензор имеет те же координаты ( ). Тензор
). Тензор  - тоже изотропный - не обладает симметрией.
- тоже изотропный - не обладает симметрией.

 произволен, ответ не симметричен, что не отвечает требованию (3.30).
произволен, ответ не симметричен, что не отвечает требованию (3.30).

 - тензор тождественного преобразования.
- тензор тождественного преобразования.
 . (3.33)
. (3.33) деформация влияет не так, как на девиатор! Две разные константы.
деформация влияет не так, как на девиатор! Две разные константы. ,
,  (3.34)
(3.34) .
.


 ):
):

 ?
?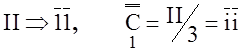 – проецирующий тензор,
– проецирующий тензор, ,
, – тоже проецирующий,
– тоже проецирующий,
 нет изотропных направлений (
нет изотропных направлений ( – независимо от направления
– независимо от направления  ).
).


