
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
The study of the laws of the oscillatory motion by means of a physical pendulumСодержание книги
Поиск на нашем сайте
Accessories: universal pendulum FPM-04, supporting prism, caliper, Objective: To study the vibrational motion of the laws on the example of a physical pendulum, the definition of acceleration of gravity using a pendulum working. Brief details of the theory. Physical pendulum is called a solid, committed under the influence of gravity fluctuations around the horizontal axis without passing through its center of gravity. Let solid (Fig. 5.1) mass m revolves freely about a horizontal axis O perpendicular to the plane of the drawing. Figure 3.1 The physical pendulum. The distance from the center of mass C to О about the same axis
Let us write the equation for the pendulum dynamics of rotational motion. If we denote
At small angles of deviation of the pendulum
or
Introducing the notation
We transform equation (3.3) as follows:
Thus, the small oscillations of a physical pendulum is described by the differential equation (3.5) and its solution has the form:
where Consequently, for small oscillations of the angular deviation of the pendulum varies with time according to a harmonic law (the law sine or cosine). The main property of harmonic oscillations are their frequency, ie, repeatability over the time interval T to obtain the phase increment
value
represents the number of oscillations per unit time is called From equation (3.4.), It follows that for small deviations from the equilibrium position of the frequency of the physical pendulum with respect to the axis of rotation and the distance between the axis of rotation and the center of mass of the pendulum. In accordance with (3.7) during the physical pendulum oscillations with allowance for (3.4) is given by
The value of
called the reduced length of the physical pendulum. By the theorem of Steiner we have:
where
As can be seen from (3.12)
On the point of suspension and the center of the swing To exhibit the property of reciprocity: if the swing of the pendulum about the point K becomes the new center of oscillation point O, and the period of oscillation of a physical pendulum does not change. On this property based definition of acceleration of gravity with the help of the so-called revolving pendulum. Installation and obtain calculation formulas. Revolving pendulum is a steel rod that is rigidly fixed reference prism D and D / (Fig. 5.2.) And the steel weight B. Located between them. And there is another load at one end of the rod, it can move along the scale rod and secured in position. Watch the pendulum, hanging him on a special stand for supporting the prism alternately. By moving the movable weight and achieve the coincidence of periods of oscillations of a pendulum, when the suspension points are the ribs supporting prisms D and D /. We write down the value of the periods Т1 and Т2 at the swing on poles О and О/:
If we find a position of the load A, in which the pendulum oscillation periods Т1 and Т2 about poles О and О/match, the acceleration of gravity is easily determined from the equation (3.13):
where Т=Т1=Т2; In fact, the exact equal periods is difficult to achieve. Therefore formula (. 3.14) and (. 3.15) with (. 3.12) can be written as:
From these equations we have:
from whence
Where
Order of work
Exercise 1: Determination of the gravitational acceleration using a working pendulum 1. Get acquainted with the design of a universal pendulum MTF-04. 2. Strengthen the goods and in the extreme division of the scale (2 cm.) From the prism G (see. Fig. 3.2.) And hang the pendulum of this prism. 3. Turn on the power meter cord to the mains supply. 4. Press the switch "Network", checking whether all indicators show the meter number zero, and if the photoelectric sensor light is on. 5. Reject the pendulum from the equilibrium position at an angle of no more than 5 degrees (the upper end of the rod must be free to counter cross beam sensor) and press "Reset" after the 3-5 full swing. 6. Press "Stop" After counting meter periods of 19 complete oscillations (instrument reading stops at 20). 7. Determine the working period of the pendulum by the formula:
where t-time measured millisekundomerom 20 complete oscillations. 8. To remove the pendulum and set it on the prism О/. 9. On this prism to repeat the experience of claims. 5-7. 10. Move the goods A 1 cm (one division on the web), and repeat the experiment Nos. 5-9. 11. Repeat the 5-10 experience for the division of the rod (6-7 cm). 12. plotted oscillation period T by dividing the rod d (cm), corresponding to the position of cargo A. Find the intersection point of the curves, which corresponds to the position of the load A with the closest match at the swing periods with respect to both poles. The measurement results are recorded in Table 5.1.
Table 5.1
8. Secure the load And found via the chart position. Find 9. suspending the pendulum in one and the other prism (without changing the load position), to determine the appropriate periods of vibration Т1 and Т2. Each period to determine at least 3 times and 50 complete oscillations. 10. Calculate the formula (3.19) is the acceleration of gravity. In this formula, Т1 and Т2 have mean values of three measurements, respectively. 11. Calculate the ratio (3.21.) Measurement error. To determine the need to use the standard error of a certain reliability
where
12. The results of measurements and calculations recorded in Table 3.2.
Table 3.2.
Exercise 2: Defining the free fall with the help of a mathematical pendulum
1. Turn the upper bracket for 1800. 2. Install the lower bracket with a photoelectric sensor at a distance 3. Turn the screw on the top bracket to establish the mathematical pendulum length, with hell on the ball must be at the level of the body features of the photoelectric sensor. 4. Enter a mathematical pendulum in motion, the ball deflecting no more than 50 from the equilibrium position. 5. Press the "Reset" button. 6. After calculating the 19 meter fluctuations press "Stop" (Reading the meter stops at 20). 7. According to the formula (3.22) to determine the period of oscillation of the mathematical pendulum. 8. According to the formula (3.16) to calculate the acceleration of gravity. 9. Ensure that the length of the Control questions 1. What body is called a physical pendulum? 2. Write down the equation of motion of a physical pendulum. 3. What is the period of oscillation of a physical pendulum? 4. What is the value of the reduced length is called a physical pendulum? What is the physical meaning of the reduced length? 5. Formulate the theorem of Steiner. 6. Under what simplifying assumptions derived a formula of a physical pendulum period (3.9)? 7. What is the essence of the method of working of the pendulum? 8. Tell the design working pendulum used in this paper. Literature 1. Savelyev IV The general course of physics v.1. A.: Science, 1977. 2. sivukhin IV The general course of physics. v.1. M.: Nauka, 1979. 3. Gunners SP The general course of physics. Mechanics. M.: 1975.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.143.18 (0.007 с.) |

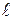 . In the event of the pendulum from the equilibrium position at an angle
. In the event of the pendulum from the equilibrium position at an angle  , a torque which tends to return the pendulum to its equilibrium position. Attributing,
, a torque which tends to return the pendulum to its equilibrium position. Attributing,  torque and angular displacement have opposite signs
torque and angular displacement have opposite signs (3.1)
(3.1) the angular acceleration and
the angular acceleration and 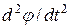 torque across the pendulum of inertia about the axis passing through the point of suspension O by
torque across the pendulum of inertia about the axis passing through the point of suspension O by 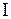 , taking into account (3.1), we obtain
, taking into account (3.1), we obtain (3.2)
(3.2) ; then
; then
 (3.3)
(3.3) , (3.4)
, (3.4) (3.5)
(3.5) , (3.6)
, (3.6) - the amplitude of the oscillations, ie, the greatest angle, which deviates the pendulum:
- the amplitude of the oscillations, ie, the greatest angle, which deviates the pendulum:  - phase fluctuations; constant is a phase value at time t = 0 and is called the initial phase.
- phase fluctuations; constant is a phase value at time t = 0 and is called the initial phase. . This time period is called the period T
. This time period is called the period T (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10) (3.11)
(3.11) - the moment of inertia about an axis through the center of gravity (see Figure 3.1...) and parallel to the swing axis O; l - distance between the axes. Then, the reduced length of the physical pendulum is equal to
- the moment of inertia about an axis through the center of gravity (see Figure 3.1...) and parallel to the swing axis O; l - distance between the axes. Then, the reduced length of the physical pendulum is equal to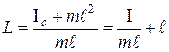 (3.12)
(3.12) . If postpone along the line segment OS OK (Fig. 3.1.), Is equal to L, the resulting point K is called the center of oscillation. Then the pendulum with a mass concentrated at the point K (this is called a mathematical pendulum) will fluctuate with the same period as that of the physical pendulum, which is equal to the period
. If postpone along the line segment OS OK (Fig. 3.1.), Is equal to L, the resulting point K is called the center of oscillation. Then the pendulum with a mass concentrated at the point K (this is called a mathematical pendulum) will fluctuate with the same period as that of the physical pendulum, which is equal to the period (3.13)
(3.13) (3.14.)
(3.14.) (3.15.)
(3.15.) (3.16.)
(3.16.) those. In this case, the reduced length of the physical pendulum is equal to the distance between the supports О and О/.
those. In this case, the reduced length of the physical pendulum is equal to the distance between the supports О and О/. (3.17)
(3.17) (3.18)
(3.18)
 (3.19)
(3.19) (3.20) The error can be found from the relation
(3.20) The error can be found from the relation (3.21) Where
(3.21) Where 
 (3.22)
(3.22) and
and 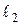 distance. To do this, put the pendulum horizontally on a special supporting prism and achieve its equilibrium. Mark the balance point and measure the desired distance
distance. To do this, put the pendulum horizontally on a special supporting prism and achieve its equilibrium. Mark the balance point and measure the desired distance  , ie
, ie (3.23.)
(3.23.) -the coefficient of the Student; the mean square error is equal to (3.24).
-the coefficient of the Student; the mean square error is equal to (3.24). (3.24.)
(3.24.)

 м/с2
м/с2
 (the length of the distance between the prisms О and О/ defined in Exercise 1).
(the length of the distance between the prisms О and О/ defined in Exercise 1).


