
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Study of the laws of motion rotary solidСодержание книги
Поиск на нашем сайте
Accessories: pendulum Oberbeck MTF-06 cargo caliper. Objective: To study the rotational motion of a solid body of laws; determination of the moment of inertia of the pendulum Oberbeck experimentally and theoretically. Brief details of the theory. The solid body can be regarded as a system of material points, the distance between them always. The rotational motion of a solid body is called a motion in which the trajectories of all points of the body are concentric circles centered on the same straight line, called the axis of rotation.
Let the solid body rotating around a fixed axis in the frame of reference 00 /, committed during The corresponding angle of rotation is characterized by
characterizes the rate of change of the angle of rotation is called the angular velocity. vector direction coincides
vector module is
where R-radius of the circle, which describes the point under consideration. Vector pointing towards the rotation tangential to the path and is perpendicular to the plane in which lie both.
When uneven rotation value changes over time, and the time interval is incremented. value
Characterizing the speed of change over time of the angular velocity, angular acceleration is called the rotating body. If the body is rotated about a fixed axis, the vector is directed along this axis; in the same direction as that at the accelerated When the rotational motion of the body change its kinematic and dynamic quantities depend on acting on the body of the rotational torque and the moment of inertia of the body. The moment of force is
The direction of the vector
where R- shoulder vector The moment of inertia
Moment of inertia of a body is equal to the sum of the moments of inertia of all the material points of the body
where
Consequently, the moment of inertia can be written as:
If the density of the body is constant, it can be taken outside the sum of:
Relations (2.10) and (2.11) are approximate, and the more accurate the smaller the elementary volumes
The moment of inertia is a physical quantity that characterizes the inertia body when changing their angular velocity under the influence of torque. In cases where the body axis of rotation is arbitrary, the calculation of the moment of inertia is considerably simplified if we use the theorem of Steiner: moment of inertia
The Basic Law of the dynamics of rotational motion of a rigid body about a fixed axis z is written as follows:
Mz where - the total time of all external forces about the axis of rotation.
|
||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.007 с.) |

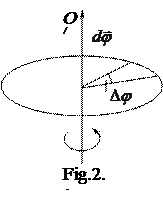

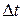 an infinitesimal rotation
an infinitesimal rotation 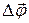 (Figure 2.1).
(Figure 2.1).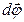 a vector whose magnitude is equal to the
a vector whose magnitude is equal to the 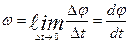 (2.1)
(2.1)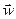 with the direction of the vector. The unit of the angular velocity - radians per second (rad / s).
with the direction of the vector. The unit of the angular velocity - radians per second (rad / s).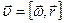 (2.2)
(2.2)
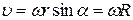 (2.3)
(2.3)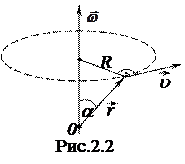
 (2.4)
(2.4)
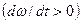 and rotated in the opposite direction - in slow rotation
and rotated in the opposite direction - in slow rotation  . The unit of angular acceleration - radians per second squared (rad / s2).
. The unit of angular acceleration - radians per second squared (rad / s2).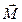 a vector quantity equal to the radius vector bringing -
a vector quantity equal to the radius vector bringing - 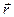 ,vector drawn from O to the point of application of force A, a vector force
,vector drawn from O to the point of application of force A, a vector force 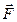
 (2.5)
(2.5)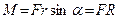 (2.6)
(2.6)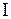 of the material point with respect to any axis is the product of its mass in the square of the distance from the
of the material point with respect to any axis is the product of its mass in the square of the distance from the  axis of rotation:
axis of rotation: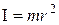 (2.7)
(2.7) (2.8)
(2.8)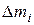 - an elementary mass contained in the volume - th particle. The unit is the product of the mass
- an elementary mass contained in the volume - th particle. The unit is the product of the mass 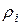 on the corresponding volume element
on the corresponding volume element 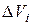 :
: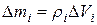 (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11)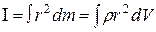 (2.12)
(2.12)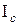 with respect to the geometrical axis, and the works of body weight to the square of the distance
with respect to the geometrical axis, and the works of body weight to the square of the distance 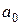 between the axles:
between the axles: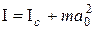 (2.13)
(2.13) (2.14)
(2.14)


