
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Evaluation of the accuracy of the result of repeated direct measurements
Let the repeated measurement
Each individual measurement differs from the arithmetic mean by
The deviation is called The absolute error From experience we know that the probability of error is smaller, the more it. Additionally, if a very large number of measurements
The less
Consequently,
The square root of the variance measurement is called the mean square error
If, instead of the expression (1.1.6) to substitute the value of the equation (1.1.2), then
In the expression (1.1.7) includes the value
Or
Estimates of variance Measurement processing task is to determine the range of up It follows from the theory of errors that a large number of measurements In cases where the number of measurements is small, there are no conditions for the existence of a strict statistical regularities that underlie the determination of random errors. This leads to the fact that the values of the standard deviation of the average Sa, calculated from (1.1.9) is not accurate and the more inaccurate the smaller number of measurements
The measurement results can not be compared values dissimilar to each other by their absolute errors. For comparison, the measurement accuracy of these values is entered relative error - the ratio of absolute error to the mean value of the measured value.
According to the relative error is convenient to compare the results of measurements of similar values. Values Ctyudenta coefficients.
Table 1.1.1
Order of work
As an example, consider the processing of the results of measurements of the oscillation period of a simple pendulum (mathematical pendulum is called the body suspended on a weightless and inextensible thread, which is much greater than its size). 1. Use the stopwatch to measure the time tі 30 oscillations of a pendulum. The measurements were repeated n times (n is given by the teacher). 2. According to the formula
calculate the period of oscillation. 3. Definitions sredngo arithmetic mean value of the oscillation period
4. According to the formula (1.1.9) to find the standard deviation of T. 5. From the table to find the value of the Student's coefficient corresponding to reliability, said the teacher (Student coefficient table is available in the laboratory). 6. When the values found and the formula (1.1.10) to calculate the absolute error. 7. Calculate the relative error by the formula (1.1.12). 8. The results of measurement and computation recorded in the table Table (1.1.2)
Control questions 1. What kinds of measurements are divided and associated errors. 2. How is the absolute error. 3. What is the Student factor is introduced. 4. What do the confidence interval and confidence level. 5. Why is it necessary to calculate the relative error. 6. What is called a mathematical pendulum. 7. What is called the period of oscillation.
Literature 1. Kassandrova ON, VV Lebedev Processing of observations. M.: Nauka, 1970. 2. Agekyan TA Fundamentals of the theory of errors for astronomers and physicists. M.: Nauka, 1972.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.48 (0.014 с.) |
 of a physical quantity
of a physical quantity  of its values were obtained:
of its values were obtained:  Then, the arithmetic mean of all values obtained, which is the most significant as well
Then, the arithmetic mean of all values obtained, which is the most significant as well =
=  =
=  (1.1.1.)
(1.1.1.) (1.1.2.)
(1.1.2.) absolute error of i - that dimension.
absolute error of i - that dimension. of individual measurements take both positive and negative values.
of individual measurements take both positive and negative values. , the errors are the same magnitude but different in sign occur equally often. Speed reducing the probability of occurrence and its increase is characterized by
, the errors are the same magnitude but different in sign occur equally often. Speed reducing the probability of occurrence and its increase is characterized by  a dispersion of error. It is
a dispersion of error. It is (1.1.3)
(1.1.3) , the less the likelihood of greater in magnitude of random error
, the less the likelihood of greater in magnitude of random error  (1.1.4)
(1.1.4) (1.1.5)
(1.1.5) (1.1.6)
(1.1.6) (1.1.7)
(1.1.7) . The very magnitude
. The very magnitude 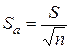 (1.1.8)
(1.1.8) (1.1.9)
(1.1.9) are marginal, fair, just
are marginal, fair, just  , ie, at large
, ie, at large  to
to  , which concluded with a probability of the true
, which concluded with a probability of the true  value of the measured value. The interval from
value of the measured value. The interval from  to
to  of 95 measurement values were obtained, without departing from its scope. Of course, the greater reliability is required, the more turns the corresponding confidence interval, and conversely, the larger the confidence interval is given, the more likely that the measurement results will not go beyond it.
of 95 measurement values were obtained, without departing from its scope. Of course, the greater reliability is required, the more turns the corresponding confidence interval, and conversely, the larger the confidence interval is given, the more likely that the measurement results will not go beyond it. to
to  68%, and the interval from
68%, and the interval from  to
to  is 95%. When submitting any of the measured values of the main lead and the confidence interval of the probability of corresponding to this interval.
is 95%. When submitting any of the measured values of the main lead and the confidence interval of the probability of corresponding to this interval. (1.1.11)
(1.1.11) (1.1.12)
(1.1.12)


 (1.1.13)
(1.1.13)
 Тi с
Тi с







