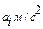Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Installation and obtain calculation formulasСодержание книги
Поиск на нашем сайте Pendulum Oberbeck FPM-06, called on the instrument, is complex, providing experimental determination of laws of rotational dynamics of rigid body motion. The pendulum used in the device is an inertial wheel in the form of crosses (Fig.2.4). On chertyreh mutually perpendicular rods can move loads. The horizontal axis of the cross there is a two-stage drive with radii Rm and Rb, which is wound thread. One end of the thread is attached to the disc, and the second end of the thread is suspended load R. Under the influence of the falling load P, the thread unwinds from the disk and causes a rotational movement uniformly accelerated crosses. If you drop the load will be accelerated and then the pendulum will rotate with angular acceleration
from whence
where R-radius pulley.
Figure 2.4. pendulum Oberbeck If we denote by T the thread tension force, the rotational torque in this study will be determined by the formula
Force T can be found from the equations of motion P:
from (2.18)
Substituting (2.19) into (2.17), we have a working formula for the torque:
The moment of inertia of the whole system - the pendulum with weights on the bars - can be calculated by the following formula (derivation of the formula given in the appendix):
where I0-total moment of the two-stage drive inertia axes and bush frog (the value indicated on the device), Order of work 1. Move the flexible arm to the specified height h teacher. Set it so that loads falling freely pass through the middle of the working window of photoelectric sensors. 2. Set the movable weight on the rods on said teacher division and the distance R from the axis of rotation to the center of the load. 3. Measure the diameter of the disc and a caliper to determine the radii Rb RM small and larger drives. 4. Insert the power cord into the power meter network. Press "Start". 5. Press the "Network", checking whether all indicators show zero meter and all LEDs are lit if both photoelectric sensors. 6. Attach to the thread wound on the disk radius RM, the initial load mass m. 7. Move the load to its highest position by winding the thread on the selected disk, and set the bottom edge of the load precisely with a dash on the housing upper photoelectric sensor and squeeze the buttons "Start". Check whether the lock has occurred. 8. Press the "Reset". Press "Start". 9. Read off the measured value of goods falling time on the way h. 10. Press the "Reset". 11. Measuring repeated 3-5 times and the average value to determine the time of movement of goods by the formula:
where n is the number of executed measurements, ti-time measured value at i-volume measurement, t-time average value of loads along the path h. 12. Calculate the linear acceleration, and in formula (2.15) and the angular acceleration ε formula (2.16). 13. Calculate the torque from the formula (2.20). 14. Repeat steps. 6-12 2-3 cargoes of other masses. 11. According to the calculated values
12. From the graph, determine the moment of inertia of the system 13. Repeat steps 6-16 for selecting Rb radius pulley scale for values and can be plotted on the small and large pulleys in the same 14. Determine the moment of inertia of the system calculated by the equation (2.21). Pendulum inertia 15. Check the convergence of the experimental and theoretical values of the moments of inertia obtained by the ratio of the system:
15. All data and calculation results recorded in Table 2.1
Table 2.1
Control questions 1. What is the rotational motion of a solid body? 2. Identify and write the formula of angular velocity and angular acceleration. Specify their areas and units. 3. What is the relationship between the linear and angular velocity? As the linear velocity is directed? 4. What is called the moment of inertia of the material point and the body? What characterizes it? 5. Formulate the theorem of Steiner. Write a formula. 6. What is the torque? What force creates a torque? As directed vector torque? 7. Write and explain the fundamental law of dynamics of rotational motion? 8. Describe applied in this study unit. Which part of the system moves forward, what is rotated? 9. Is the line
Literature 1. Savelyev IV Zhalpy physics courses. A.: Mektep, 1977, vol.1. 2. Frisch SE, AV Timoreva Zhalpy physics courses. Volume 1, A.: Mektep 1971. 3. DV sivukhin The general course of physics. Vol.1, M.: Nauka, 1979.
Job number 4
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.89.150 (0.008 с.) |

 . By measuring the time t, within which the load F falls from the rest is the distance h, you can find
. By measuring the time t, within which the load F falls from the rest is the distance h, you can find  the acceleration of the load:
the acceleration of the load: (2.15)
(2.15) which is related to the ratio of the angular acceleration
which is related to the ratio of the angular acceleration
 (2.16)
(2.16) (2.17)
(2.17) (2.18)
(2.18) (2.19)
(2.19) (2.20)
(2.20)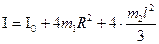 (2.21)
(2.21) - the length of the cross bar;
- the length of the cross bar;  - the moment of inertia of moving cargo crossings;
- the moment of inertia of moving cargo crossings;  - the moment of inertia of the cross without the goods; R-distance from the axis of rotation to the load center, m1-weight of one rolling cargo, m2-weight rod without load.
- the moment of inertia of the cross without the goods; R-distance from the axis of rotation to the load center, m1-weight of one rolling cargo, m2-weight rod without load. , (2.22)
, (2.22) and
and  plotted on the ordinate
plotted on the ordinate  , whose value
, whose value 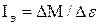 and the moment of friction force Mtr to the axis of rotation, finding ways which are shown in Fig. 2.5
and the moment of friction force Mtr to the axis of rotation, finding ways which are shown in Fig. 2.5 and
and  torque without cylindrical weights indicated on the unit.
torque without cylindrical weights indicated on the unit. (2.23)
(2.23)