
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Evaluation of the accuracy of results of indirect measurementsСодержание книги
Поиск на нашем сайте
In general, the target value is a function of one or more variables. For example, the electric current in Let the unknown quantity A is a function of the measured value x: A=¦(х) (1.2.3.) The absolute error of the measured value of A leads to mistakes
We restrict ourselves to two terms of this series, as the other members are infinitesimal of a higher order. Then:
According to (1.2.3), we have:
That is a function of the absolute error is equal to the product of the derivative of this function, the absolute error of the argument. Let the unknown quantity A depends on n variables:
Then the differential of a function of several variables can be expressed as:
where Instead of the absolute error is often convenient to calculate the relative error. Relative error can be represented as:
When the function ¦ (
or
The overall result is written as:
1.Prologarifmirovat calculation formula. 2.Vzyat total differential of both sides. 3.Please replace the sign of d to 4.Po formula (1.2.11.) To find the relative error. 5. Knowing A = ± ΔA (1.2.13). 6. The result is written in the form (1.2.12.). The absolute error of the result should be rounded to one significant figure, but the result of the measurement rounded to the order in which the error begins. As an example, consider the calculation of the volume of a sphere. He is
where R-radius of the sphere. Directly measured R-radius of the sphere. The volume of a sphere V- value of indirectly measured. Let R measured with calipers, the price of which is 0.1 mm division. The measurement result based on the error has the following meaning:
Now calculate the volume V. It is equal to V = 45806,5mm3. Next error is calculated as
As for the error, it can be done any number of small, if you take a sufficient number of characters. Then they can be neglected. Finally:
and Absolute error necessarily result should be rounded to one significant figure, and the measurement result is rounded to-order (in this example, V), where the error begins. In this case, to be rounded up to hundreds. The final test result written as follows:
Order of work
It is necessary to calculate the density of regular geometric body shapes (cuboid, cylinder, sphere). 1. To determine body mass (box, cylinder, sphere). Record it with the precision of measurements. 2.Find body dimensions using calipers (the same body). Determine error. 3.Opredelit body density measured using the following relations: a) a rectangular parallelepiped
where m-mass, h-height, b-width, the length of the box b) for the cylinder
where m-mass, R-radius of the base, h-height of the cylinder; c) for the ball
where mass m-, R- radius of the sphere. 4. According to the formula (1.2.11) to calculate the relative error, ie. E.: a) a rectangular parallelepiped
b) the length of the cylinder
c) for the ball
5. According to the formula (1.2.13) to calculate the absolute error. The results are rounded based on measurement errors. 6. The final result is written in the form (1.2.12) 7. The results of measurements and calculations recorded in table 1.2.1
Table 1.2.1
Control questions 1. As determined by the instrument error? What is the accuracy of the readings? Specify price vernier division. 2. How are the absolute errors of the physical constants with non-periodic infinite fractions? 3. How is the accuracy of the indirect measurement? 4. Get a formula assessing the relative errors for functions of the form:
where a, b, g - some constants. Literature 1. A. Seidel Elementary estimates of measurement errors. L.: Science, 1974. 2.Kassandrova ON, VV Lebedev Processing of observations. M.: Nauka, 1970. 3.Agekyan TA Fundamentals of the theory of errors for astronomers and physicists. M.: Nauka, 1972. Job number №2
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.67.189 (0.006 с.) |

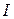 a conductor is a function of the potential difference at the ends of the conductor
a conductor is a function of the potential difference at the ends of the conductor 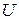 , and the conductor resistance R. Therefore, for the determination of this magnitude must first conduct a series of direct measurements of auxiliary variables, and then, using the formulas of physical laws to calculate the required amount. In this case we speak of indirect measurements.
, and the conductor resistance R. Therefore, for the determination of this magnitude must first conduct a series of direct measurements of auxiliary variables, and then, using the formulas of physical laws to calculate the required amount. In this case we speak of indirect measurements. . Decomposition of the right side in a Taylor series gives:
. Decomposition of the right side in a Taylor series gives: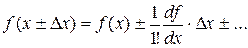 (1.2.4.)
(1.2.4.)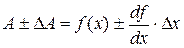 (1.2.5.)
(1.2.5.)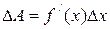 (1.2.6.)
(1.2.6.)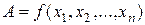 (1.2.7.)
(1.2.7.)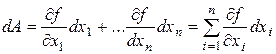 (1.2.8.)
(1.2.8.)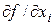 - the partial derivatives. In calculating the last
- the partial derivatives. In calculating the last  arguments except considered constant
arguments except considered constant 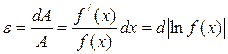 (1.2.9.)
(1.2.9.) (1.2.10)
(1.2.10)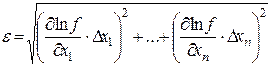 (1.2.11.)
(1.2.11.)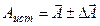 (1.2.12.) Thus, to determine the error of indirect measurements following results:
(1.2.12.) Thus, to determine the error of indirect measurements following results: , sign all minus signs on the plus sign.
, sign all minus signs on the plus sign. , determine the absolute error:
, determine the absolute error: (1.2.14.)
(1.2.14.)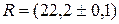 мм (1.2.15.)
мм (1.2.15.) :
: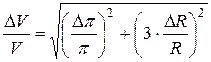 (1.2.16.)
(1.2.16.)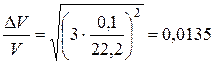 (1.2.17.)
(1.2.17.)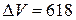 мм3,
мм3, 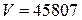 мм3.
мм3.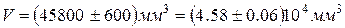 (1.2.18.)
(1.2.18.)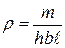 (1.2.19)
(1.2.19)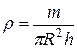 (1.2.20)
(1.2.20)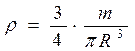 (1.2.21)
(1.2.21)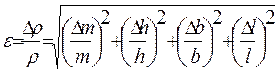 (1.2.22)
(1.2.22)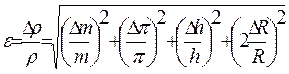 (1.2.23)
(1.2.23) (1.2.24)
(1.2.24) ;
; 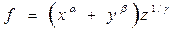 ;
;


