
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра высшей математики и информационных технологийСтр 1 из 3Следующая ⇒
Кафедра высшей математики и информационных технологий А.А.Фатхуллина МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1 ПО МАТЕМАТИКЕ Нижнекамск – 2014 СОДЕРЖАНИЕ 1. Введение. 3 2. Общие требования к выполнению контрольной работы.. 5 3. Теоретические сведения к выполнению контрольной работы.. 5 3.1. Матрицы. Операции над матрицами. 5 3.2. Определители второго и третьего порядков. 8 3.3. Обратная матрица. 10 3.4. Система линейных алгебраических уравнений (СЛАУ) 11 3.5. Векторы и операции над ними. 15 3.6. Уравнение прямой на плоскости. 17 3.7. Комплексные числа. 21 3.8. Вычисление пределов функции. 26 3.9. Непрерывность функции. 29 3.10. Производная. 32 3.11. Исследование функции на экстремум. 34 3.12. Неопределенный интеграл. 39 3.13. Определенный интеграл. 45 4. Образец выполнения контрольной работы.. 48 5. Задания контрольной работы.. 62 6. Учебно-методическое обеспечение. 72
Данные методические указания адресованы студентам заочных форм обучения (сокращенные сроки) по направлению «Технология продукции и организации общественного питания» при выполнении контрольной работы №1 по дисциплине «Математика». Эта работа полностью соответствует ФГОС ВПО по направлению «Технология продукции и организации общественного питания». Студенты заочной формы обучения довольно часто испытывают серьезные затруднения при выполнении и грамотном оформлении контрольной работы. Настоящее учебно-методическое пособие призвано помочь студентам самостоятельно выполнить задания контрольных работ и правильно их оформить. Данные методические указания состоят из следующих основных частей: общих требований к выполнению контрольной работы, теоретических сведений необходимых для выполнения контрольной работы, образца решения нулевого варианта контрольной работы и 10 вариантов заданий контрольной работы №1 по дисциплине «Математика» для направления «Технология продукции и организации общественного питания». Раздел «Теоретические сведения к выполнению контрольной работы» содержит необходимый минимум сведений из курса математики, требуемый для выполнения предлагаемых заданий. Этот теоретический материал включает в себя все необходимые определения, утверждения и формулы. По каждой теме приводятся примеры, в которых подробно описывается весь ход решения. Образец решения нулевого варианта контрольной работы призван помочь студентам в дальнейшей отработке навыков решения задач из курса «Математика» и в грамотном оформлении собственной работы. Предлагаемые варианты заданий контрольных работ полностью соответствуют объему изучаемого материала курса математики. Все это даст возможность студентам заочных форм обучения качественно выполнить контрольную работу.
Целями освоения дисциплины «Математика» являются изучение математики с элементами аналитической геометрии и разделов математического анализа, приобретение навыков использования математического универсального понятийного аппарата и широкого арсенала технических приемов при построении математических моделей различных экономических закономерностей и процессов и прогнозировании развития экономики. Достижение этих целей обеспечивает выпускнику получение высшего профессионально профилированного (на уровне бакалавра) образования. Изучение дисциплины направлено на формирование компетенций, позволяющих применять базовые математические знания для решения профессиональных задач. Данные методические указания способствуют развитию следующих профессиональных компетенций студентов обучающихся по направлению «Технология продукции и организации общественного питания»: – способен использовать законы и методы математики, естественных, гуманитарных и экономических наук при решении профессиональных задач (ПК-1); – использует основные законы естественнонаучных дисциплин в профессиональной деятельности, применяет методы математического анализа и моделирования, теоретического и экспериментального исследования. Умеет использовать нормативные правовые документы в своей (ПК-3); – способен измерять и составлять описание проводимых экспериментов, подготавливать данные для составления обзоров, отчетов и научных публикаций; владеет статистическими методами и средствами обработки экспериментальных данных проведенных исследований (ПК-32).
Для достижения порогового уровня сформированности данных компетенций необходимо: – решить задания контрольной работы 1, 3, 4(а), 6(а, б, в), 7(а), 8(а, б), 10(а,б), 12(а,б,в), 13 и 14, то есть все задания контрольной работы, кроме заданий 2, 4(б) и 7(б), 8(в), 9 и 11. – уметь объяснять ход решения предлагаемых задач, знать правила и принципы, на которых основано это решение; – уметь исправлять ошибки, допущенные в ходе решения задач. Количество верно выполненных заданий должно быть не менее 60 %, то есть допускается не более 6 заданий из 16, в которых допущены ошибки. Дополнительные задания, предлагаемые студентам, претендующим на овладение повышенным уровнем сформированности компетенций, помечены значком * (звездочка). Для достижения повышенного уровня сформированности этих компетенций необходимо: – самостоятельно верно решить все задания контрольной работы; – знать теоретические сведения, на которых основано решение данных заданий; – уметь обосновывать выбор метода решения предлагаемых задач; – уметь формулировать самостоятельно выводы по полученным данным и их интерпретировать.
2. Общие требования к выполнению контрольной работы
Приступая к выполнению контрольной работы по математике необходимо изучить теоретический материал и разобрать решения заданий нулевого варианта приведенных в образце выполнения контрольной работы. Только после этого рекомендуется приступать к решению контрольной работы. Студент выполняет вариант контрольной работы, соответствующий последней цифре номера его зачетной книжки (цифре 0 соответствует номер 10). Работа с чужим вариантом не засчитывается. Контрольная работа выполняется вручную в тетради, страницы которой имеют поля для замечаний преподавателя. Последовательность решения задач должна соответствовать последовательности заданий контрольной работы. Перед решением задачи необходимо переписать ее условие. Титульный лист выполняется на компьютере и оформляется по примеру, приведенному в приложении. Выполненная и оформленная контрольная работа должна быть представлена на кафедру высшей математики Института экономики, управления и права (г. Казань) не позднее, чем за 15 дней до начала сессии.
Обратная матрица
Матрица
Матрица Алгоритм вычисления обратной матрицы: 1. Вычислить определитель матрицы 2. Вычислить транспонированную матрицу 3. Вычислить алгебраические дополнения матрицы 4. Вычислить обратную матрицу по формуле:
5. Проверить правильность вычислений по формуле (1). Выполнение данного пункта не является обязательным. Пример. Вычислить обратную матрицу
Решение. 1. Вычислим определитель данной матрицы.
2. Вычислим транспонированную матрицу
3. Вычислим алгебраические дополнения матрицы
4. Вычислим обратную матрицу:
Основные понятия Рассмотрим систему из m линейных уравнений с n переменными:
где Совокупность чисел Система, не имеющая решений, называется несовместной. Система, имеющая решения называется совместной. Совместная система, имеющая единственное решение называется определенной. Совместная система, имеющая более одного решения называется неопределенной. Выпишем коэффициенты при переменных в системе (2) в виде матрицы:
Матрица Выписав из системы все переменные, получим матрицу-столбец переменных:
Выписав все свободные члены, получим матрицу-столбец свободных членов:
Матрица
называется расширенной матрицей системы. Формулы Крамера Рассмотрим систему (2), в которой число уравнений равно числу переменных, то есть Если определитель матрицы системы
где
Формулы (3) называются формулами Крамера. Пример. Решить систему линейных уравнений:
Решение. Решим систему линейных уравнений с помощью формул Крамера. Составим определитель матрицы системы уравнений. Для этого выпишем коэффициенты при переменных
Заменив первый столбец определителя
Заменив второй столбец определителя
По формулам Крамера находим:
Ответ:
Метод Гаусса
Рассмотрим решение системы (2) методом Гаусса (методом последовательного исключения переменных). Метод Гаусса состоит из прямого и обратного хода. Прямой ход. Выпишем расширенную матрицу системы (2) и приведем матрицу к ступенчатому виду, то есть к виду, для которого выполняются условия: 1) все ненулевые строки (имеющие, по крайней мере, один ненулевой элемент) располагаются над всеми чисто нулевыми строками; 2) ведущий элемент, то есть первый ненулевой элемент строки при отсчёте слева направо каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.
Каждую прямоугольную матрицу с помощью элементарных преобразований можно привести к ступенчатому виду. Элементарные преобразования матрицы – это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, заданной с помощью этой матрицы. К элементарным преобразованиям матрицы относится: 1) умножение любой строки на числовой коэффициент 2) прибавление к какой-либо строке другой строки, умноженной на числовой коэффициент; 3) перестановка местами любых двух строк. Обратный ход. Вернемся от расширенной матрицы ступенчатого вида к системе уравнений, которая соответствует этой матрице. Затем начиная с последних по номеру переменных, последовательно найдем все переменные. Пример. Решить систему линейных уравнений:
Решение. Решим эту систему уравнений методом Гаусса.
Прокомментируем каждый шаг алгоритма: 1-й шаг: умножаем первую строку на (-2) и прибавляем к третьей строке. В результате получим в первом столбце все нули, кроме верхнего элемента. 2-й шаг: умножим вторую строку на 3-й шаг: умножим вторую строку на 5 и прибавим к третьей строке. В результате мы получим расширенную матрицу ступенчатого вида. Далее от полученной расширенной матрицы вернемся к соответствующей ей системе уравнений:
Отсюда, из третьего уравнения найдем Ответ:
Векторы и операции над ними
Вектором называется направленный отрезок, который можно перемещать параллельно самому себе. Векторы могут обозначается несколькими способами. Например, Длиной вектора Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Вектор, длина которого равна нулю, называется нуль-вектором. Нуль-вектор обозначается Произведением вектора Противоположным вектором называется вектор
Разностью двух векторов Введем понятие координат вектора. Для этого совместим начало вектора Пусть точка Суммой векторов Разностью векторов Произведением вектора Длина вектора Скалярным произведением векторов Если вектора Заметим, что скалярный квадрат вектора равен квадрату его длины: Угол между векторами
Пример. Даны два вектора Решение. Вычислим косинус угла между этими векторами: Ответ: Комплексные числа
Определение. Числа вида Число Замечание. В электротехнике, где буква Алгебраические действия над комплексными числами выполняются по формулам:
Пример. Пусть
Вычисление пределов функции
Пусть функция В этом случае пишут: В самой точке При вычислении пределов применяются следующие теоремы: I. Если точка II. Если существуют конечные пределы 1. 2. 3. 4. Полагают, что Вычисление предела Пример. Найти Решение. Используя теоремы о пределах, получим:
Ответ: 7. Для раскрытия неопределенности
где В квадратном трёхчлене В выражении Пример. Найти Решение. При подстановке в выражение, стоящего под знаком предела предельного значения
Ответ: Пример. Найти Решение. Имеем неопределенность вида
Ответ: 0. Пример. Найти Решение. При подстановке вместо переменной Пример. Найти Решение.При подстановке вместо переменной В результате получим
Для вычисления пределов часто используются первый замечательный предел:
и второй замечательный предел:
или
а также их следствия:
При вычислении пределов также могут использоваться следующие известные пределы:
Непрерывность функции
Функция
В определении предела В определении непрерывности пределом Непрерывность 1) существование значения функции 2) существование предела функции 3) значение функции Если какое-либо из этих условий будет нарушено в заданной точке, то такая точка называется точкой разрыва. Пример. Дана функция 1) 2) 3) Теорема. Сумма, разность, произведение, частное двух непрерывных в точке функций (функция, стоящая в знаменателе
Определение.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.168 (0.146 с.) |
 называется обратной по отношению к квадратной матрице
называется обратной по отношению к квадратной матрице  , если выполняется равенство:
, если выполняется равенство: (1)
(1) .
. .
. .
.
 .
. ;
; 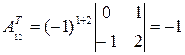 ;
;  ;
; ;
;  ;
;  ;
; ;
;  ;
;  .
. .
. (2)
(2) – коэффициенты при переменных,
– коэффициенты при переменных,  – свободные члены уравнений.
– свободные члены уравнений. называется решением системы (2), если при их подстановке каждое уравнение системы обращается в верное равенство.
называется решением системы (2), если при их подстановке каждое уравнение системы обращается в верное равенство. .
. называется матрицей системы.
называется матрицей системы. .
. .
.
 . В этом случае матрица системы будет квадратной, а ее определитель называется определителем системы.
. В этом случае матрица системы будет квадратной, а ее определитель называется определителем системы.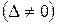 , то система имеет единственное решение, которое определяется по формулам:
, то система имеет единственное решение, которое определяется по формулам: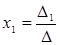 ,
,  , …,
, …,  , (3)
, (3)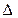 − определитель матрицы системы,
− определитель матрицы системы, − определитель, получаемый из определителя
− определитель, получаемый из определителя  - го столбца столбцом свободных членов.
- го столбца столбцом свободных членов.
 ,
,  и
и  в определитель и вычислим его по «правилу треугольника»:
в определитель и вычислим его по «правилу треугольника»:

 Заменив третий столбец определителя
Заменив третий столбец определителя 
 ,
,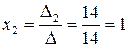 ,
,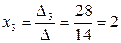 .
.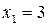 ,
,  ,
,  .
. .
. ;
;
 Выпишем расширенную матрицу и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выпишем расширенную матрицу и с помощью элементарных преобразований приведем ее к ступенчатому виду: 


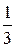 .
.
 . Подставляя полученное значение во второе уравнение, найдем
. Подставляя полученное значение во второе уравнение, найдем  . Подставляя вместо
. Подставляя вместо  и
и  .
. .
.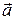 либо a, или
либо a, или  , где точка
, где точка  означает начало вектора, а точка
означает начало вектора, а точка  – конец вектора.
– конец вектора. называется число, равное длине отрезка
называется число, равное длине отрезка  , изображающего вектор. Длина вектора обозначается
, изображающего вектор. Длина вектора обозначается  .
. .
. называется вектор
называется вектор  , имеющий длину
, имеющий длину  , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора  , и противоположно ему, если
, и противоположно ему, если  .
. .
.
 Определим понятие суммы двух векторов. Пусть
Определим понятие суммы двух векторов. Пусть  – два произвольных вектора. Возьмем произвольную точку
– два произвольных вектора. Возьмем произвольную точку  и построим вектор
и построим вектор 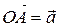 . От точки
. От точки  . Вектор
. Вектор  , соединяющий начало первого вектора с концом второго, называется суммой векторов
, соединяющий начало первого вектора с концом второго, называется суммой векторов  . (см. рис. 1) Это правило сложения векторов называется правилом треугольника.
. (см. рис. 1) Это правило сложения векторов называется правилом треугольника. Также сумму двух векторов можно построить по правилу параллелограмма. Для этого берут произвольную точку
Также сумму двух векторов можно построить по правилу параллелограмма. Для этого берут произвольную точку  и
и  . Далее на этих векторах достраивают параллелограмм
. Далее на этих векторах достраивают параллелограмм  . Диагональ
. Диагональ  является суммой векторов
является суммой векторов  . (см. рис. 3)
. (см. рис. 3) , а точка
, а точка  . Тогда координаты вектора
. Тогда координаты вектора  .
. и
и  является вектор
является вектор  .
.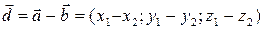 .
. .
. равна
равна  .
. , где
, где  – угол между векторами
– угол между векторами  .
. .
. .
. и
и  . Найти угол между этими векторами.
. Найти угол между этими векторами. . Следовательно,
. Следовательно,  .
. , где
, где  и
и  - вещественные числа, называются комплексными числами.
- вещественные числа, называются комплексными числами. называется мнимой единицей, числа
называется мнимой единицей, числа  – мнимыми числами. Если
– мнимыми числами. Если  , то число
, то число  , число
, число  . Число
. Число  называется сопряженным числу
называется сопряженным числу  и обозначается
и обозначается  , то есть
, то есть  .
. ,
, ,
, ,
,
 . Тогда:
. Тогда:
 определена в некоторой окрестности точки
определена в некоторой окрестности точки  , стремящемся к
, стремящемся к 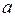 (в точке
(в точке 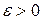 существует
существует  такое, что при
такое, что при  справедливо неравенство
справедливо неравенство  .
. .
. может и не существовать. Аналогично, запись
может и не существовать. Аналогично, запись 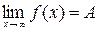 обозначает, что для любого
обозначает, что для любого  существует число
существует число  такое, что при
такое, что при  выполняется неравенство
выполняется неравенство  .
. , то
, то  .
. (или
(или  ) и
) и  (или
(или  ), то
), то , где
, где  – постоянная.
– постоянная. .
. .
. , если
, если  .
. ,
,  , где
, где  .
.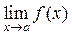 , где
, где  , начинают всегда с подстановки в
, начинают всегда с подстановки в  предельного значения её аргумента
предельного значения её аргумента  . В процессе вычисления пределов могут возникать неопределенности вида
. В процессе вычисления пределов могут возникать неопределенности вида 





 . В простейших случаях они раскрываются с помощью алгебраических преобразований.
. В простейших случаях они раскрываются с помощью алгебраических преобразований. .
. .
. при
при  , если она задана отношением двух многочленов, сначала раскладывают на множители числитель и знаменатель, а затем сокращают на
, если она задана отношением двух многочленов, сначала раскладывают на множители числитель и знаменатель, а затем сокращают на  . При этом обычно используют формулы сокращенного умножения:
. При этом обычно используют формулы сокращенного умножения:
 – корни квадратного уравнения
– корни квадратного уравнения 
 множитель выделяют разложением квадратного трёхчлена по формуле
множитель выделяют разложением квадратного трёхчлена по формуле  , где
, где  .
. множитель выделяют следующим способом:
множитель выделяют следующим способом: 
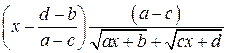
 .
. равного 3, получаем неопределенность
равного 3, получаем неопределенность  . Для разложения числителя на множители решаем квадратное уравнение
. Для разложения числителя на множители решаем квадратное уравнение  и находим корни
и находим корни  и
и  . Следовательно,
. Следовательно,  . В знаменателе выносим
. В знаменателе выносим  .После сокращения дроби на
.После сокращения дроби на  и подстановки в полученное выражение предельного значения
и подстановки в полученное выражение предельного значения  , равного 3, получим:
, равного 3, получим: .
.
 .
. . Чтобы раскрыть ее, разделим числитель и знаменатель дроби на наибольшую степень
. Чтобы раскрыть ее, разделим числитель и знаменатель дроби на наибольшую степень  . Знаменатель полученной дроби при
. Знаменатель полученной дроби при  не равен 0, следовательно, применяя теоремы о пределах получим:
не равен 0, следовательно, применяя теоремы о пределах получим:

 её предельного значения
её предельного значения  получим неопределённость
получим неопределённость  . Для её раскрытия сначала разделим числитель и знаменатель дроби на
. Для её раскрытия сначала разделим числитель и знаменатель дроби на  (старшую степень переменной
(старшую степень переменной 

 получим неопределённость
получим неопределённость  , где
, где  – некоторое число, т.е. множитель
– некоторое число, т.е. множитель  . Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
. Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.

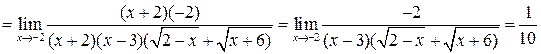 .
.

 ,
,
 ,
, ,
, .
.
 ,
,  ,
,  (
( ).
). называется непрерывной в точке
называется непрерывной в точке  , если для
, если для  справедливо неравенство
справедливо неравенство  .
. .
. в точке число
в точке число  может быть любым числом, в частности
может быть любым числом, в частности  .
. .
.
 , выяснить является ли
, выяснить является ли 


 в точке
в точке  0) также являются непрерывными в точке функциями.
0) также являются непрерывными в точке функциями.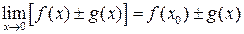

 , g (x)
, g (x)  называется непрерывной на отрезке [ а; b ] если она непрерывна в каждой точке этого отрезка.
называется непрерывной на отрезке [ а; b ] если она непрерывна в каждой точке этого отрезка.


