
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое определение вероятности события.
Геометрическое определение вероятности события. Задачи классической вероятности. Элементы комбинаторики. Комбинаторный метод вычисления вероятностей в классической схеме. Теорема умножения. Определение условной вероятности. Независимость событий. Вероятности сложных событий. Формулы умножения вероятностей. Теоремы сложения вероятностей. Формула полной вероятности, формулы Байеса. Схема независимых испытаний Бернулли. Формула Бернулли. Предельные теоремы в схеме Бернулли. Формулы Муавра-Лапласа и Пуассона. Случайные величины. Определение случайной величины. Дискретные случайные величины (ДСВ) и случайные величины непрерывного типа (СВНТ). Задание случайных величин. Закон распределения ДСВ. Числовые характеристики ДСВ. Математическое ожидание, дисперсия и другие моменты. Свойства математического ожидания и дисперсии. Примеры ДСВ. Гипергеометрическое распределение, биномиальное распределение, закон Пуассона. Задание СВНТ. Функция распределения и функция плотности вероятностей. Свойства этих функций. Числовые характеристики СВНТ. Совместное распределение нескольких случайных величин. Функции случайных величин и их числовые характеристики. Независимость случайных величин. Примеры непрерывных распределений. Равномерное, нормальное и показательное распределения. Ковариация, коэффициент корреляции. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Предельные теоремы. Понятие о предельных теоремах. Центральная предельная теорема для суммы одинаково распределенных слагаемых. Теорема Ляпунова. Математическая статистика. Выборка и способы ее представления. Числовые характеристики выборочного распределения. Точечные оценки и их свойства. Статистическое оценивание характеристик распределения генеральной совокупности по выборке. Интервальные оценки. Доверительный интервал, надежность и точность оценки. Доверительный интервал для центра нормального распределения при известной дисперсии. Доверительный интервал для среднего квадратичного отклонения нормального распределения.
Проверка статистических гипотез. Критерий согласия Пирсона. Линейная регрессия. Элементы регрессионного анализа и метод наименьших квадратов. Характер связи и его оценивание по коэффициенту корреляции. ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №4 Задача №1. Исследовать сходимость положительного ряда, применяя какой – либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный):
Задача №2. Найти интервал сходимости степенного ряда, исследовать его поведение на концах интервала сходимости и указать область сходимости:
Задача №3 (Комбинаторный метод вычисления вероятностей в классической схеме).
Варианты 1, 2 В магазин поступило n телевизоров. Из них k имеют скрытые дефекты. Покупателю для выбора наудачу предложено l телевизоров. Какова вероятность того, что все предложенные покупателю изделия не содержат дефектов? 1. n=30, k=3, l=2. 2. n=20, k=2, l=3. Варианты 3,4 Из партии, содержащей n изделий, среди которых k бракованных, наудачу извлекают m изделий для контроля. Найти вероятности следующих событий: А={в полученной выборке ровно l бракованных изделий}, B={в полученной выборке нет бракованных изделий}. 3. n=10, k=3, l=1, m=4. 4. n=12, k=3, l=2, m=5 Варианты 5,6 Имеются два ящика с деталями. В первом n деталей, из них m годных. Во втором ящике N изделий, из них M годных. Сборщик наудачу выбрал по одной детали из каждого ящика. Найти вероятность того, что обе выбранные детали годные. Какова вероятность того, что обе выбранные детали бракованные? 5. n=12, m=8, N=8, M=7. 6. n=14, m=10, N=6, M=4. Варианты 7,8 Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если: 7. число мест равно 8. 8. число мест равно 12.
Варианты 9,10 Из урны, содержащей m+n шаров, из которых m белых и n черных, на удачу отбирают k шаров и откладывают в сторону. Найти вероятности следующих событий: A={все отложенные шары белые}, B={среди отложенных шаров ровно l белых}.
9. m=10, n=6, k=5, l=3. 10. m=8, n=12, k=6, l=4. Задача № 4 (Вероятности сложных событий и применение теорем сложения и умножения)
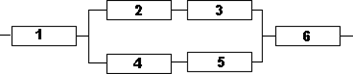
Электрическая цепь прибора составлена по схеме, приведенной на рисунке Вашего варианта. Событие Ak={k-ый элемент вышел из строя}. k=1,2,…,6. Отказы элементов являются независимыми в совокупности событиями. Известна надежность Вариант 1
Вариант 2
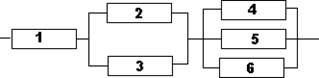
Вариант 3
Вариант 4
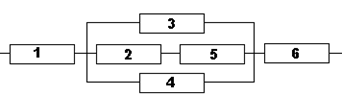
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 10
Задача № 5 (Формула полной вероятности и формула Байеса)
Варианты № 1, 2 В сборочный цех поступает некоторая деталь с трёх станков-автоматов. Среди изделий первой линии 1. 2. Варианты № 3, 4 В тире имеется три вида винтовок: 3. 4. Варианты № 5,6 В магазин поступают телевизоры с трёх заводов. С первого завода поступает 5. 6.
Варианты № 7,8 В ящике n теннисных мячей. Из них игранных m. Для первой игры наудачу взяли два мяча и после игры их положили обратно. Для второй игры также наудачу взяли два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?
7. n =10, m =2. 8. n =12, m =4.
Варианты № 9,10
Три стрелка произвели по выстрелу в одну и ту же мишень. Вероятность попадания у них соответственно р1, р2, р3. В мишени оказались две пробоины. Определите вероятность промаха n -го стрелка. 9. р1 =0.5, р2 =0.7, р3 =0.9, n =1. 10. р1 =0.6, р2 =0.8, р3 =0.9, n =2.
Задача №6 Дискретные случайные величины.
Составить закон распределения дискретной случайной величины Х. Записать функцию распределения, построить её график. Вычислить числовые характеристики М(Х), D(Х), s(Х)).
Варианты №1,2,3,4 Х -число отказавших элементов в одном опыте с устройством, состоящим из n независимо работающих элементов. Вероятность отказа каждого элемента р.
1. n = 3, p=0.1. 2. n=4, p=0.15. 3. n=3, p=0.15. 4. n=4, p=0.2.
Варианты №5,6,7 В партии k% бракованных изделий. Наудачу отобрано n изделий. Х - число бракованных изделий среди отобранных. Дискретная случайная величина Х распределена по биномиальному закону: 5. k=15%, n=4. 6. k=10%, n=5. 7. k=20%, n=3.
Варианты №8,9,10 В партии из n деталей имеется m стандартных. Наудачу отобрали k деталей. Х -число стандартных деталей среди отобранных. 8. n=10, m=8, k=3. 9. n=9, m=7, k=3. 10. n=12, m=10, k=3.
Задача № 7 (Выборка, выборочные характеристики) Из изучаемой налоговыми органами обширной группы населения случайным образом отобраны 10 человек и собраны сведения об их доходах за истекший год в тысячах рублей: х1, х2,…, х10. Найти выборочное среднее, исправленную выборочную дисперсию. Считая распределение доходов в группе нормальным и принимая в качестве его параметров выборочные характеристики, определить, какой процент населения имеет годовой доход, превышающий 70 тыс. рублей.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.244.44 (0.063 с.) |











 k-го элемента (соответственно
k-го элемента (соответственно  - вероятность отказа). Событие B={разрыв цепи}. Выразить событие B в алгебре событий Ak. Найти вероятность отказа прибора и вероятность надежности схемы. p1=p2=0.9, p3=p4=0.8, p5=p6=0.85.
- вероятность отказа). Событие B={разрыв цепи}. Выразить событие B в алгебре событий Ak. Найти вероятность отказа прибора и вероятность надежности схемы. p1=p2=0.9, p3=p4=0.8, p5=p6=0.85.






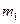 % стандартных, у второй линии
% стандартных, у второй линии  %,
%,  % - у третьей линии. Объём продукции первой линии
% - у третьей линии. Объём продукции первой линии  %, второй линии
%, второй линии  %. Определить вероятность того, что наудачу взятая сборщиком деталь окажется бракованной. Определить вероятность того, что деталь изготовлена на третьей линии, если оказалось, что она бракованная.
%. Определить вероятность того, что наудачу взятая сборщиком деталь окажется бракованной. Определить вероятность того, что деталь изготовлена на третьей линии, если оказалось, что она бракованная. -третьего типа. Вероятность попадания в цель из винтовок первого типа
-третьего типа. Вероятность попадания в цель из винтовок первого типа  , второго типа
, второго типа  , третьего типа
, третьего типа  . После выстрела из винтовки, выбранной наудачу, цель была поражена. Какова вероятность того, что выстрел был сделан из винтовки третьего типа?
. После выстрела из винтовки, выбранной наудачу, цель была поражена. Какова вероятность того, что выстрел был сделан из винтовки третьего типа?


