Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятности события.Стр 1 из 4Следующая ⇒ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Математика»
КОНТРОЛЬНАЯ РАБОТА №4 ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
Ростов-на-Дону
Составители: Волокитин Г.И., Тукодова О.М., Глушкова В.Н. Контрольная работа №4 для студентов заочной формы обучения технических специальностей – Ростов н/д: Издательский центр ДГТУ. 2013. – … с.
Для студентов заочной формы обучения технических специальностей
Печатается по решению методической комиссии факультета «Информатика и вычислительная техника»
ПРОГРАММА по высшей математике для студентов первого курса заочной формы обучения (второй семестр) Числовые ряды. Определение суммы ряда и основные свойства. Примеры геометрического и гармонического рядов. Необходимый признак сходимости. Положительные ряды. Критерий сходимости положительных рядов. Достаточные признаки сходимости: первый и второй признаки сравнения, признак Даламбера, радикальный и интегральный признаки Коши. Знакочередующиеся ряды. Понятие абсолютной и условной сходимости знакопеременных рядов. Теорема Лейбница о сходимости знакочередующихся рядов и следствие из этой теоремы об оценке остатка ряда. Степенные ряды. Теорема Абеля и следствие из этой теоремы о существовании для степенных рядов интервала сходимости. Радиус сходимости степенного ряда и его вычисление. Свойства степенных рядов: теоремы о непрерывности суммы степенного ряда, о почленном интегрировании и почленном дифференцировании. Логарифмический ряд. Ряды Тэйлора и Маклорена. Условия представимости функции ее рядом Тэйлора. Единственность представления заданной функции степенным рядом. Разложение элементарных функций ex, cos x, sin x, (1+x)m в степенные ряды. Применение степенных рядов к приближенным вычислениям. Ряды Фурье. Понятие тригонометрического ряда. Определение ортогональных систем функций и тригонометрическая система функций. Формулы Эйлера-Фурье и определение ряда Фурье. Достаточные условия представимости функции с периодом T=2p ее рядом Фурье (теорема Дирихле). Ряд Фурье для четных и нечетных функций. Периодическое продолжение функций. Ряд Фурье в случае произвольного периода T=2l и ряд Фурье для функции, заданной на несимметричном интервале. Основные понятия. Случайные события. Алгебраические операции над событиями. Множество элементарных событий. Алгебра событий. Аксиоматическое определение вероятности события. Вероятностное пространство. Классическое определение вероятности события. Статистическое определение вероятности события. Геометрическое определение вероятности события. Задачи классической вероятности. Элементы комбинаторики. Комбинаторный метод вычисления вероятностей в классической схеме. Теорема умножения. Определение условной вероятности. Независимость событий. Вероятности сложных событий. Формулы умножения вероятностей. Теоремы сложения вероятностей. Формула полной вероятности, формулы Байеса. Схема независимых испытаний Бернулли. Формула Бернулли. Предельные теоремы в схеме Бернулли. Формулы Муавра-Лапласа и Пуассона. Случайные величины. Определение случайной величины. Дискретные случайные величины (ДСВ) и случайные величины непрерывного типа (СВНТ). Задание случайных величин. Закон распределения ДСВ. Числовые характеристики ДСВ. Математическое ожидание, дисперсия и другие моменты. Свойства математического ожидания и дисперсии. Примеры ДСВ. Гипергеометрическое распределение, биномиальное распределение, закон Пуассона. Задание СВНТ. Функция распределения и функция плотности вероятностей. Свойства этих функций. Примеры непрерывных распределений. Равномерное, нормальное и показательное распределения. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Предельные теоремы. Понятие о предельных теоремах. Центральная предельная теорема для суммы одинаково распределенных слагаемых. Теорема Ляпунова. Математическая статистика. Выборка и способы ее представления. Числовые характеристики выборочного распределения. Интервальные оценки. Доверительный интервал, надежность и точность оценки. Линейная регрессия. Элементы регрессионного анализа и метод наименьших квадратов. Характер связи и его оценивание по коэффициенту корреляции. ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ №4 Задача №1. Исследовать сходимость положительного ряда, применяя какой – либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный):
Задача №2. Найти интервал сходимости степенного ряда, исследовать его поведение на концах интервала сходимости и указать область сходимости:
Задача №3 (Комбинаторный метод вычисления вероятностей в классической схеме).
Варианты 1, 2 В магазин поступило n телевизоров. Из них k имеют скрытые дефекты. Покупателю для выбора наудачу предложено l телевизоров. Какова вероятность того, что все предложенные покупателю изделия не содержат дефектов? 1. n=30, k=3, l=2. 2. n=20, k=2, l=3. Варианты 3,4 Из партии, содержащей n изделий, среди которых k бракованных, наудачу извлекают m изделий для контроля. Найти вероятности следующих событий: А={в полученной выборке ровно l бракованных изделий}, B={в полученной выборке нет бракованных изделий}. 3. n=10, k=3, l=1, m=4. 4. n=12, k=3, l=2, m=5 Варианты 5,6 Имеются два ящика с деталями. В первом n деталей, из них m годных. Во втором ящике N изделий, из них M годных. Сборщик наудачу выбрал по одной детали из каждого ящика. Найти вероятность того, что обе выбранные детали годные. Какова вероятность того, что обе выбранные детали бракованные? 5. n=12, m=8, N=8, M=7. 6. n=14, m=10, N=6, M=4. Варианты 7,8 Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если: 7. число мест равно 8. 8. число мест равно 12.
Варианты 9,10 Из урны, содержащей m+n шаров, из которых m белых и n черных, на удачу отбирают k шаров и откладывают в сторону. Найти вероятности следующих событий: A={все отложенные шары белые}, B={среди отложенных шаров ровно l белых}. 9. m=10, n=6, k=5, l=3. 10. m=8, n=12, k=6, l=4. Задача № 4 (Вероятности сложных событий и применение теорем сложения и умножения)
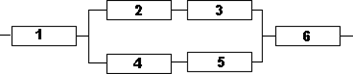
Электрическая цепь прибора составлена по схеме, приведенной на рисунке Вашего варианта. Событие Ak={k-ый элемент вышел из строя}. k=1,2,…,6. Отказы элементов являются независимыми в совокупности событиями. Известна надежность Вариант 1
Вариант 2
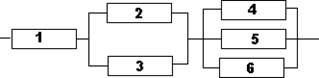
Вариант 3
Вариант 4
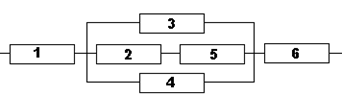
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 10
Задача № 5 (Формула полной вероятности и формула Байеса)
Варианты № 1, 2 В сборочный цех поступает некоторая деталь с трёх станков-автоматов. Среди изделий первой линии 1. 2. Варианты № 3, 4 В тире имеется три вида винтовок: 3. 4. Варианты № 5,6 В магазин поступают телевизоры с трёх заводов. С первого завода поступает 5. 6.
Варианты № 7,8 В ящике n теннисных мячей. Из них игранных m. Для первой игры наудачу взяли два мяча и после игры их положили обратно. Для второй игры также наудачу взяли два мяча. Какова вероятность того, что вторая игра будет проводиться новыми мячами?
7. n =10, m =2. 8. n =12, m =4.
Варианты № 9,10
Три стрелка произвели по выстрелу в одну и ту же мишень. Вероятность попадания у них соответственно р1, р2, р3. В мишени оказались две пробоины. Определите вероятность промаха n -го стрелка. 9. р1 =0.5, р2 =0.7, р3 =0.9, n =1. 10. р1 =0.6, р2 =0.8, р3 =0.9, n =2.
Задача №6 Дискретные случайные величины.
Составить закон распределения дискретной случайной величины Х. Записать функцию распределения, построить её график. Вычислить числовые характеристики М(Х), D(Х), s(Х)).
Варианты №1,2,3,4 Х -число отказавших элементов в одном опыте с устройством, состоящим из n независимо работающих элементов. Вероятность отказа каждого элемента р. 1. n = 3, p=0.1. 2. n=4, p=0.15. 3. n=3, p=0.15. 4. n=4, p=0.2.
Варианты №5,6,7 В партии k% бракованных изделий. Наудачу отобрано n изделий. Х - число бракованных изделий среди отобранных. Дискретная случайная величина Х распределена по биномиальному закону: 5. k=15%, n=4. 6. k=10%, n=5. 7. k=20%, n=3.
Варианты №8,9,10 В партии из n деталей имеется m стандартных. Наудачу отобрали k деталей. Х -число стандартных деталей среди отобранных. 8. n=10, m=8, k=3. 9. n=9, m=7, k=3. 10. n=12, m=10, k=3.
Задача № 7 (Выборка, выборочные характеристики) Из изучаемой налоговыми органами обширной группы населения случайным образом отобраны 10 человек и собраны сведения об их доходах за истекший год в тысячах рублей: х1, х2,…, х10. Найти выборочное среднее, исправленную выборочную дисперсию. Считая распределение доходов в группе нормальным и принимая в качестве его параметров выборочные характеристики, определить, какой процент населения имеет годовой доход, превышающий 70 тыс. рублей.
ЭЛЕМЕНТЫ ТЕОРИИ РЯДОВ
Положительные ряды. Для исследования сходимости положительных рядов (т.е. рядов с неотрицательными членами: un ³0) применяют достаточные признаки сходимости рядов. Среди них наиболее часто используют признаки сравнения, Даламбера, радикальный и интегральный признаки Коши
(Табл. 1). Пример 2. Исследовать сходимость ряда
Решение. Применим первый признак сравнения. В качестве «эталонного» ряда возьмем обобщенный гармонический ряд
Показатель степени гармонического ряда p =4/5<1, поэтому «эталонный» ряд расходящийся. Члены исходного ряда для всех n³3 превосходят соответствующие члены «эталонного» ряда: Применяя первый признак сравнения, получаем, поскольку расходится «меньший» эталонный ряд, то расходится и «больший» исходный ряд. Пример 3. Исследовать сходимость ряда
Решение. Преобразуем общий член исходного ряда Исходный ряд сравним с “эталонным” рядом
Это “геометрический ряд, он сходится, т.к. знаменатель прогрессии q =2/3<1. Поскольку
конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится. Пример 4. Исследовать сходимость ряда
Решение. Применим признак Даламбера. Записываем n- ый член ряда:  . .
(n +1 )- ый член получим, если в выражении un везде n заменим на (n+1):
Найдем предел отношения:
Следовательно, ряд сходится. Подчеркнем, здесь использовали известный «второй замечательный» предел
Пример 6. Исследовать сходимость ряда
Решение. Рассмотрим функцию Она при x³2 положительная, непрерывная и монотонно убывает. (Заметим, что эта функция получается из выражения общего члена ряда при замене n на x). Можно применять интегральный признак. Исследуем сходимость несобственного интеграла:
Из интегрального признака заключаем, поскольку несобственный интеграл сходится, то сходится и исследуемый ряд.
Знакочередующиеся ряды. Ряд, составленный из положительных и отрицательных членов (знакопеременный ряд) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из модулей его членов, расходится, тогда знакопеременный ряд называется условно (неабсолютно) сходящимся. Рассмотрим далее числовые ряды, любые два соседние члены которых имеют противоположные знаки (знакочередующиеся ряды):
Исследование сходимости знакочередующихся рядов можно начинать с проверки абсолютной сходимости. Если ряд, составленный из абсолютных величин, сходится, то и сам знакопеременный ряд сходится. Если же окажется, что данный знакочередующийся ряд не обладает абсолютной сходимостью, то исследование продолжают с помощью признака Лейбница: Теорема Лейбница. Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю при n ®¥, то ряд сходится. Его сумма имеет знак первого члена, абсолютное значение этой суммы не превышает абсолютное значение первого из членов.
Важное значение имеет следствие из теоремы Лейбница: для сходящегося знакочередующегося ряда абсолютная ошибка приближенного равенства S @ Sn (абсолютная величина остатка ряда) не превосходит модуль первого из отброшенных членов: Пример 7. Исследовать сходимость ряда
Решение. Данный ряд знакочередующийся, т.к.
Исходный ряд можно переписать в виде Рассмотрим сначала ряд, составленный из абсолютных величин исходного ряда:
Сравним его с гармоническим рядом 1+1/2+1/3+…+1/ n +…, о котором известно, что он расходится. Так как то по второму признаку сравнения заключаем, что ряд из модулей расходится и, следовательно, исходный ряд абсолютно не сходится. Продолжим исследование с помощью признака Лейбница: члены исходного ряда удовлетворяют условиям 1) монотонного убывания абсолютных величин членов ряда; 2) общий член ряда стремится к нулю. В самом деле, в промежутке [0, p/2] функция y = tg x монотонно возрастает, а при n = 1, 2, … выполняются неравенства
Окончательно заключаем, исходный ряд сходится условно. Степенные ряды.
Степенным рядом называется функциональный ряд вида: где множители при степенях (x – x0) – коэффициенты ряда, число x0 – центр интервала сходимости. При частном значении переменной x степенной ряд становится числовым. Сходимость степенного ряда зависит от величины x. Из теоремы Абеля для степенных рядов следует, что область сходимости всякого степенного ряда – некоторый интервал (x0–R, x0+R), называемый интервалом сходимости. Во всех точках этого интервала степенной ряд сходится и притом абсолютно, вне интервала – ряд расходится. На границе интервала различные степенные ряды ведут себя по-разному. Число R – половина длины интервала сходимости – радиус сходимости. Если степенной ряд сходится лишь в одной точке, то радиус R = 0. Если ряд сходится при любом x, то R = ¥.Радиус сходимости степенного ряда можно найти по формуле:
если соответствующие пределы существуют – конечные или бесконечные. При этом R = 0, если L = 0 и R = ¥, если L = 0. Пример 8. Найти область сходимости степенного ряда
Решение. В развернутом виде ряд выглядит следующим образом
Коэффициенты ряда:
Найдем радиус сходимости
Заключаем, что интервал сходимости (-1/3, 1/3). Исследуем далее сходимость степенного ряда в граничных точках интервала:
а) при x= 1/3 получим числовой положительный ряд: Этот ряд расходится, что видно из сравнения его с гармоническим рядом.
б) при x = -1/3 получим знакочередующийся ряд: Члены этого ряда удовлетворяют условиям теоремы Лейбница:
Знакочередующийся ряд сходится, т.е. при X = -1/3 степенной ряд сходится и окончательно область сходимости степенного ряда определяется неравенствами –1/3 £ X < 1/3. При решении примеров на применение степенных разложений к приближенным вычислениям (задача5) следует использовать известные формулы разложения элементарных функций в ряды Маклорена. Они помещены в таблице 2. Заметим, что важную роль здесь выполняет следствие из теоремы Лейбница: для сходящегося знакочередующегося ряда остаток по абсолютной величине не превосходит первого из отброшенных членов. Опираясь на это следствие легко установить, сколько членов ряда нужно просуммировать, чтобы получить результат с заданной точностью. Разумеется, все расчеты надо проводить в рамках этой точности. Пример 9. С точностью до e = 0.0001 вычислить exp (-0.1). Решение. Используем разложение (табл. 2)
Полагая x= -0.1, имеем
Получили знакочередующийся ряд. Величина его остатка по абсолютной величине не превосходит первого из отброшенных членов. Возьмем 4 члена ряда, тогда погрешность не превышает величины 0.0000042, т.е.
Каждое из оставленных четырех слагаемых учитываем, удерживая 5 цифр после запятой. При этом, округляя, в ответе будем иметь 4 верных десятичных знака: exp (-0.1)= 0.9048. Пример 10. С точностью до e = 0.0001 вычислить интеграл
Решение. Интеграл вычислим, разлагая подынтегральную функцию в степенной ряд. При этом воспользуемся формулой (табл. 2):
Имеем
Степенной ряд можно почленно интегрировать и почленно дифференцировать любое число раз, при этом радиус сходимости не меняется (основное свойство степенных рядов). Выполняя почленно интегрирование, имеем
Получился знакочередующийся ряд, причем | R 3| < 1/15120 @0.00007 < e. Поэтому с заданной точностью имеем
Ряды Фурье. Функциональный ряд вида
где l >0, an, bn – постоянные, называется тригонометрическим рядом. Все члены тригонометрического ряда и его сумма, если она существует, являются периодическими функциями от x с периодом T=2 l. Рядом Фурье для функции f(x) в интервале (-l, l) называется тригонометрический ряд, у которого коэффициенты an, bn вычисляются по формулам Эйлера-Фурье:
Обозначают
Достаточные условия, при выполнении которых данную функцию f(x) можно разложить в ряд Фурье, сформулированы в следующей теореме. Т еорема Дирихле: если в интервале (-l, l) функция f(x), для которой существуют предельные значения f(-l+0) и f(l-0), непрерывна всюду, кроме, быть может, конечного числа точек разрыва первого рода, и имеет конечное число точек экстремума (либо не имеет их совсем), то соответствующий ей ряд Фурье сходится. Сумма этого ряда равна 1) f(x) в тех точках х интервала, в которых функция непрерывна; 2) полусумме односторонних пределов функции слева и справа ½[f(xk-0)+f(xk+0)] во всех точках разрыва xk; 3) ½[f(-l+0)+f(l-0)] на концах интервала. Для четной функции все коэффициенты bn = 0 и соответствующий ряд Фурье не содержит синусов:
Для нечетной функции f(x) все коэффициенты an = 0 и соответствующий ряд Фурье содержит только синусы:
Функцию f(x), заданную в промежутке (0, l) можно произвольно продолжить в интервал (-l, 0) и поэтому она представима различными рядами Фурье. Так, при четном доопределении f(x) в интервале (-l, 0), получаем ряд по косинусам, при нечетном – ряд по синусам. Однако, все эти ряды на основном интервале (0, l) сходятся именно к f(x) (разумеется, при выполнении условий представления функции ее рядом Фурье). Если в интервале задания (0, l) функция f(x) непрерывна, то при четном ее продолжении кривая, представляющая 2 l – периодическую функцию, не имеет разрывов. При разложении в ряд Фурье функция f(x) может быть задана на произвольном (не обязательно симметричном) интервале (a, a+2l). В этом случае коэффициенты an, bn вычисляются по формулам с другими пределами интегрирования:
Если функция f(x) определена несколькими различными формулами на разных участках интервала, то при вычислении коэффициентов ряда Фурье учитывается свойство аддитивности определенного интеграла. Пример 11. Функция f(x) определена в интервале (0, π) графиком
y
π/2 π
Найти выражение заданной функции в виде ряда Фурье по косинусам. Решение. 1) Составим аналитическое выражение функции f(x) на отрезке (0, π): 1)
Так как требуется разложить f(x) в ряд по косинусам, то в соседний интервал (- π, 0) ее продолжим четным образом. Полупериод в данном случае определяется величиной l = π. Ряд Фурье приобретает вид:
График функции f(x) c ее четным продолжением в интервал (- π, 0) последующим 2π – периодическим продолжением выглядит следующим образом:
y
-2π -3/2π -π -π/2 0 π/2 π 3/2π 2π
2) Вычислим коэффициенты ряда Фурье:
Остальные коэффициенты найдем, интегрируя по частям первый из интегралов:
4) Поскольку функция f(x) удовлетворяет всем трем условиям теоремы Дирихле, то она представима рядом Фурье. В силу непрерывности периодического продолжения f(x) ряд Фурье сходится к самой функции f(x) в каждой точке x. Используя найденные значения коэффициентов ряда, получим искомое разложение:
5) Поскольку функция, получившаяся при четном продолжении f(x) в точке х = 0 непрерывна, то сумма ряда Фурье принимает значени
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.212.145 (0.006 с.) |











 k-го элемента (соответственно
k-го элемента (соответственно  - вероятность отказа). Событие B={разрыв цепи}. Выразить событие B в алгебре событий Ak. Найти вероятность отказа прибора и вероятность надежности схемы. p1=p2=0.9, p3=p4=0.8, p5=p6=0.85.
- вероятность отказа). Событие B={разрыв цепи}. Выразить событие B в алгебре событий Ak. Найти вероятность отказа прибора и вероятность надежности схемы. p1=p2=0.9, p3=p4=0.8, p5=p6=0.85.






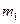 % стандартных, у второй линии
% стандартных, у второй линии  %,
%,  % - у третьей линии. Объём продукции первой линии
% - у третьей линии. Объём продукции первой линии  %, второй линии
%, второй линии  %. Определить вероятность того, что наудачу взятая сборщиком деталь окажется бракованной. Определить вероятность того, что деталь изготовлена на третьей линии, если оказалось, что она бракованная.
%. Определить вероятность того, что наудачу взятая сборщиком деталь окажется бракованной. Определить вероятность того, что деталь изготовлена на третьей линии, если оказалось, что она бракованная. -третьего типа. Вероятность попадания в цель из винтовок первого типа
-третьего типа. Вероятность попадания в цель из винтовок первого типа  , второго типа
, второго типа  , третьего типа
, третьего типа  . После выстрела из винтовки, выбранной наудачу, цель была поражена. Какова вероятность того, что выстрел был сделан из винтовки третьего типа?
. После выстрела из винтовки, выбранной наудачу, цель была поражена. Какова вероятность того, что выстрел был сделан из винтовки третьего типа?






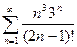





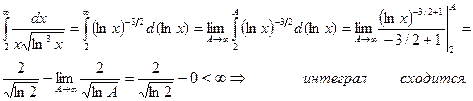


























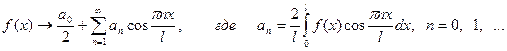







 π/2
π/2 x
x










 π/2 - - - - - - - ------ - - - -
π/2 - - - - - - - ------ - - - -