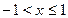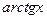Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие теоретические сведения и образцы решений задач
ЭЛЕМЕНТЫ ТЕОРИИ РЯДОВ
Понятие числового ряда. Необходимый признак сходимости. Определение. Бесконечная сумма членов числовой последовательности { un } называется числовым рядом:
Здесь un (n=1, 2, 3, …) – n-ый член ряда. Сумма конечного числа n первых членов ряда Если существует конечный предел последовательности { Sn } частичных сумм то этот предел называется суммой ряда, а сам ряд называется сходящимся. Если конечный предел частичных сумм не существует, то ряд называется расходящимся. Необходимый признак сходимости ряда: если ряд Ряд может сходиться лишь в том случае, когда его общий член un при n®¥ является бесконечно малой величиной. Если необходимое условие сходимости ряда не выполнено: lim un ¹ 0, либо предел не n®¥ существует, то ряд расходится (достаточный признак расходимости рядов).
Пример 1. Найти общий член ряда Доказать,что этот ряд расходится. Решение. Последовательно рассмотрим члены ряда:
Подмечая закономерность, можно видеть, что общий член ряда выражается формулой
Представим общий член ряда в виде Ясно, что при n³4 | u n| > 3/25, поскольку все сомножители-дроби, кроме первых трех, больше 1. Отсюда следует
Положительные ряды. Для исследования сходимости положительных рядов (т.е. рядов с неотрицательными членами: un ³0) применяют достаточные признаки сходимости рядов. Среди них наиболее часто используют признаки сравнения, Даламбера, радикальный и интегральный признаки Коши
(Табл. 1). Пример 2. Исследовать сходимость ряда
Решение. Применим первый признак сравнения. В качестве «эталонного» ряда возьмем обобщенный гармонический ряд
Показатель степени гармонического ряда p =4/5<1, поэтому «эталонный» ряд расходящийся. Члены исходного ряда для всех n³3 превосходят соответствующие члены «эталонного» ряда: Применяя первый признак сравнения, получаем, поскольку расходится «меньший» эталонный ряд, то расходится и «больший» исходный ряд. Пример 3. Исследовать сходимость ряда
Решение. Преобразуем общий член исходного ряда Исходный ряд сравним с “эталонным” рядом
Это “геометрический ряд, он сходится, т.к. знаменатель прогрессии q =2/3<1. Поскольку
конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится. Пример 4. Исследовать сходимость ряда
Решение. Применим признак Даламбера. Записываем n- ый член ряда:  . .
(n +1 )- ый член получим, если в выражении un везде n заменим на (n+1):
Найдем предел отношения:
Следовательно, ряд сходится. Подчеркнем, здесь использовали известный «второй замечательный» предел
Пример 6. Исследовать сходимость ряда
Решение. Рассмотрим функцию Она при x³2 положительная, непрерывная и монотонно убывает. (Заметим, что эта функция получается из выражения общего члена ряда при замене n на x). Можно применять интегральный признак. Исследуем сходимость несобственного интеграла:
Из интегрального признака заключаем, поскольку несобственный интеграл сходится, то сходится и исследуемый ряд.
Знакочередующиеся ряды. Ряд, составленный из положительных и отрицательных членов (знакопеременный ряд) называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из модулей его членов, расходится, тогда знакопеременный ряд называется условно (неабсолютно) сходящимся. Рассмотрим далее числовые ряды, любые два соседние члены которых имеют противоположные знаки (знакочередующиеся ряды):
Исследование сходимости знакочередующихся рядов можно начинать с проверки абсолютной сходимости. Если ряд, составленный из абсолютных величин, сходится, то и сам знакопеременный ряд сходится. Если же окажется, что данный знакочередующийся ряд не обладает абсолютной сходимостью, то исследование продолжают с помощью признака Лейбница:
Теорема Лейбница. Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю при n ®¥, то ряд сходится. Его сумма имеет знак первого члена, абсолютное значение этой суммы не превышает абсолютное значение первого из членов.
Важное значение имеет следствие из теоремы Лейбница: для сходящегося знакочередующегося ряда абсолютная ошибка приближенного равенства S @ Sn (абсолютная величина остатка ряда) не превосходит модуль первого из отброшенных членов: Пример 7. Исследовать сходимость ряда
Решение. Данный ряд знакочередующийся, т.к.
Исходный ряд можно переписать в виде Рассмотрим сначала ряд, составленный из абсолютных величин исходного ряда:
Сравним его с гармоническим рядом 1+1/2+1/3+…+1/ n +…, о котором известно, что он расходится. Так как то по второму признаку сравнения заключаем, что ряд из модулей расходится и, следовательно, исходный ряд абсолютно не сходится. Продолжим исследование с помощью признака Лейбница: члены исходного ряда удовлетворяют условиям 1) монотонного убывания абсолютных величин членов ряда; 2) общий член ряда стремится к нулю. В самом деле, в промежутке [0, p/2] функция y = tg x монотонно возрастает, а при n = 1, 2, … выполняются неравенства
Окончательно заключаем, исходный ряд сходится условно. Степенные ряды.
Степенным рядом называется функциональный ряд вида: где множители при степенях (x – x0) – коэффициенты ряда, число x0 – центр интервала сходимости. При частном значении переменной x степенной ряд становится числовым. Сходимость степенного ряда зависит от величины x. Из теоремы Абеля для степенных рядов следует, что область сходимости всякого степенного ряда – некоторый интервал (x0–R, x0+R), называемый интервалом сходимости. Во всех точках этого интервала степенной ряд сходится и притом абсолютно, вне интервала – ряд расходится. На границе интервала различные степенные ряды ведут себя по-разному. Число R – половина длины интервала сходимости – радиус сходимости. Если степенной ряд сходится лишь в одной точке, то радиус R = 0. Если ряд сходится при любом x, то R = ¥.Радиус сходимости степенного ряда можно найти по формуле:
если соответствующие пределы существуют – конечные или бесконечные. При этом R = 0, если L = 0 и R = ¥, если L = 0. Пример 8. Найти область сходимости степенного ряда
Решение. В развернутом виде ряд выглядит следующим образом
Коэффициенты ряда:
Найдем радиус сходимости
Заключаем, что интервал сходимости (-1/3, 1/3). Исследуем далее сходимость степенного ряда в граничных точках интервала:
а) при x= 1/3 получим числовой положительный ряд: Этот ряд расходится, что видно из сравнения его с гармоническим рядом.
б) при x = -1/3 получим знакочередующийся ряд: Члены этого ряда удовлетворяют условиям теоремы Лейбница:
Знакочередующийся ряд сходится, т.е. при X = -1/3 степенной ряд сходится и окончательно область сходимости степенного ряда определяется неравенствами –1/3 £ X < 1/3. При решении примеров на применение степенных разложений к приближенным вычислениям (задача5) следует использовать известные формулы разложения элементарных функций в ряды Маклорена. Они помещены в таблице 2. Заметим, что важную роль здесь выполняет следствие из теоремы Лейбница: для сходящегося знакочередующегося ряда остаток по абсолютной величине не превосходит первого из отброшенных членов. Опираясь на это следствие легко установить, сколько членов ряда нужно просуммировать, чтобы получить результат с заданной точностью. Разумеется, все расчеты надо проводить в рамках этой точности.
Пример 9. С точностью до e = 0.0001 вычислить exp (-0.1). Решение. Используем разложение (табл. 2)
Полагая x= -0.1, имеем
Получили знакочередующийся ряд. Величина его остатка по абсолютной величине не превосходит первого из отброшенных членов. Возьмем 4 члена ряда, тогда погрешность не превышает величины 0.0000042, т.е.
Каждое из оставленных четырех слагаемых учитываем, удерживая 5 цифр после запятой. При этом, округляя, в ответе будем иметь 4 верных десятичных знака: exp (-0.1)= 0.9048. Пример 10. С точностью до e = 0.0001 вычислить интеграл
Решение. Интеграл вычислим, разлагая подынтегральную функцию в степенной ряд. При этом воспользуемся формулой (табл. 2):
Имеем
Степенной ряд можно почленно интегрировать и почленно дифференцировать любое число раз, при этом радиус сходимости не меняется (основное свойство степенных рядов). Выполняя почленно интегрирование, имеем
Получился знакочередующийся ряд, причем | R 3| < 1/15120 @0.00007 < e. Поэтому с заданной точностью имеем
Ряды Фурье. Функциональный ряд вида
где l >0, an, bn – постоянные, называется тригонометрическим рядом. Все члены тригонометрического ряда и его сумма, если она существует, являются периодическими функциями от x с периодом T=2 l. Рядом Фурье для функции f(x) в интервале (-l, l) называется тригонометрический ряд, у которого коэффициенты an, bn вычисляются по формулам Эйлера-Фурье:
Обозначают
Достаточные условия, при выполнении которых данную функцию f(x) можно разложить в ряд Фурье, сформулированы в следующей теореме. Т еорема Дирихле: если в интервале (-l, l) функция f(x), для которой существуют предельные значения f(-l+0) и f(l-0), непрерывна всюду, кроме, быть может, конечного числа точек разрыва первого рода, и имеет конечное число точек экстремума (либо не имеет их совсем), то соответствующий ей ряд Фурье сходится. Сумма этого ряда равна 1) f(x) в тех точках х интервала, в которых функция непрерывна; 2) полусумме односторонних пределов функции слева и справа ½[f(xk-0)+f(xk+0)] во всех точках разрыва xk; 3) ½[f(-l+0)+f(l-0)] на концах интервала.
Для четной функции все коэффициенты bn = 0 и соответствующий ряд Фурье не содержит синусов:
Для нечетной функции f(x) все коэффициенты an = 0 и соответствующий ряд Фурье содержит только синусы:
Функцию f(x), заданную в промежутке (0, l) можно произвольно продолжить в интервал (-l, 0) и поэтому она представима различными рядами Фурье. Так, при четном доопределении f(x) в интервале (-l, 0), получаем ряд по косинусам, при нечетном – ряд по синусам. Однако, все эти ряды на основном интервале (0, l) сходятся именно к f(x) (разумеется, при выполнении условий представления функции ее рядом Фурье). Если в интервале задания (0, l) функция f(x) непрерывна, то при четном ее продолжении кривая, представляющая 2 l – периодическую функцию, не имеет разрывов. При разложении в ряд Фурье функция f(x) может быть задана на произвольном (не обязательно симметричном) интервале (a, a+2l). В этом случае коэффициенты an, bn вычисляются по формулам с другими пределами интегрирования:
Если функция f(x) определена несколькими различными формулами на разных участках интервала, то при вычислении коэффициентов ряда Фурье учитывается свойство аддитивности определенного интеграла. Пример 11. Функция f(x) определена в интервале (0, π) графиком
y
π/2 π
Найти выражение заданной функции в виде ряда Фурье по косинусам. Решение. 1) Составим аналитическое выражение функции f(x) на отрезке (0, π): 1)
Так как требуется разложить f(x) в ряд по косинусам, то в соседний интервал (- π, 0) ее продолжим четным образом. Полупериод в данном случае определяется величиной l = π. Ряд Фурье приобретает вид:
График функции f(x) c ее четным продолжением в интервал (- π, 0) последующим 2π – периодическим продолжением выглядит следующим образом:
y
-2π -3/2π -π -π/2 0 π/2 π 3/2π 2π
2) Вычислим коэффициенты ряда Фурье:
Остальные коэффициенты найдем, интегрируя по частям первый из интегралов:
4) Поскольку функция f(x) удовлетворяет всем трем условиям теоремы Дирихле, то она представима рядом Фурье. В силу непрерывности периодического продолжения f(x) ряд Фурье сходится к самой функции f(x) в каждой точке x. Используя найденные значения коэффициентов ряда, получим искомое разложение:
5) Поскольку функция, получившаяся при четном продолжении f(x) в точке х = 0 непрерывна, то сумма ряда Фурье принимает значение 0. Ниже в таблицах 1 и 2 помещены некоторые справочные сведения, необходимые при решении задач контрольной работы №9.
Примечание. Из трех признаков (Даламбера, радикальный и интегральный) наиболее сильным является интегральный признак. Возможности радикального признака и признака Даламбера примерно равны.
Таблица 1. Достаточные признаки сходимости положительных рядов
Таблица 2. Разложения элементарных функций в степенные ряды
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.154.103 (0.083 с.) |

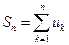 называется n-ой частичной суммой ряда.
называется n-ой частичной суммой ряда. ,
,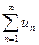 сходится, то общий член ряда стремится к нулю:
сходится, то общий член ряда стремится к нулю:  .
.



 ,необходимое условие сходимости не выполнено, ряд расходится.
,необходимое условие сходимости не выполнено, ряд расходится.






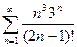





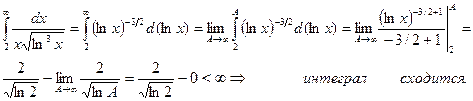


























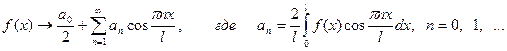







 π/2
π/2 x
x










 π/2 - - - - - - - ------ - - - -
π/2 - - - - - - - ------ - - - -




 то ряды
S un, S vn
одновременно сходятся, либо расходятся.
то ряды
S un, S vn
одновременно сходятся, либо расходятся.
 тогда при D <1 ряд сходится, а при D >1 - расходится.
тогда при D <1 ряд сходится, а при D >1 - расходится.
 то при K <1 ряд сходится, а при K >1 – расходится.
то при K <1 ряд сходится, а при K >1 – расходится.
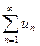 являются значениями этой функции натурального аргумента: un=f(n). Тогда ряд сходится, если сходится несобственный интеграл
являются значениями этой функции натурального аргумента: un=f(n). Тогда ряд сходится, если сходится несобственный интеграл
 Если интеграл расходится, то и ряд расходится.
Если интеграл расходится, то и ряд расходится.