
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение конструктивных параметров крепиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Прочностной расчет крепи выполняют по условию, чтобы напряжения в элементах крепи на превышали расчетного сопротивления материала.
где: Fпр – площадь поперечного сечения рассчитываемого элемента; Wпр – момент сопротивления рассчитываемого элемента в рассматриваемом сечении; Rр – расчетное сопротивление материала.
При расчете крепи удобно вначале принять Rизг и размеры сечения элемента (для дерева F = 0,785d2 и W = 0,1d3, для металла – номер профиля, F и W из справочных таблиц, а затем найти плотность расстановки рам. Плотность расстановки рам (шт/м):
При этом расчетный шаг расстановки рам составит, м
Рис П1.2. Эпюры изгибающих моментов (а), продольных сил (б). Следует затем определить Средние стойки работают только на продольное сжатие. Плотность и шаг их расстановки составляет соответственно
Шаг средних стоек принимают кратным шагу рам. Прогон под верхняками, как правило, устанавливают по технологическим соображениям с отставанием от забоя и принимают его длину 3-5 м, кратно шагу нескольких рам. Расчетная схема прогона (рис. П1.3) обычно, представляет собой многопролетную балку, нагруженную сверху сосредоточенными силами от верхняков рам.
Для прочностного расчета прогона определяют величину максимального изгибающего момента Мпр (табл. П1.1) и потребный момент сопротивления
а по его величине находят необходимый номер прокатного профиля или диаметр прогона из дерева
Затем следует проверить прочность прогона на смятие в точке контакта со средней стойкой:
где: РВ – нагрузка на прогон от одного верхняка; Fc – площадь поперечного сечения стойки; Sc и Sp – шаг средних стоек и рам, соответственно; Rсм – сопротивление смятию поперек волокон [7, 13]. Таблица П1.1 Величины максимальных изгибающих моментов в прогоне и эпюры их изменения.
Рис. П1.3 Расчетная схема прогона на стойках под верхняками. По результатам расчета нужно начертить в наглядном масштабе поперечное сечение, фрагмент продольного разреза выработки, узел соединения верхняка и стойки рамы, нижнюю часть стойки. Приложение 2 Методика расчета усилий в элементах арочной двух- и трехшарнирной крепи (рис. 2, б, г).
Арочная жесткая и податливая крепи обычно рассматриваются как двухшарнирная арка (рис. 2, б), являющаяся один раз статически неопределимой системой. В общем случае прямолинейные участки стоек имеют наклон α к горизонтальной плоскости. Реакции в опорных шарнирах: вертикальная
горизонтальная (неизвестная)
где: p – величина распределенной нагрузки; Х1 – перемещение нижнего шарнира от единичной нагрузки, м. Для определения неизвестной величины распора НХ воспользуемся методикой В.В.Смирнякова [13] (допустимо использование и других методик расчета двухшарнирных арок).
где:
Изгибающий момент М и продольная сила N в разных сечениях: прямолинейного участка DA
криволинейного участка АВ
где: для криволинейного участка Сечения с экстремальными напряжениями на криволинейном участке имеют место при
Опасное сечение на прямой части стойки находится из условия
Поперечная сила на участках DA и АВ в произвольных сечениях:
Для построения эпюр изгибающих моментов и продольных сил следует задать не меньше 6-8 точек на длине полуарки и вычислить для них M, N и Q, сведя вычисления в таблицу. При арочной крепи с вертикальными стойками (α = 90°) формулы существенно упрощаются. Арочная трехшарнирная крепь (рис. 2, г) – система статически определимая. Реакции в опорных шарнирах: вертикальная RB – см. формулу (П2.1); горизонтальная
Усилие в ключевом шарнире В
Изгибающий момент, продольная и поперечная силы в любой точке полуарки определяются, как и в двухшарнирной арке, для прямолинейного участка DA по формулам (П2.9), (П2.10) и (П2.15), а для криволинейного участка по формулам (П2.11), (П2.12) и (П2.16), в которую вместо Х1 следует подставлять значение Н/р из формулы (П2.17). Результаты расчета следует представить в виде эпюр M, N и Q.
По полученным усилиям и моментам в элементах конструкции, проводиться проверка их по несущей способности.
где: Fпр – площадь поперечного сечения рассчитываемого элемента; Wпр – момент сопротивления рассчитываемого элемента в рассматриваемом сечении; Rр – расчетное сопротивление стали. Приложение 3
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.203.255 (0.01 с.) |

 . (П2.13)
. (П2.13) . (П2.14)
. (П2.14) . (П2.15)
. (П2.15)
 по прочности боковых стоек и если она будет отличаться от
по прочности боковых стоек и если она будет отличаться от  , больше, чем на 10%, рационально изменить диаметр стоек в меньшую или большую сторону и проверить результат по формулам (П1.14) или (П1.15). Шаг рам округляют в меньшую сторону с кратностью 5 или 10 см.
, больше, чем на 10%, рационально изменить диаметр стоек в меньшую или большую сторону и проверить результат по формулам (П1.14) или (П1.15). Шаг рам округляют в меньшую сторону с кратностью 5 или 10 см. (П1.16)
(П1.16) . (П1.18)
. (П1.18) , (П1.19)
, (П1.19) . (П1.20)
. (П1.20)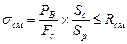 , (П1.21)
, (П1.21)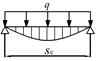


















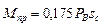





 ; (П2.1)
; (П2.1) , (П2.2)
, (П2.2) , (П2.3)
, (П2.3) , (П2.4)
, (П2.4) ,(П2.5)
,(П2.5)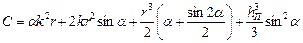 , (П2.6)
, (П2.6) ; (П2.7)
; (П2.7)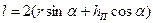 . (П2.8)
. (П2.8) ; (П2.9)
; (П2.9)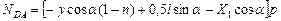 ; (П2.10)
; (П2.10) ; (П2.11)
; (П2.11) , (П2.12)
, (П2.12) , а для прямолинейного
, а для прямолинейного  .
. (ключевое сечение) и при
(ключевое сечение) и при . (П2.13)
. (П2.13) , откуда
, откуда . (П2.14)
. (П2.14) ; (П2.15)
; (П2.15) . (П2.16)
. (П2.16)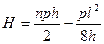 . (П2.17)
. (П2.17) . (П2.18)
. (П2.18)


