Особенности расчета траекторий инструмента

Расчет траектории инструмента при ручном программировании состоит прежде всего в определении координат опорных точек на контуре детали и на эквидистанте. При этом предполагается (см. рис. 5.1), что принятую траекторию, фиксированную опорными точками, при обработке последовательно обходит центр инструмента. При расчете траектории инструмента уточняют параметры резания на отдельных участках траектории.

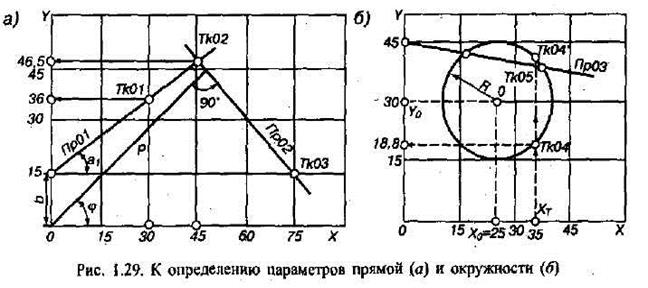
^ Расчет координат опорных точек на контуре детали. Начальный этап расчета — это определение координат опорных точек контура детали в выбранной системе координат. Для этого используют заданные на чертеже деталей размеры. Координаты опорных точек контура детали вычисляют с помощью уравнений, описывающих геометрические элементы контура детали. Точность вычислений обычно ограничивается дискретностью задания перемещений, определяемой конкретной схемой УЧПУ и используемым станком.

Наиболее часто в процессе программирования контурной обработки решаются задачи определения координат опорных точек, лежащих на прямых, окружностях и пересечениях этих элементов.

^ Прямые линии описываются уравнением у = kx b, представление которого зависит от исходных данных, В уравнении прямой к — угловой коэффициент, равный тангенсу угла наклона прямой к оси абсцисс; b — начальная ордината, равная ординате точки пересечения прямой с осью ординат (рис. 5.1).

Пользуясь этим уравнением, нетрудно для любой точки прямой определить одну координату по заданной другой.

Уравнение прямой можно составить и по другим данным:

— по известным координатам одной точки и углу наклона прямой

 

• 
  по известным координатамдвух заданных точек

Рис. 5.1. К определению параметров прямой (а) и окружности (б)

Уравнение окружности радиусом R с центром О (координаты х_0,у₀) имеет вид

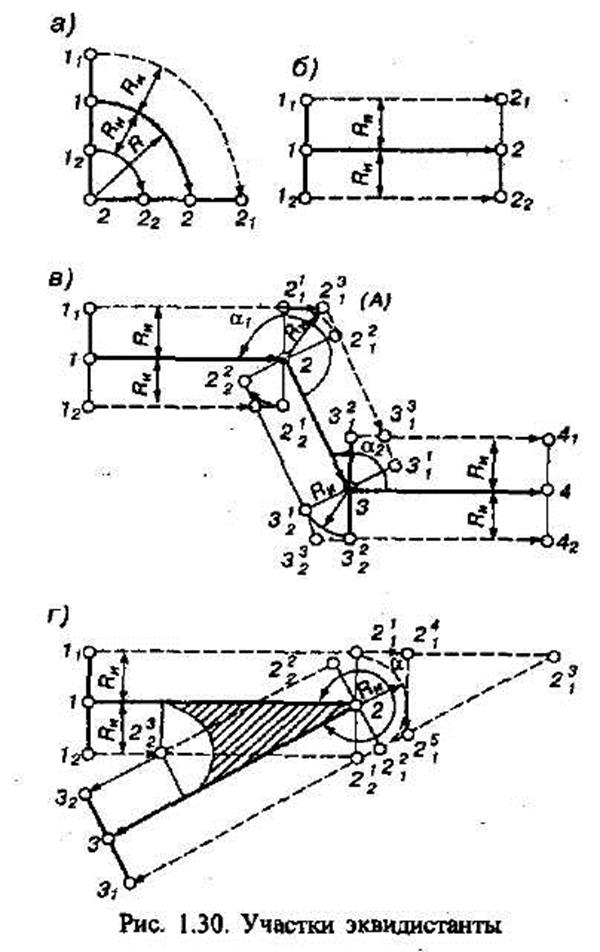
Используя уравнения прямых и окружностей достаточно просто совместным их решением определять координаты точек их пересечения или касания.

^ Расчет координат опорных точек на эквнднстанте. Координаты опорных точек эквидистантной траектории инструмента наиболее просто представить как приращение координат опорных точек контура детали. Целесообразность предварительного определения опорных точек контура очевидна, поскольку в плоскости обработки в большинстве случаев траектория центра инструмента представляет собой линию, эквидистантную обрабатываемому контуру.

Эквидистанта как геометрическое место точек, равноудаленных от контура детали на расстояние, равное радиусу R_и инструмента, строится справа или слева от элементов этого контура в зависимости от расположения инструмента относительно обрабатываемого контура. Эквидистантной к дуге окружности 1—2 является дуга концентричной ей окружности l₁ - 2₁ или l₂-2₂ с тем же центральным углом (рис. 5.2, а), а к отрезку прямой l - 2 — отрезки, параллельные данному (рис. 5.2, б).

Метод соединения элементов эквидистанты выбирают в зависимости от угла а, образованного соседними элементами контура, если смотреть со стороны расположения инструмента при обходе этого контура (рис.5.2, в). Этот угол для пары отрезков измеряют непосредственно между ними. Если же элементом контура является дуга окружности, то угол а измеряют относительно касательной к этой дуге в общей точке рассматриваемой пары элементов контура детали. Так, при a > 180° элементы эквидистанты соединяются сопрягающими дугами окружностей радиусом R_И центры которых находятся в общих точках элементов контура. При a < 180° общей точкой элементов эквидистанты является точка пересечения этих элементов (рис. 5.2). Для сопряженных элементов контура
(a =180°) элементы зквидистанты также сопряжены.

Движение центра инструмента вдоль сопрягающей дуги окружности эквидистанты при обработке острого угла контура может привести к «зарезан» из-за изменения величин и направлении сил резания. В этом случае более технологичной является траектория центра инструмента, в которой дуги сопрягающих окружностей заменены отрезками прямых, продолжающих участки эквидистанты к элементам контура.

При обходе углов a > 300° во избежание значительных отклонений траектории инструмента от эквидистанты необходимо сделать дополнительные построения. Обход острого угла (см. рис. 5.2, г) целесообразно исполнять не по дуге окружности, а продлением верхней линии эквидистанты до пересечения с нижней линией.

При вычислении опорных точек эквидистанты различают три типовых случая сопряжения дугой (радиусом R_И) участков эквидистанты: прямая — прямая, прямая — окружность и окружность — окружность (см. рис. 5.2, в). Как уже говорилось, координаты опорных точек траектории инструмента чаще всего рассчитывают путем определения приращений координат опорных точек контура детали. Для нахождения этих приращений существуют определенные зависимости.

Рис. 5.2. Участки эквидистанты

Трудоемкость вычисления координат опорных точек при ручном программировании во многом зависит от опыта технолога-программиста, его знаний и способности ориентироваться при постановке и решении геометрических задач. Систематизация встречающихся геометрических задач и способов их решения не исключает индивидуального подхода к конкретной задаче, что часто позволяет найти более простое ее решение Ускоряет решение задач и использование справочной литературы, содержащей типовые примеры геометрических построений.

^ Особенности расчета с использованием компьютера. Трудоемкость процесса определения координат опорных точек существенно снижается при использовании персональных компьютеров. Они имеют математическое обеспечение в виде различных систем подготовки УП. В простых системах язык системы содержит определенное число вычислительных процедур и позволяет решать задачи по определению точек стыков геометрических элементов траектории перемещения центра инструмента. Мощные системы автоматически определяют любые самые сложные эквидистанты в трехмерном измерении, получение которых ручными расчетами невозможно. Обычно исходные данные вводят через клавиатуру печатающего устройства или дисплея, или же автоматически считываются с элементов объекта производства.

При использовании ЭВМ можно также решать ряд других задач, например рассчитывать частоты вращения шпинделя на каждом переходе при заданной скорости, находить максимально допустимый крутящий момент, определять скорости подачи по контуру, автоматически получать схемы и режимы обработки по заданной точности и шероховатости, автоматически обеспечить выбор режущего инструмента и др. Достаточно прост при этом не только вывод рассчитываемой траектории на графопостроитель, но и автоматическое получение УП в целом, видеопросмотр на экране разработанной схемы удаления припуска с заготовки с указанием недоработанных мест (например, зарезов инструмента) и т.д.
^