Устойчивость автоматических систем

Структурная схема системы

 

Для анализа динамических характеристик в большинстве случаев значительно быстрее, проще и полезнее математическое описание автоматической системы формировать не на основе системы уравнений элементов, а путем построения так называемой структурной схемы при помощи аппарата передаточных функций типовых звеньев. Структурная (алгоритмическая) - схема - это условное графическое изображение автоматической системы. Она характеризует геометрию системы, пути распространения сигналов, определяет из каких динамических звеньев состоит автоматическая система и как они связаны между собой. На структурную схему наносятся условными знаками все динамические звенья в виде прямоугольника с обозначением их передаточных функций, связей и направлений распространения сигналов в виде стрелок, точек разветвления и сумматоров сигналов, изображения входной и выходной величин, изображения внешних воздействий.

Таким образом, структурная схема показывает строение автоматической системы, наличие внешних воздействий и точки их приложения, пути распространения воздействий, входную и выходную величины. По структурной схеме можно составить математическое описание автоматической системы, составить передаточную функцию всей системы и построить график переходного процесса. При таком начертании структурная схема автоматической системы представляет собой графическое изображение системы дифференциальных уравнений, описывающих работу автоматической системы. Графическое изображение предпочтительнее обычной математической записи уравнений, так как позволяет весьма просто и, пользуясь формальными единообразными правилами, производить "свертывание" этих уравнений для получения математической модели системы (передаточной функции всей системы) в удобной для анализа форме.

На рис. 3.1 и 3.2 показан пример структурной схемы автоматической системы регулирования скорости вращения электрического двигателя.

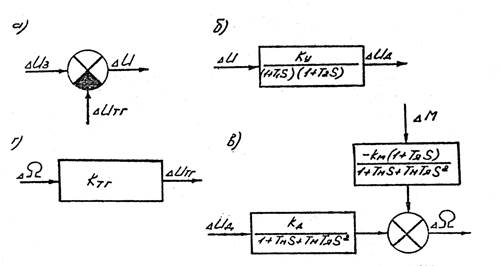
Рис. 3.1. Передаточные функции звеньев системы регулирования скорости вращения электрического двигателя.

 

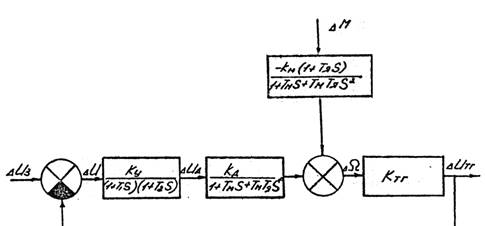
Рис.3.2. Структурная схема автоматической системы регулирования скорости вращения электрического двигателя.

 

Составление схемы удобно начинать с изображения задающего воздействия и располагать динамические звенья в прямой связи слева направо до регулируемой величины, а затем (или одновременно) показывать местные и главную обратные связи.

Существует три основных типа соединений динамических звеньев:

- последовательное соединение двух и более звеньев,

- параллельное соединение двух звеньев с общим входом.

- встречно-параллельное соединение звеньев или соединение звеньев с обратной связью.

Каждое типовое соединение звеньев можно заменить одним эквивалентным звеном с соответствующей эквивалентной передаточной функцией по установленным правилам. Для типовых соединений такая передаточная функция равна;

а) при последовательном соединении - произведению передаточных функций звеньев

 

W(S) = ПⁿW_i,(S); (3.1)

ⁱ⁼¹

б) при параллельном соединении (входная величина одна и та же для всех элементов данного соединения, а выходные величины разные и суммируется) ^: - сумме передаточных функций звеньев.

 

W(S) = åⁿ Wi(S); (3.2)

i =1

 

в) при встречно - параллельном соединении (с отрицательной обратной связью) сигнал Y(s) с выхода звена с передаточной функцией W(S) подается обратно на его вход через другое звено с передаточной функцией W₂(S) как показано на рис.3.3. Здесь на входе мы имеем сумму сигналов X(s) – W₂(S) Y(S). По определению передаточной функции для элемента в прямой связи

 

W(S) = Y(S)/[Х(S) - W₂(s)*Y(S)]

 

Отсюда передаточная функция такого соединения равна:

 

W(S) = W₂(S)/[l – W₁(S)W₂(S)] (3.3)

 

Таким образом, эквивалентная передаточная функция встречно-параллельного соединения равна дроби, числитель которой -произведение передаточных функций прямой связи, а знаменатель -произведение передаточных функций пряхой и обратной связей, взятое с противоположным знаком сумматору в обратной связи, плюс единица.

В структурных схемах могут быть и другие соединения звеньев, которые отличаются от типовых соединений и по ним нельзя составить эквивалентную передаточную функцию. В этом случае производят преобразования отдельных частей структурной схемы для получения типовых соединений звеньев. Имеется много правил преобразования не типовых соединений звеньев. Рассмотрим некоторые из них. На рис.3.4 показаны схемы следующих преобразований:

а) Перенос точки разветвления через звено с добавление в ответв­ляющуюся связь звена, через которое переносили эту точку разветв­ления (Рис.3.4а и 3.4б): звено с передаточной функцией 1/W(S) при переносе по направлению распространения сигнала и звено с пере­даточной функцией W(S) при переносе против направления распрост­ранения сигнала.

б) Перенос сумматора через звено с добавлением в ответвляющуюся связь звена, через которое переносили сумматор (Рис.3.4в и 3.4г):

· звено с передаточной функцией W(S) при переносе по направлению распространения сигнала и

· звено с передаточной функцией l/W(S) при переносе против направления распространения сигнала.

Перестановка между собой соседних точек разветвления, находящихся между звеньями не приводит к изменению схемы. При перестановке между собой соседних сумматоров схема также не изменяется.

Преобразование структурных схем должно осуществляться в следующей последовательности:

1) Замена каждого типового соединения звеньев в схеме эквивалёнтным звеном, выражая его эквивалентной передаточной функцией через передаточные функции типовых звеньев.

2) Последовательное преобразование не типовых соединений звеньев в типовые соединения звеньев с последующим их преобразованием.

Каждая операция выполняется последовательно одна за другой до получения эквивалентной одноконтурной схемы, по которой составляется передаточная функция всей системы.

Здесь рассмотрены простейшие структурные преобразования. Обычно с их помощью удается многоконтурную структурнуюсхему привестик одноконтурной.

Рис.3.3. Встречно – параллельное соединение звеньев.

Рис.3.4. перенос точек разветвления и сумматоров.

3.2. Некоторые передаточные функции линейных систем.

 

При расчете и анализе автоматических систем составляют передаточные функции относительно различных выходных величин:

выходной величины всей системы, задавшего воздействия, каждого из возмущений, для ошибки слежения. Найдем значенияэтих передаточных функций для структурной схемы, показанной на рис.3.5.

Рис.3.5. Структурная схема.

1) Для разомкнутой системы, которая разомкнута околоэлемента сравнения (сумматора С1):

 

W(s) = Y_o(s)/X(s) = W₁(s) W₂(s) W_o(S). (3.4)

 

Где Y₀(s) - изображение сигнала обратной связи, X(s) - изображение задавшего воздействия. Эта передаточная функция характеризует собственные динамические свойства системы и по ней определяет ее устойчивость.

2) Для замкнутой системы относительно входного воздействияХ(s)предполагая, что других внешних воздействий нет:

 

W(s) = Y(s)/X(s) = W₁(s)W₂(s)/[1+W₁(s)W₂(s)W₀(s) (3.5)

 

где Y(s) - изображение регулируемой величины. X(s) - изображение задавшего воздействия.

Эта передаточная функция характеризует передачу системой задавшего воздействия, его воспроизведение регулируемой величиной.

3) Для замкнутой системы по ошибке сложения, предполагая,что других внешних воздействий нет:

 

W(S) = Х_D(S)/Х(S) = 1/[1 + W₁(S) W₂(S) W₀(S)]. (3.6)

 

где Х_D(S) - изображение рассогласования Х_D(S) = X(s) - Yo(S).

Здесь в прямой связи нет звеньев.Формула характеризует воспроизведение регулируемой величиной заданного воздействия. Воспроизведение тем лучше,чем ближе значение W(s) к идеальному, то есть нулю.

4) Для замкнутой системы относительно возмущения Z(s) при отсут­ствии других внешних воздействий:

 

W(s) = Y(s)/Z(s) = W(s)/[l + W₁(s) W₂(s) W₀(s)] (3.7)

 

где Z(s) - изображение возмущения.

Формула показывает влияние возмущения на регулируемую величину. Возмущение отклоняет ее от заданного значения и уменьшает точность воспроизведения задающего воздействия. Если на систему воздействует несколько возмущений, то передаточная функция определяется относительно каждогоиз них.

5) Для системы относительно задающего воздействия X(s) и возму­щения Z(s):

 

Y(s) = W_x(s)X(s) + W₂(s) Z(s). (3.8)

 

3.3. Метод определения характеристики переходного процесса

 

Определение переходного процесса автоматической системы,тоесть построение временной характеристики выходной величины Y =Y(t)производится в следующей последовательности:

1) Произвести преобразование структурной схемы системы в одноконтурную структурную схему по вышеизложенным правилам (раздел3.1).

2) Составить передаточную функцию всей системы.

Полученную эквивалентную передаточную функцию системы выражаем через передаточные функции всех динамических звеньев.

 

3) Каждая передаточная функция в полученном выражении записывается через числовые величины. Полученная передаточная функция имеет вид правильной рациональной дроби [3]. Если дробь непра­вильная (степень числителя выше степени знаменателя), то для полу­чения правильной дроби необходимо разделить числитель на знаме­натель по правилам деления многочлена, результат деления получится в виде суммы многочлена и правильной дроби.

4) Полученную правильную дробь необходима разложить на простые дроби (по правилам неопределенных коэффициентов), соответствующие табличным функциям изображений Лапласа. Такие простые дроби можно представить в виде суммы следующих простейших дробей:

 

a/s-a, As+B/(s² + a1s + a2)

a/(s-a)^k As+B/(s² + a1s + a2)^k

 

где К - целое положительное число,К > 2,

корни знаменателя (s^k- a1s+a2) - комплексные, а s²/4 - а < 0.

Разлагая любую правильную дробь на простейшие методом неопределенных коэффициентов, получим сумму простейших дробей, соот­ветствующих табличным изображениям Лапласа.

Ниже на примере показан порядок разложения правильной рациональ­ной дроби.

Пусть имеется передаточная функция

H(s) = (3s + 2)/(0.2s + 1) s³ [2].

 

1) Разлагаем данную дробь на простейшие дроби

 

3s+2/(0.2s+1)s³ = a₁/s + a₂/s² + a_3/s³ + b/(0.2s+1)

 

2) Приводим уравнение к общему знаменателю и отбрасываем его

 

3s + 2 = a₁s²(0.2 + 1) + a₂s(0.2s + 1) + a₃(0.2 + 1) + bs³

3) Приравниваем коэффициенты левой и правой частей уравнения при равных степенях переменной s. Если в левой части уравнения соответствующих степеней нет, то коэффициент в правой части приравнивается нулю. В нашем примере получим следующие равенства:

 

A₃ =2;

A₂ +0.2 A₃ = 3;

A₁ + 0.2A₂ = 0;

0.2A₁ + B = 0.

 

4) Откуда значения этих коэффициентов будут:

 

A₁ = -0.52; A₂ = 2.6; A₃ = 2; B = 0.104.

5) Тогда передаточная функция выразится в следующем виде:

 

W(s) = 0.52/s + 2.6/s² + 2/s³ + 0.104/(0.25s + 1)

 

6) После этого для каждого члена уравнения в операторной форме находим по таблице Лапласа (см. табл. 2.1) оригинал и, таким образом, получаем окончательное уравнение оригинала по переменной время t:

 

. Y(t) = 0.52 + 2,6t + 0.52e ^–5t + 2t².

 

7) По этому уравнениястроится график переходного процесса.

 

 

Таблица 4.1

Коэффи -циент К	№ строки	№ столбца
-		A0	A2	A4
-		A1	A3	A5
K13 = A0 / A1		C23 = A2 – K13 A3	C33 = A4 – K13 A5	C43 = 0
K14 = A1 / C23		C24 = A3 – K14 C33	C34= A5 - 0	C44 = 0
K15 = C23 / C24		C25 = C33 – K15 C34	C35 = 0	C45 = 0
K16 = C24 / C25		C26 = C34 = A5	C36 = 0	C46 = 0

 

Система устойчива, если все коэффициенты первого столбца были положительны, то есть

 

A₀ > 0. A₁ > 0. C₂₃ > 0. C₂₄ > 0. C₂₅ > 0. C₂₆ > 0.

 

3) Критерий устойчивости Михайлова. Этот частотный критерий устойчивости был введен в 1938г. А.В.Михайловым. Из существующих частотных методов этот метод получил наибольшее распространение. Анализ устойчивости системы сводится к построению по характеристическому уравнению характеристической кривой или годографа, по виду которого можно судить о состоянии системы сточкизрения устойчивости.

Годограф рассчитывается и строится следующим образом (рассмотрим пример для уравнения пятого порядка согласно уравнения (4.5):

а) Заменяем в данном уравнении комплексную переменную sна выражение (iw)

 

A₀ (jw)⁵ + A₁ (jw)⁴ + A₂(jw)³ + A₃ (jw)² + A₄ (jw) + A₅ = 0.

 

б) Возводим члены (jw) полученного уравнения в соответствующие степени

 

A₀ jw⁵ + A₁ w⁴ - A₂ jw³ – A₃ w² + A₄ jw + A₅ = 0.

 

в) Разделяем вещественные и мнимые части полученного многочлена и выписываем их отдельно друг от друга

 

Re(w) = A₅ - A₃ w² + A₁ w⁴ - вещественные части,

Jm(w) = A₄ w – A₂ w³ + A₀ w⁵ - мнимые части.

 

г) Подсчитываем величины Re(w) и Jm(w) для каждого значения w от О до + бесконечности.

д) Строим годограф на комплексной плоскости, то есть кривую по расчетным величинам Re(w) и Jm(w) для соответствующих значений частот w_1, w₂, w₃…. и так далее. Через полученные точки проводим кривую, которая и является годографом Михайлова. При этом удобно вначале находить точки пересечения годографа с осями координат. Для точек на вещественной оси принимаем Jm(w) = 0 откуда находят значения частот, которые затем подставляют в выражение для Re(w).

Полученные при этом значения Re(w). являются абсциссами точек пересечения годографа с вещественной осью. Затем для точек на мнимой оси принимаем Re(w) = 0, и далее аналогично.

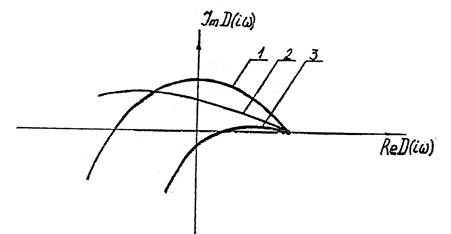
Критерий Михайлова пригоден для анализа устойчивости систем любого порядка. На рисунке рис.4.2. показаны примеры трех годографов;

1 - для устойчивой системы, 2 и 3 - для неустойчивых систем.

Рис.4.2. Годографы Михайлова.

 

Автоматическая система устойчива, если годографпри изменении частоты и от 0 до + бесконечности:

а) начинается на положительной части вещественной оси:

б) обходит в направлении против часовой стрелки последовательно такое количество квадрантов комплексной плоскости, какова степень характеристического уравнения:

в) нигдене обращается в нуль.

 

Пневматический клапан

 

Пневматический клапан (рис.5.1) является однимиз основных элементов пневматических систем управления. От правильного выбора его параметров зависит быстродействие пневматического привода, устойчивость его работы, качество переходного процесса. При рассмотрении динамики клапана пренебрегаем теплообменом с окружающей средой.

По законам газовой динамики скорость изменения давления воздуха в исполнительном элементе (на выходе из клапана)при малых открытиях клапана будет определяться

 

dp_k/dt = KX (5.3)

 

 

где X - перемещение (величина открытия)-клапана.

К = f(p.q.U) - коэффициент усиления клапана, зависящий от:

р - давления воздуха в полости источника давления (ресивере);

q - отношения давления воздуха в полости за клапаном к давлению

р (обычно при рассмотрении динамики систем особый интерес

представляет случай 0 < q < 0.5282 - критический режим истечения, при

котором f(q) = const).

U - объем емкости, куда происходит истечение воздуха.

Риc.5.1. Пневматический клапан.

Х - перемещение клапана.

Рк - давление воздуха на выходе из клапана,

Р -давление воздуха на входе в клапан.

При р = const. U = const. f(q) = const параметр К есть величина постоянная и дифференциальное уравнение в операторной форме для пневматического клапана будет

 

s p_k (s) = К X(s). (5.4)

 

Тогда, полагая X(s) - изображение входного параметра, a p(s) -изображение выходного параметра, передаточная функция имеет вид:

 

W(s) = p_k (s)/X(s) = K/s. (5.5)

 

то есть пневматический клапан при такой моделировании может быть описан интегрирующим звеном.

 

Исполнительный элемент

 

В качестве исполнительных элементов чаде всего используют гидравлические и пневматические поршневые цилиндры и мембранные камеры. Здесь выходной параметр - перемещение штока, а входная величина – давление, подаваемое в рабочую полость.

Тогда передаточная функция элемента будет иметьвид

 

W(s) = X(s)/p(s) = f/(m s² + v s + с). (5.6)

 

где m - масса подвижных частей исполнительного механизма.

f - эффективная площадь поршня.

u - коэффициент вязкого трения

с - жесткость возвратной пружины.

 

Центробежный механизм

 

На автомобилях и тракторах центробежные механизмы используются весьма широко: в автоматизированных приводах сцеплений, центробежных сцеплениях, системе зажигания карбюраторных двигателей, регуляторах частот вращения двигателей, автоматических гидропередачах.

Центробежные механизмы имеют такие положительные свойства,какполучение больших усилий на управляющем органе, простота конструкции, надежность, стабильность в работе (на работу не влияют окружающая температура, давление воздуха, вибрации), большое быстродействие, малая приводная мощность. Они широко применятся в регуляторах давления и других следящих устройствах. Бывают двух типов: рычажный и безрычажный.

На рис.5.2 показан рычажный центробежный механизм. Из условия равновесия грузов сила. приложенная к штоку механизма в результате действия центробежной силы грузов будет иметь вид

 

F = Fu w R i

 

где i - передаточное число рычагов.

Центробежные механизмы могут проектироватьсятак, что

а) R i = const.

б) R i ¹ const.

 

Рис.5.2. Схема рычажного центробежного механизма.

Рассмотрим оба случая.

1 случай: Ri = const. Тогда при изменении частоты вращенияна

dw (w = w₀ + dw) можно написать дифференциальное уравнение в приращениях следующим образом:

 

m(dX)ⁿ + v dX)¹ + c(dX) = dF (5.7)

 

где m - приведенная масса поступательно - движущихся частей: v - коэф­фициент вязкого трения; с - жесткость возвратной пружины. С учетом того, что dF = m Ri (dw)² = m Ri 2 w₀ dw, преобразуем дифференциальное уравнение по переменной время t и, преобразовав последнее уравнение в уравнение в операторной форме по переменной s:

 

(mS² + vS + c) X (s) = 2m Ri w₀ w(s) = K w(s)

 

где К = 2m, Ri w₀ - коэффициент усиления центробежногомеха­низма. Тогда передаточная функция центробежного механизма будет иметь вид -

 

W(s) = X(s)/w(s) = K/(ms² + vs + c) (5.8)

 

 

из чего следует,что центробежный механизм являетсяколебательным звеном.

Полученную передаточную функцию можно представить в видедвухпоследовательно соединенных типовых динамических звеньев:

- усилительного с передаточной функцией W (s) = F (s)/W(s)= К,

- колебательного W (s) = X(s)/F (s) = 1/(ms² + vs + с).

Условие устойчивости центробежного механизма можно определить по критерию Гурвица как для уравнения третьего порядка

m > 0, v > О, с > 0.

Отсюда видно, что такой центробежный механизм всегда устойчив.

Условия, при которых Ri = const. Из схемы для рычажного центробежного механизма имеем:

 

R = h + r Sin(a); а = r Cos(a); и i = r Cos(a)/b; i= а/b.

Тогда Ri = {[h + г Sin(a)] r Cos(a)}/b,

откуда Ri b/r = (h/r) Cos(a) + Sin(a) Cos(a).

 

Для получения условий, при которых Ri = const.найдем производную полученного выражения по углу (a) и приравниваемее кнулю:

 

(h/r)(-Sin(a)) + Cos(a) Cos(a) - Sin(a)Sin(a) =

= - (h/r) Sin(a) + Cos2(a) =0

 

Так как отношение h/r > 0, то всегда угол (a) < 45. После расчета, получим следующую таблицу:

 

отношение h/r 0.5 1.0 2.0 3,0 4.0 ¥

угол (a) 37 30 26 22 17 0

 

2 случай: Ri ¹ const. но i = const. Тогда можно записать

 

dF = d(m Ri w) = m i R d(w) + m i w₀ d(R)

 

Далее полагая, что при малых перемещениях штока

 

R= Xi

 

иподставляя все в дифференциальное уравнение получим

 

m(dX)ⁿ + v (dX) + (c – m iw₀) (dX) = 2mRi w₀d(w)

 

Здесь 2mRiw₀ = Km-.коэффициент усиления центробежного механизма, а (с – m i w₀) = C₃ - эквивалентная жесткость пружины на штоке центробежного механизма.

Тогда передаточная функция такого центробежного механизма будет иметь вид

 

W() = X(s)/w(s) = K_m /(ms + vs + с₃) (5.9)

 

Таким образом, для центробежного механизма с Ri ¹ const вместо С следует рассматривать С₃- эквивалентную жесткость пружины, которая называется коэффициентом самовыравнивания или фактором устойчивости, так как для устойчивости необходимо, чтобы:

(c – m i w₀) > 0, то есть с > m i w₀.

Следовательно только при определенных значениях параметров с, m, i и w₀ центробежный меха­низм будет устойчив.

 

Структурная схема системы

 

Для анализа динамических характеристик в большинстве случаев значительно быстрее, проще и полезнее математическое описание автоматической системы формировать не на основе системы уравнений элементов, а путем построения так называемой структурной схемы при помощи аппарата передаточных функций типовых звеньев. Структурная (алгоритмическая) - схема - это условное графическое изображение автоматической системы. Она характеризует геометрию системы, пути распространения сигналов, определяет из каких динамических звеньев состоит автоматическая система и как они связаны между собой. На структурную схему наносятся условными знаками все динамические звенья в виде прямоугольника с обозначением их передаточных функций, связей и направлений распространения сигналов в виде стрелок, точек разветвления и сумматоров сигналов, изображения входной и выходной величин, изображения внешних воздействий.

Таким образом, структурная схема показывает строение автоматической системы, наличие внешних воздействий и точки их приложения, пути распространения воздействий, входную и выходную величины. По структурной схеме можно составить математическое описание автоматической системы, составить передаточную функцию всей системы и построить график переходного процесса. При таком начертании структурная схема автоматической системы представляет собой графическое изображение системы дифференциальных уравнений, описывающих работу автоматической системы. Графическое изображение предпочтительнее обычной математической записи уравнений, так как позволяет весьма просто и, пользуясь формальными единообразными правилами, производить "свертывание" этих уравнений для получения математической модели системы (передаточной функции всей системы) в удобной для анализа форме.

На рис. 3.1 и 3.2 показан пример структурной схемы автоматической системы регулирования скорости вращения электрического двигателя.

Рис. 3.1. Передаточные функции звеньев системы регулирования скорости вращения электрического двигателя.

 

Рис.3.2. Структурная схема автоматической системы регулирования скорости вращения электрического двигателя.

 

Составление схемы удобно начинать с изображения задающего воздействия и располагать динамические звенья в прямой связи слева направо до регулируемой величины, а затем (или одновременно) показывать местные и главную обратные связи.

Существует три основных типа соединений динамических звеньев:

- последовательное соединение двух и более звеньев,

- параллельное соединение двух звеньев с общим входом.

- встречно-параллельное соединение звеньев или соединение звеньев с обратной связью.

Каждое типовое соединение звеньев можно заменить одним эквивалентным звеном с соответствующей эквивалентной передаточной функцией по установленным правилам. Для типовых соединений такая передаточная функция равна;

а) при последовательном соединении - произведению передаточных функций звеньев

 

W(S) = ПⁿW_i,(S); (3.1)

ⁱ⁼¹

б) при параллельном соединении (входная величина одна и та же для всех элементов данного соединения, а выходные величины разные и суммируется) ^: - сумме передаточных функций звеньев.

 

W(S) = åⁿ Wi(S); (3.2)

i =1

 

в) при встречно - параллельном соединении (с отрицательной обратной связью) сигнал Y(s) с выхода звена с передаточной функцией W(S) подается обратно на его вход через другое звено с передаточной функцией W₂(S) как показано на рис.3.3. Здесь на входе мы имеем сумму сигналов X(s) – W₂(S) Y(S). По определению передаточной функции для элемента в прямой связи

 

W(S) = Y(S)/[Х(S) - W₂(s)*Y(S)]

 

Отсюда передаточная функция такого соединения равна:

 

W(S) = W₂(S)/[l – W₁(S)W₂(S)] (3.3)

 

Таким образом, эквивалентная передаточная функция встречно-параллельного соединения равна дроби, числитель которой -произведение передаточных функций прямой связи, а знаменатель -произведение передаточных функций пряхой и обратной связей, взятое с противоположным знаком сумматору в обратной связи, плюс единица.

В структурных схемах могут быть и другие соединения звеньев, которые отличаются от типовых соединений и по ним нельзя составить эквивалентную передаточную функцию. В этом случае производят преобразования отдельных частей структурной схемы для получения типовых соединений звеньев. Имеется много правил преобразования не типовых соединений звеньев. Рассмотрим некоторые из них. На рис.3.4 показаны схемы следующих преобразований:

а) Перенос точки разветвления через звено с добавление в ответв­ляющуюся связь звена, через которое переносили эту точку разветв­ления (Рис.3.4а и 3.4б): звено с передаточной функцией 1/W(S) при переносе по направлению распространения сигнала и звено с пере­даточной функцией W(S) при переносе против направления распрост­ранения сигнала.

б) Перенос сумматора через звено с добавлением в ответвляющуюся связь звена, через которое переносили сумматор (Рис.3.4в и 3.4г):

· звено с передаточной функцией W(S) при переносе по направлению распространения сигнала и

· звено с передаточной функцией l/W(S) при переносе против направления распространения сигнала.

Перестановка между собой соседних точек разветвления, находящихся между звеньями не приводит к изменению схемы. При перестановке между собой соседних сумматоров схема также не изменяется.

Преобразование структурных схем должно осуществляться в следующей последовательности:

1) Замена каждого типового соединения звеньев в схеме эквивалёнтным звеном, выражая его эквивалентной передаточной функцией через передаточные функции типовых звеньев.

2) Последовательное преобразование не типовых соединений звеньев в типовые соединения звеньев с последующим их преобразованием.

Каждая операция выполняется последовательно одна за другой до получения эквивалентной одноконтурной схемы, по которой составляется передаточная функция всей системы.

Здесь рассмотрены простейшие структурные преобразования. Обычно с их помощью удается многоконтурную структурнуюсхему привестик одноконтурной.

Рис.3.3. Встречно – параллельное соединение звеньев.

Рис.3.4. перенос точек разветвления и сумматоров.

3.2. Некоторые передаточные функции линейных систем.

 

При расчете и анализе автоматических систем составляют передаточные функции относительно различных выходных величин:

выходной величины всей системы, задавшего воздействия, каждого из возмущений, для ошибки слежения. Найдем значенияэтих передаточных функций для структурной схемы, показанной на рис.3.5.

Рис.3.5. Структурная схема.

1) Для разомкнутой системы, которая разомкнута околоэлемента сравнения (сумматора С1):

 

W(s) = Y_o(s)/X(s) = W₁(s) W₂(s) W_o(S). (3.4)

 

Где Y₀(s) - изображение сигнала обратной связи, X(s) - изображение задавшего воздействия. Эта передаточная функция характеризует собственные динамические свойства системы и по ней определяет ее устойчивость.

2) Для замкнутой системы относительно входного воздействияХ(s)предполагая, что других внешних воздействий нет:

 

W(s) = Y(s)/X(s) = W₁(s)W₂(s)/[1+W₁(s)W₂(s)W₀(s) (3.5)

 

где Y(s) - изображение регулируемой величины. X(s) - изображение задавшего воздействия.

Эта передаточная функция характеризует передачу системой задавшего воздействия, его воспроизведение регулируемой величиной.

3) Для замкнутой системы по ошибке сложения, предполагая,что других внешних воздействий нет:

 

W(S) = Х_D(S)/Х(S) = 1/[1 + W₁(S) W₂(S) W₀(S)]. (3.6)

 

где Х_D(S) - изображение рассогласования Х_D(S) = X(s) - Yo(S).

Здесь в прямой связи нет звеньев.Формула характеризует воспроизведение регулируемой величиной заданного воздействия. Воспроизведение тем лучше,чем ближе значение W(s) к идеальному, то есть нулю.

4) Для замкнутой системы относительно возмущения Z(s) при отсут­ствии других внешних воздействий:

 

W(s) = Y(s)/Z(s) = W(s)/[l + W₁(s) W₂(s) W₀(s)] (3.7)

 

где Z(s) - изображение возмущения.

Формула показывает влияние возмущения на регулируемую величину. Возмущение отклоняет ее от заданного значения и уменьшает точность воспроизведения задающего воздействия. Если на систему воздействует несколько возмущений, то передаточная функция определяется относительно каждогоиз них.

5) Для системы относительно задающего воздействия X(s) и возму­щения Z(s):

 

Y(s) = W_x(s)X(s) + W₂(s) Z(s). (3.8)

 

3.3. Метод определения характеристики переходного процесса

 

Определение переходного процесса автоматической системы,тоесть построение временной характеристики выходной величины Y =Y(t)производится в следующей последовательности:

1) Произвести преобразование структурной схемы системы в одноконтурную структурную схему по вышеизложенным правилам (раздел3.1).

2) Составить передаточную функцию всей системы.

Полученную эквивалентную передаточную функцию системы выражаем через передаточные функции всех динамических звеньев.

 

3) Каждая передаточная функция в полученном выражении записывается через числовые величины. Полученная передаточная функция имеет вид правильной рациональной дроби [3]. Если дробь непра­вильная (степень числителя выше степени знаменателя), то для полу­чения правильной дроби необходимо разделить числитель на знаме­натель по правилам деления многочлена, результат деления получится в виде суммы многочлена и правильной дроби.

4) Полученную правильную дробь необходима разложить на простые дроби (по правилам неопределенных коэффициентов), соответствующие табличным функциям изображений Лапласа. Такие простые дроби можно представить в виде суммы следующих простейших дробей:

 

a/s-a, As+B/(s² + a1s + a2)

a/(s-a)^k As+B/(s² + a1s + a2)^k

 

где К - целое положительное число,К > 2,

корни знаменателя (s^k- a1s+a2) - комплексные, а s²/4 - а < 0.

Разлагая любую правильную дробь на простейшие методом неопределенных коэффициентов, получим сумму простейших дробей, соот­ветствующих табличным изображениям Лапласа.

Ниже на примере показан порядок разложения правильной рациональ­ной дроби.

Пусть имеется передаточная функция

H(s) = (3s + 2)/(0.2s + 1) s³ [2].

 

1) Разлагаем данную дробь на простейшие дроби

 

3s+2/(0.2s+1)s³ = a₁/s + a₂/s² + a_3/s³ + b/(0.2s+1)

 

2) Приводим уравнение к общему знаменателю и отбрасываем его

 

3s + 2 = a₁s²(0.2 + 1) + a₂s(0.2s + 1) + a₃(0.2 + 1) + bs³

3) Приравниваем коэффициенты левой и правой частей уравнения при равных степенях переменной s. Если в левой части уравнения соответствующих степеней нет, то коэффициент в правой части приравнивается нулю. В нашем примере получим следующие равенства:

 

A₃ =2;

A₂ +0.2 A₃ = 3;

A₁ + 0.2A₂ = 0;

0.2A₁ + B = 0.

 

4) Откуда значения этих коэффициентов будут:

 

A₁ = -0.52; A₂ = 2.6; A₃ = 2; B = 0.104.

5) Тогда передаточная функция выразится в следующем виде:

 

W(s) = 0.52/s + 2.6/s² + 2/s³ + 0.104/(0.25s + 1)

 

6) После этого для каждого члена уравнения в операторной форме находим по таблице Лапласа (см. табл. 2.1) оригинал и, таким образом, получаем окончательное уравнение оригинала по переменной время t:

 

. Y(t) = 0.52 + 2,6t + 0.52e ^–5t + 2t².

 

7) По этому уравнениястроится график переходного процесса.

 

 

УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ