Косвенные методы оценки устойчивости

 

Алгебраические критерии устойчивости предложены Э.Раусом в 1877г. и А.Гурвицем в 1895г. С помощью этих критериев определяется соотношение между коэффициентами характеристического уравнения. Для рассмотрения обоих критериев возьмем характеристическое уравнение пятого порядка:

 

A₀ s⁵ + A₁s⁴ + A₂s³ + A₃s² + A₄s = 0 (4.5)

 

1) Критерий Гурвица.Из коэффициентов характеристического уравнения (4.5) составляют матрицу Гурвица следующего вида:

 

 

A1	A3	A5
A	A2	A4
	A1	A3	A5
	A	A2	A4
		A1	A3	A5

 

Матрица составляется следующим образом:

1) Главная диагональ -из коэффициентов характеристического уравнения начиная с А₁ до А_5.

2) Строки - из коэффициентов этого уравнения: справа от главной диагонали - в порядке увеличения индекса через единицу; слева от главной диагонали в порядке уменьшения индексов. При этом коэффициенты с индексами, превышающими порядок характеристического уравнения и коэффициенты с отрицательными индексами заменяются нулями.

Для выполнения условия устойчивости необходимо и достаточно, чтобы все диагональные миноры (определители Гурвица) матрицы были положительны, то есть

 

A1

A3

A1

A3

A5

A1

>

0;

>

0;

A0

A2

A4

>

0;

A0

A2

A1

A3

 

Тогда условия устойчивости можно сформулировать в виде:

а) Для уравнений первого и второго порядка – положительностьвсех коэффициентов характеристического уравнения. Это условиетакженеобходимо для уравнения любого высшего порядка.

 

б) Для уравнения третьего порядка:

 

(A₁ A₂ > A₀ A₃)

в) Для уравнения четвертого порядка:

 

(A₁ A₂ A₃ > A₀ A²₃ + A²₁ A₄)

г) Для уравнения пятого порядка:

 

(A₁ A₂ - A₀ A₃)(A₃ A₄ – A₂ A₅) > (A₁ A₄ – A₀ A₅)²

2) Критерий Рауса. По этому критерию необходимо составитьтаблицуРаусаиз коэффициентов характеристического уравнения приА₀ > 0.Такая таблица для характеристического уравнения (4.5) будетиметь следующий вид.

Таблица заполняется следующим образом:

а) Первая и вторая строки - из коэффициентовс четными и снечетными индексами, соответственно.

б) Остальные строки - из расчетных коэффициентов табл. 4.1.

в) Таблица заполняется до тех пор, пока при заданном уравнениине получится строка, содержащая значащий коэффициент, соответствующий свободному члену уравнения только в первом столбце.

 

 

Таблица 4.1

Коэффи -циент К	№ строки	№ столбца
-		A0	A2	A4
-		A1	A3	A5
K13 = A0 / A1		C23 = A2 – K13 A3	C33 = A4 – K13 A5	C43 = 0
K14 = A1 / C23		C24 = A3 – K14 C33	C34= A5 - 0	C44 = 0
K15 = C23 / C24		C25 = C33 – K15 C34	C35 = 0	C45 = 0
K16 = C24 / C25		C26 = C34 = A5	C36 = 0	C46 = 0

 

Система устойчива, если все коэффициенты первого столбца были положительны, то есть

 

A₀ > 0. A₁ > 0. C₂₃ > 0. C₂₄ > 0. C₂₅ > 0. C₂₆ > 0.

 

3) Критерий устойчивости Михайлова. Этот частотный критерий устойчивости был введен в 1938г. А.В.Михайловым. Из существующих частотных методов этот метод получил наибольшее распространение. Анализ устойчивости системы сводится к построению по характеристическому уравнению характеристической кривой или годографа, по виду которого можно судить о состоянии системы сточкизрения устойчивости.

Годограф рассчитывается и строится следующим образом (рассмотрим пример для уравнения пятого порядка согласно уравнения (4.5):

а) Заменяем в данном уравнении комплексную переменную sна выражение (iw)

 

A₀ (jw)⁵ + A₁ (jw)⁴ + A₂(jw)³ + A₃ (jw)² + A₄ (jw) + A₅ = 0.

 

б) Возводим члены (jw) полученного уравнения в соответствующие степени

 

A₀ jw⁵ + A₁ w⁴ - A₂ jw³ – A₃ w² + A₄ jw + A₅ = 0.

 

в) Разделяем вещественные и мнимые части полученного многочлена и выписываем их отдельно друг от друга

 

Re(w) = A₅ - A₃ w² + A₁ w⁴ - вещественные части,

Jm(w) = A₄ w – A₂ w³ + A₀ w⁵ - мнимые части.

 

г) Подсчитываем величины Re(w) и Jm(w) для каждого значения w от О до + бесконечности.

д) Строим годограф на комплексной плоскости, то есть кривую по расчетным величинам Re(w) и Jm(w) для соответствующих значений частот w_1, w₂, w₃…. и так далее. Через полученные точки проводим кривую, которая и является годографом Михайлова. При этом удобно вначале находить точки пересечения годографа с осями координат. Для точек на вещественной оси принимаем Jm(w) = 0 откуда находят значения частот, которые затем подставляют в выражение для Re(w).

Полученные при этом значения Re(w). являются абсциссами точек пересечения годографа с вещественной осью. Затем для точек на мнимой оси принимаем Re(w) = 0, и далее аналогично.

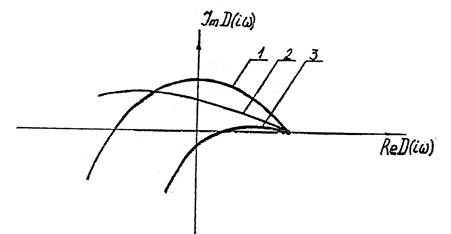
Критерий Михайлова пригоден для анализа устойчивости систем любого порядка. На рисунке рис.4.2. показаны примеры трех годографов;

1 - для устойчивой системы, 2 и 3 - для неустойчивых систем.

Рис.4.2. Годографы Михайлова.

 

Автоматическая система устойчива, если годографпри изменении частоты и от 0 до + бесконечности:

а) начинается на положительной части вещественной оси:

б) обходит в направлении против часовой стрелки последовательно такое количество квадрантов комплексной плоскости, какова степень характеристического уравнения:

в) нигдене обращается в нуль.