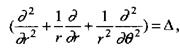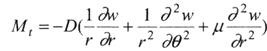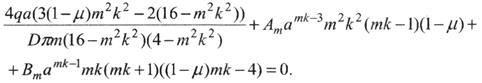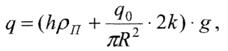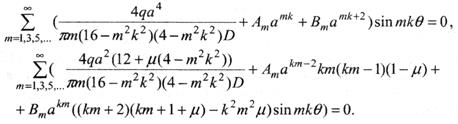Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ндс неметаллических понтонов на опоре в форме многолучевойСодержание книги
Поиск на нашем сайте
Звезды
Понтон должен быть проверен на выполнение условий прочности. Рассмотрим напряженно-деформированное состояние понтона при его установке на опорную конструкцию, которая имеет форму многолучевой звезды (рис. 7.1). Для проверки прочности плавающего покрытия достаточно рассмотреть его часть в виде сектора с центральным углом, равным углу между лучами опоры, свободно опирающуюся по краям и не опертую по дуге контура. Обозначим величину центрального угла указанного сектора через π/k. Для решения задачи применим теорию изгиба круглой пластинки. Прогиб нашего сектора будет совпадать с прогибом сектора круглой пластинки, загруженной, как показано на рис. 7.2. Положение каждой точки пластинки будет характеризоваться полярными координатами: расстоянием от центра пластинки r и углом θ. Уравнение изогнутой поверхности круглой пластинки можно записать в виде:
где q - интенсивность нагрузки, D- жесткость пластинки при изгибе.
Общее решение уравнения (7.12) представляется в виде
где w o - частное решение уравнения (7.12), a w1 - решение однородного уравнения
В случае, когда равномерно напряженная пластинка имеет вид сектора с центральным углом π/k и свободно опирается по краям, равномерно распределенная нагрузка q представляется рядом
равенство (7.15) получается заменой переменных
(где 2Т=2π/k - период функции q) из разложения в ряд Фурье аналогичной функции с периодом 2Т=2π. Дифференциальное уравнение изогнутой поверхности тогда можно представить так
(7.16)
Уравнение (7.16) получается из (7.12) подстановкой значения q из (7.15). Решение уравнения (7.16) запишем в виде
Частное решение, удовлетворяющее уравнению (7.16) возьмем в виде
Граничные условия на прямолинейных краях секториальной пластинки записываются так:
Из (7.17) получаем
при θ =0.
т.к. равенство выполняется для любого r.
Поэтому
Используя обозначение получим
Таким образом,
Граничные условия в случае свободного (неопертого) дугового контура будут такими /18/
где Мг - изгибающий момент в радиальном направлении
Qr - перерезывающая сила
Mrt - крутящий момент
а - радиус круглой пластинки. Изгибающий момент в тангенциальном направлении можно определить из соотношения
Учитывая (7.17), (7.18), (7.19), (7.22) уравнение (7.20) для определения коэффициентов Ат, Вт в (7.19) запишем так:
Подставляя значения w0 и w1 из (7.18), (7.19) в (7.21), получим второе уравнение для определения Ат,Вт.
Решая систему двух уравнений с двумя неизвестными, получим следующие значения
Подставляя полученные значения Ат, Вт в (7.19), можно определить величину прогиба в любой точке плавающего покрытия. Изгибающий момент в радиальном направлении можно определить по формуле
Величину крутящего момента можно определить по формуле
Изгибающий момент в тангенциальном направлении можно вычислить по формуле
Для напряжений максимальной величины существует зависимость /43/
где М - величина максимального момента, h - толщина плавающего покрытия. Таким образом, зная величины r, h, θ, определяя нагрузку, вызванную собственным весом плавающего покрытия и массой работающего персонала или установленного на понтоне оборудования qo no формуле
где рп - плотность материала понтона, можно определить возникающие напряжения, просуммировав большое количество членов рядов из (7.23)-(7.25). Как показывает практика, ряды сходятся быстро, и для получения заданной точности достаточно просуммировать два-три члена ряда. Ряды являются сходящимися согласно признаку Лейбница.
Пусть равномерно нагруженная пластинка имеет вид сектора с центральном углом π/k и свободно опирается по краям (в том числе по дуге контура). В работе /18/ получены аналитические выражения для определения прогибов в произвольных точках сектора с центральным углом, равным π, и при граничных условиях, соответствующих свободному опиранию по всем краям. Нами выведены решения для общего случая, когда центральный угол сектора составляет π/k рад. Рассмотрим круглую пластинку, разделенную на 2k секторов, загруженную следующим образом: 1 сектор с нагрузкой, равной по величине q, смежные с ним - с нагрузкой -q. Прогиб такой пластинки не будет отличаться от прогиба пластинки-сектора. Равномерно распределенную нагрузку разложим в ряд Фурье
Период функции Т=2π/k, поэтому коэффициенты разложениям ряд Фурье
Таким образом, дифференциальное уравнение изогнутой поверхности можно записать формулой (7.17). Выполняются также и (7.18) и (7.19). Для определения коэффициентов Ат, Вт рассмотрим сектор плавающего покрытия с центральным углом л/к, свободно опирающийся по всем краям (в том числе по дуге контура). В этом случае граничные условия будут такими
Эти уравнения, с учетом (7.17)-(7.19) можно записать так
Отсюда определяются коэффициенты
В этом случае прогиб в любой точке (г, в) можно определить по формуле
Последняя формула при k=1 совпадает с выражением для определения прогибов (6.10), полученным в [37]. Подставляя в (7.23) - (7.25) полученные по формулам (7.27) значения коэффициентов Ат, Вт, можно определить величины моментов и по формуле (7.26) вычислить величину максимального напряжения. Чтобы исследовать напряженно-деформированное состояние опирающегося на опору понтона из вспененного полимера, армированного стекло- или минераловолокнистой сеткой, можно использовать различные методики для определения жесткости многослойной круглой пластины. Если имеются хотя бы два слоя стеклосетки, повернутые один относительно другого на 90°, то такого рода пластинки можно считать монотропными (трансверсально-изотропными, транстропными), т.е. в плоскости симметрии ху свойства материала одинаковы по всем направлениям. Приведенные формулы определения НДС для них тоже справедливы [25]. Для определения прогибов в любой заданной точке, для вычисления величин моментов и соответствующих напряжений неметаллических понтонов на опоре в форме многолучевой звезды, плавучести, остойчивости и непотопляемости понтонов студентами и сотрудниками кафедры «Сооружение и ремонт ГНП и ГНХ» составлен комплекс программ на языке программирования Паскаль для IBM-совместимых ПЭВМ, включающий также программу для определения жесткости понтонов из композиционных материалов, что позволяет быстро и точно исследовать надежность любого конкретного понтона.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.142.210 (0.009 с.) |

 (7.12)
(7.12) = w0 + w1,
= w0 + w1,
 (7.15)
(7.15)

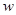 = w0 + w1,
= w0 + w1,


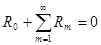 , следовательно R0=Rm=0,
, следовательно R0=Rm=0,