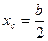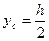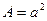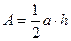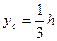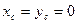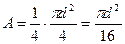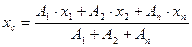Методические указания к решению задачи №3

 

К решению задачи следует приступить после изучения темы «Центр тяжести».

 

Краткие теоретические сведения

Силы притяжения отдельных частиц тела направлены приблизительно к центру Земли. Так как размеры рассматриваемых тел малы по сравнению с радиусом Земли, то эти силы можно считать параллельными. Равнодействующая этих параллельных сил, равная их сумме, есть сила тяжести тела, а центр этой системы параллельных сил, в котором приложена сила тяжести называется центром тяжести тела. Положения центров тяжести простых плоских сечений известны из геометрии.

Центры тяжести и площади некоторых простых сечений приведены ниже. Положения центра тяжести задается его координатами в прямоугольной системе координат.

Центры тяжести и площади некоторых простых сечений:

1. Прямоугольник

 

 

 

2. Квадрат

 

 

 

 

 

3. Треугольник

 

а) прямоугольный

 

 

 

 

б) равнобедренный

 

 

4. Круг

 

5. Сектор круга

 

 

 

 

Формулы для определения центра тяжести сложного составного сечения:

 

 

Последовательность решения задачи:

1. Разбить сечение на простые фигуры.

2. Рационально выбрать положение начала координат (если сечение имеет оси симметрии, то оси координат совмещают с осями симметрии).

3. Определить площади и координаты центров тяжести простых фигур, составляющих сложное сечение.

4. Определить координаты центра тяжести сложного сечения по формулам.

5. Построить центр тяжести сложного сечения.

 

Пример 3. Для заданного сложного сечения определить координаты центра тяжести и построить центр тяжести сечения.

 

Рисунок 11.

 

Решение:

1. Разбить сечение на простые фигуры:

1- прямоугольник (40×50);

2 – прямоугольный треугольник;

3 – круг.

2. Начало координат помещаем в левый нижний угол сечения. Смотри рисунок 12.

 

 

Рисунок 12

 

3. Определяем площади составных частей и координаты их центров тяжести. Все координаты указаны на рисунке 12.

Для прямоугольника, с центром тяжести в точке С₁:

 

Для прямоугольного треугольника, с центром тяжести в точке С₂:

 

Для круга, с центром в точке С₃:

 

4.Определить центр тяжести сложного сечения по формулам:

 

5. Построить центр тяжести сложного сечения по вычисленным координатам. Смотри на рисунке 12 точка «С».

 

Методические указания к решению задачи №4

 

К решению задачи следует приступать после изучения темы "Растяжение и сжатие".