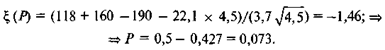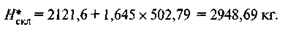Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности стохастической постановки задачи управления запасамиСодержание книги
Поиск на нашем сайте
Стохастические, или вероятностные, модели позволяют наиболее точно описать ситуации, с которыми приходится сталкиваться на практике, а значит - найти более точные решения возникающих задач. Они базируются на рассмотренных ранее трех подходах к управлению запасами, но предполагают использование более сложного математического аппарата. Кроме того, меняется один из важнейших принципов, заложенных в основу формирования моделей: если в детерминированных моделях дефицит ресурса на складе был полностью исключен, то в стохастических — его возникновение допускается с некоторой вероятностью. Вводится новый параметр управления: R0 — вероятность бездефицитной работы. Очевидно, что чем больше средств вложено в создание резервного запаса на складе, тем ближе его значение к единице, т. е. тем меньше вероятность возникновения дефицита — (1 - R0),и наоборот. Во всех трех типах стохастических моделей интенсивность потребления ресурса со склада рассматривается как величина случайная, закон распределения которой, как правило, неизвестен. (Для упрощения иногда можно считать, что это нормальный закон.) Это основное отличие такой постановки задачи управления запасами от рассмотренных ранее случаев. Учитывая то, что стохастическая постановка не меняет сути трех подходов к управлению запасами, в дальнейшем изложении обратим основное внимание на новизну математического аппарата моделей.
18.6. Управление запасами с фиксированной партией поставки (стохастический подход)
Пусть интенсивность потребления ресурса — величина случайная, распределенная нормально с параметрами МI и sI, где МI — математическое ожидание (среднее значение) и sI - среднеквадратичное отклонение случайной величины. Договором с поставщиком зафиксированы срок поставки Tпост и партия поставки nпост, причем размер партии может быть оптимизирован с помощью модели EOQ. Пусть менеджером склада установлен основной для первого способа параметр управления Hтз. Тогда неизбежно возникает вопрос: с какой вероятностью на складе не возникнет дефицита ресурса. В уже принятых обозначениях требуется найти значения Рo.Отправной точкой для дальнейших рассуждений является известная из теории вероятностей формула нахождения нормированного отклонения случайной величины от среднего:
где М*I — ожидаемое потребление ресурса за время исполнения заказа (Tпост); s*I — среднеквадратичное отклонение этой случайной величины; Р0 — вероятность того, что эта случайная величина примет любое значение, не превышающее Hтз; x(Р0) — нормированное отклонение, или квантиль, величина которого для заданного значения вероятности отыскивается по таблицам интегральной или накопленной вероятности. Из правила суммирования независимых случайных величин следует:
а из центральной предельной теоремы теории вероятностей следует, что при достаточно большом числе членов этой суммы результирующая случайная величина всегда распределена нормально независимо от законов, по которым были распределены слагаемые. Выполнив необходимые расчеты и получив значение квантиля, по таблице следует найти соответствующую ему величину Po. Это вероятность того, что к моменту получения очередной партии склад не окажется пустым. В зарубежной литературе этот параметр получил название «вероятность покрытия спроса». Для полноты картины можно определить вероятность того, что запас не будет исчерпан уже за день до поставки, или значение P1. Для получения результата выполним следующую последовательность действий:
Этот и подобные расчеты, выполненные для других сроков, могут пригодиться при установлении оптимального уровня резервного запаса. Отметим, что возникновение дефицита на складе задень, за два, за три дня до поставки — зависимые случайные величины, поэтому P1 - это часть Р0, Р2 - часть Р1и т. д. Значит, для расчета Hтз достаточно знать только Р0, и наоборот. Если полученное значение Р0 не устраивает менеджера склада, можно решить обратную задачу: по заданной им вероятности бездефицитной работы найти точку заказа. В этом случае ход решения таков:
Отсюда видно, что величина Положим, точка заказа установлена, а у менеджера склада возник другой вопрос: поместится ли на складе емкостью Н очередная поступающая партия ресурса? Переполнения склада не произойдет с вероятностью Рс, если за срок поставки будет потреблено ресурса более чем Hтз + nпост - Hскл (см. рис. 18.6). По аналогии с предыдущими рассуждениями запишем:
где Р —вероятность того, что потребление ресурса за время Tпостне превысит указанной величины. Искомая вероятность является дополнением к найденной, т. е. Рс = 1 - Р.Тогда окончательно формула примет вид:
Для решения обратной задачи следует выполнить следующие действия:
В заключение можно задаться третьим вопросом: что случится, если срок поставки будет постоянно нарушаться и в конце концов также окажется случайной величиной, распределенной нормально с параметрами МT и sТ. В этом случае вместо значения Тпоств расчетах используется Мт, а значение s*I определяется из соотношения:
Из анализа приведенной модели можно сделать следующий вывод. Вероятность бездефицитной работы склада определяет только точку заказа и величину резервного запаса. Следовательно, уменьшать партию поставки, а с ней и емкость склада можно, не снижая уровня надежности склада. Это свойство используется при расчете оптимальной партии поставки с помощью модели EOQ.
Пример 18.4 Детали изготавливаются в механическом цехе партиями по 160 шт. и поступают в соответствующий операционный накопитель сборочного конвейера. Время изготовления и доставки партии - 4,5 ч. Интенсивность потребления деталей на сборке - величина случайная, распределенная нормально с параметрами МI = 22,1 шт./ч, sI = 3,7 шт./ч. Требуется установить точку заказа и величину резервного запаса таким образом, чтобы вероятность остановки конвейера из-за отсутствия в данном накопителе деталей составляла 1 %. Определить, с какой вероятностью может произойти переполнение накопителя, если его емкость 190 деталей. Если эта вероятность больше допустимых 3%, то следует указать необходимое увеличение его емкости. Как изменится решение задачи, если срок поставки окажется случайной величиной, нормально распределенной с параметрами Мт= 4,5ч, sТ = 0,6ч? Решение Для расчета точки заказа надо знать вероятность бездефицитной работы операционного накопителя, которая является дополнением к заданной вероятности возникновения простоя, т. е.
Далее по таблице отыскивается квантиль, соответствующий этой вероятности. Обычно, используя свойство симметрии функции накопленной вероятности, в справочниках приводят лишь половину таблицы значений этой функции. Для поиска квантиля нужно знать, что в таблице тогда указывается отклонение вероятности от 0,5, и если это отклонение в большую сторону, то найденный квантиль имеет положительное значение, а если в меньшую, то отрицательное. Рассчитав соответствующий квантиль, находим точку заказа и норму резервного заноса:
Для определения вероятности переполнения накопителя сначала рассчитывается соответствующий квантиль:
Найденное значение (7,3%) превышает допустимое (3%), значит, необходимо найти новую емкость накопителя:
Если срок поставки величина случайная, пересчитывается значение s*I:
а затем с этим новым значением выполняются все остальные расчеты:
18.7. Управление запасами с фиксированным ритмом поставки (стохастический подход)
Пусть, как и в предыдущей модели, интенсивность потребления ресурса — величина случайная, распределенная нормально с параметрами МIи sI. Договором с поставщиком установлены срок и ритм поставки Тпост и Rnocт. Требуется определить емкость склада, исходя из двух условий: 1) с вероятностью Р0 должна обеспечиваться бездефицитность его работы; 2) с вероятностью Рс должно быть исключено его переполнение. Как было показано в разделе 18. 6, бездефицитность работы склада обеспечивается на интервале (Тпост + Rnocт), причем за это время должно быть потреблено ресурса не бол ее чем Н*скл (см. рис. 18.4). Здесь потребление ресурса - величина случайная, распределенная нормально с параметрами МI** и sI**,где
Формула расчета квантиля, соответствующего вероятности Р0,в этом случае имеет вид:
Тогда при известном значении Роможно найти условный максимальный запас Н*скл,выполнив следующие действия:
Реальная емкость склада может быть меньше величины Н*склна то количество ресурса, которое будет потреблено за срок поставки. Это тоже случайная величина, распределенная нормально с параметрами МI* и sI*. Для того чтобы не произошло переполнения склада, она должна принимать любые значения, не меньшие Н*скл - Hскл (см. рис. 18.4), т. е.
Тогда при известном значении Рс можно выразить Hскл через Н*скл:
Подставив в эту формулу выражение, выведенное ранее для расчета Н*скл, получим:
Таким образом, емкость склада зависит одновременно от значений обоих параметров Р0 и Рс. При задании емкости склада решается обратная задача, т. е. рассчитывается вероятность его бездефицитного функционирования или вероятность его непереполнения:
Очевидно, что одна из этих вероятностей должна быть задана, иначе обратная задача окажется неопределенной. При ее решении должно также соблюдаться условие (Hскл - МIRпост) > 0. Зная значение Н*скл, можно найти величину текущей партии поставки ресурса на склад:
Теоретически размер партии может достигать значения Н*скл, практически же на него накладывается ограничение Hскл ³ nтек, нарушение которого ведет к несостоятельности приведенных выше выкладок. Может быть также задана нижняя граница изменения названной величины - (nтек)min. В этом случае определяется вероятность Рптого, что размер текущей партии не выйдет за нее. Известно, что заказывается для очередной поставки столько ресурса, сколько его потребляется за время Rnocтотносительно уровня Н*скл(см. рис. 18.4). Тогда
На основании записанной формулы может быть решена и обратная задача.
Пример 18.5 Фирма завозит из-за границы товары для животных и реализует их в розничной сети на северо-западе России. Известен спрос на эти товары, в частности, спрос на корм для кошек составляет в среднем 624 кг в неделю (в ассортименте). Осуществляется еженедельный заказ товара у поставщиков, средний срок поставки — 2,4 нед., минимальная партия поставки корма - 400 кг, причем заказ должен быть округлен до десятков килограммов. Считается, что величина недельного спроса и срок поставки - это нормально распределенные случайные величины. Известны их среднеквадратичные отклонения: 182 кг/нед. и 0,6 нед. соответственно. В момент заказа зафиксирован остаток на складе — 212 кг, а до получения заказываемой партии ожидается поставка двух заказанных ранее партий размером 450 и 810 кг. Требуется рассчитать емкость склада, необходимую для хранения кошачьего корма, при условии, что вероятность отсутствия его в продаже может составлять не более 5%, а переполнение склада допускается с вероятностью 30%. Определить размер заказа, которыйдолжен быть сделан сегодня, найти величины резервного и среднего запасов корма на складе, а также средний срок реализации поступившей партии. Рассчитать вероятность того, что партия поставки окажется не меньше минимальной договорной величины. Решение Найдем решение сначала для фиксированного срока поставки корма Tпост = 2,4 нед. Ожидаемый расход корма за срок (Тпост + Rпост) - случайная величина с параметрами:
При допустимой вероятности дефицита корма 5%
Тогда может быть найден условный максимальный запас кошачьего корма на складе:
Емкость склада определим исходя из допустимой вероятности его переполнения 30%:
и с учетом того, что ожидаемый расход корма и среднеквадратичное отклонение его за срок поставки составят:
Проверим полученный результат, повторив расчет по сводной формуле:
Как видим, ответы практически совпали. Расчет заказываемой партии в данной ситуации будет немного отличаться от расчета по алгоритму, предложенному выше, так как он должен учитывать предстоящее получение двух заказанных ранее партий:
Принимаяво внимание необходимость округления полученной цифры и практическую нелимитированность емкости склада, установим nтек = 1210 кг. Отметим, что nтек < Hскл, значит, выполненные расчеты состоятельны. Далее определим вероятность того, что любая заказываемая в процессе управления запасом партия окажется не меньше 400 кг:
Резерв, средний запас и средний срок реализации партии определяются исходя из среднего спроса на товар:
Завершая решение задачи, проанализируем, как влияет на полученные результаты случайный характер срока поставки. Ранее был показан механизм учета такого влияния. Есть только одно отличие, отражающее принципиальную разницу между моделями с фиксированной партией и фиксированным ритмом поставки. Оно заключается в том, что резервирование запаса в первом случае производится на сроке поставки Tпост, а во втором - на интервале (Tпост + Rпост). В таком случае для разрешения наших проблем пересчитаем значение sI**:
а в качестве срока поставки будем использовать его математическое ожидание Мт. В приведенной выше формуле sT -среднеквадратичное отклонение срока поставки. Рассчитаем с учетом этого новое значение Н*скл:
Напомним, что ранее было получено значение 2673,6 кг. Очевидно, что случайный характер срока поставки оказывает существенное влияние на процесс управления запасом. Выполним пересчет параметров управления с учетом того, что ожидаемый расход корма и среднеквадратичное отклонение его при случайном сроке поставки составят:
|
||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.219.11 (0.008 с.) |

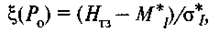


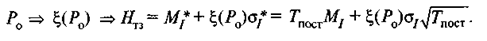
 представляет собой резервный запас, обеспечивающий с вероятностью Р0 бездефицитность работы склада. Очень важна задача нахождения его оптимального уровня. Существующие методы основаны на том, что с ростом Р0 увеличиваются затраты на создание и содержание резервного запаса ресурса, но снижаются потери ввиду его дефицита. Сложность практического применения этих методов состоит в том, как оценивать потери от дефицита ресурса и затраты на резервирование. Разные подходы к такой оценке формируют разные алгоритмы решения задачи оптимизации.
представляет собой резервный запас, обеспечивающий с вероятностью Р0 бездефицитность работы склада. Очень важна задача нахождения его оптимального уровня. Существующие методы основаны на том, что с ростом Р0 увеличиваются затраты на создание и содержание резервного запаса ресурса, но снижаются потери ввиду его дефицита. Сложность практического применения этих методов состоит в том, как оценивать потери от дефицита ресурса и затраты на резервирование. Разные подходы к такой оценке формируют разные алгоритмы решения задачи оптимизации.