
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наибольшее и наименьшее значение на отрезке.
Задача 5. Дана функция Решение. Сначала найдём производную и точки экстремума.
Точка найдём 2-ю производную.
Других экстремумов на данном отрезке нет. Производная и сама функция не существуют при
Наибольшее значение График:
Ответ. Наибольшее Задача 6. Дана функция Решение.
При Вне этого интервала В точке В точке График:
Осталось сравнить значения в точках экстремума и на концах отрезка.
Ответ. Наименьшее:
Задача 7. Найти наибольшее и наименьшее значение функции Решение. Сначала найдём экстремумы во внутренних точках.
Ответ. Наибольшее Задача 8. Найти экстремум функции 2 переменных: Решение. Найдём точку, в которой обе частные производные Получим
Тогда точка (1,3) минимум для поверхности. Замечание. Можно было выделить полный квадрат по каждой переменной и сразу получить Ответ. Точка (1,3) минимум.
Условные экстремумы. Задача 9. Дана функция Решение. Условие имеет вид
Теперь найдём их подробно, аналитическим путём. Надо функцию двух переменных свести к функции одной переменной с помощью условия, и затем искать экстремум для неё уже обычным образом. Для точки на окружности, можно задать x,y так: Тогда вместо
Переведём
итак, при При Кстати, на чертеже они тоже хорошо видны, в 1-й четверти условный максимум, в 3-й четверти условный минимум. Высота в точках условного максимума и минимума легко вычисляется, если подставить в функцию.
Замечание. Не всегда обязательно выражать переменные через t, просто здесь для окружности так было удобнее. Если в другой задаче кривая - парабола, то можно например все Ответ. Точка
Практика 24. Задача 1. Найти условный экстремум функции Решение. Поверхность Подставим условие
Значение функции в этой точке: Ответ. Точка
Задача 2. Найти наибольшее и наименьшее значение функции Решение. Сначала найдём экстремумы во внутренних точках, а затем условные экстремумы на границах квадрата, после этого сравним все значения в получившихся точках, а также в 4 углах квадрата.
Итак, осталось проверить значение функции в точках условного экстремума на границах
Наименьшее значение Чертёж этой поверхности:
Ответ. Наименьшее Задача 3. Найти отношение высоты к радиусу основания цилиндра, такое, что при фиксированном объёме получалась наименьшая площадь поверхности. Решение. Это задача на условный экстремум. Формула объёма цилиндра
Требуется, чтобы эта площадь была наименьшей. Пусть объём фиксирован и составляет 1 единицу,
Теперь найдём экстремум этой функции по
При этом Соотношение Ответ. Замечание. Для наименьшей площади поверхности диаметр цилиндра должен быть равен высоте, сбоку такой цилиндр виден именно как квадрат! Если цилиндрическая консервная банка слишком плоская, или наоборот, слишком высокая, это перерасход металла. Так что задача имеет прямое отноешние к экономике.
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.234.62 (0.035 с.) |
 . Найти её наибольшее и наименьшее значение на отрезке
. Найти её наибольшее и наименьшее значение на отрезке  .
.

 .
.



 .
.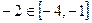 . Чтобы узнать, максимум это или минимум,
. Чтобы узнать, максимум это или минимум, =
=  =
=  .
.
 поэтому в этой точке максимум.
поэтому в этой точке максимум. , однако эта точка в рассматриваемый отрезок не входит. Теперь остаётся сравнить значения в точке экстремума и на концах отрезка.
, однако эта точка в рассматриваемый отрезок не входит. Теперь остаётся сравнить значения в точке экстремума и на концах отрезка. =
=  .
. =
= 
 =
=  .
. , наименьшее
, наименьшее  .
.
 . Найти её наибольшее и наименьшее значение на отрезке
. Найти её наибольшее и наименьшее значение на отрезке  .
. =
=  =
= вынесли множитель, который меняет знак, отдельно. Первый множитель здесь всегда больше нуля.
вынесли множитель, который меняет знак, отдельно. Первый множитель здесь всегда больше нуля. , то есть
, то есть  .
. производная положительна, там рост функции.
производная положительна, там рост функции. , убывание функции.
, убывание функции. рост сменяется убыванием, это максимум.
рост сменяется убыванием, это максимум.
 ,
,  ,
, ,
,  .
. , наибольшее:
, наибольшее:  .
. на отрезке [0,5].
на отрезке [0,5]. ,
,  только при
только при  . При этом
. При этом  , то есть там минимум. Осталось найти все значения функции в точках экстремума и в двух граничных точках и сравнить их:
, то есть там минимум. Осталось найти все значения функции в точках экстремума и в двух граничных точках и сравнить их: .
. , наименьшее
, наименьшее  .
. .
. ,
,  обращаются в 0.
обращаются в 0. . Составим матрицу из вторых производных.
. Составим матрицу из вторых производных. =
=  она соответствует положительно-определённой квадратичной форме
она соответствует положительно-определённой квадратичной форме  . Проще говоря, в каждом из двух перпендикулярных сечений поверхности такая кривая, что 2-я производная больше нуля, то есть по каждому сечению минимум.
. Проще говоря, в каждом из двух перпендикулярных сечений поверхности такая кривая, что 2-я производная больше нуля, то есть по каждому сечению минимум. тогда было бы видно, что в любой точке значение больше нуля, а в то же время
тогда было бы видно, что в любой точке значение больше нуля, а в то же время  .
. . Найти условные экстремумы этой функции на окружности
. Найти условные экстремумы этой функции на окружности  .
. . Наклонная плоскость
. Наклонная плоскость  наклонена в сторону биссектрисы первой четверти. Окружность под плоскостью проецируется наверх, и там получается эллипс, и видно, что у него есть точки максимальной и минимальной высоты.
наклонена в сторону биссектрисы первой четверти. Окружность под плоскостью проецируется наверх, и там получается эллипс, и видно, что у него есть точки максимальной и минимальной высоты.
 .
. можно получить в итоге
можно получить в итоге  =
=  .
. .
. .
.  при
при  , то есть
, то есть  и
и  .
. . Тогда
. Тогда  , там условный максимум.
, там условный максимум.  , там условный минимум.
, там условный минимум.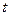 обратно в декартовы координаты
обратно в декартовы координаты  .
. .
. .
. .
. =
=  .
. =
=  .
. заменить на
заменить на  , и тоже
, и тоже  .
. при условии, что
при условии, что  .
. это наклонная плоскость. Ни одна точка на ней не является точкой экстремума, ведь в её окрестности есть другие точки как выше, так и ниже. Однако если сузить область определения, то есть рассматривать не всю плоскость, а только параболу, над параболой есть точка минимальной высоты.
это наклонная плоскость. Ни одна точка на ней не является точкой экстремума, ведь в её окрестности есть другие точки как выше, так и ниже. Однако если сузить область определения, то есть рассматривать не всю плоскость, а только параболу, над параболой есть точка минимальной высоты. , свели к функции одной переменной, и для неё уже ищем обычный экстремум.
, свели к функции одной переменной, и для неё уже ищем обычный экстремум.

 .
. , т.е. минимум.
, т.е. минимум. .
. условный минимум.
условный минимум. в области
в области  .
. никогда не обращается в (0,0) из-за первой координаты. Экстремумов во внутренних точках нет. Теперь ищем условные экстремумы на границах квадрата.
никогда не обращается в (0,0) из-за первой координаты. Экстремумов во внутренних точках нет. Теперь ищем условные экстремумы на границах квадрата. .
.  ,
,  , экстремум при
, экстремум при  , то есть в точке
, то есть в точке  , это условный максимум, т.к.
, это условный максимум, т.к.  .
. .
.  ,
,  , это условный максимум, т.к.
, это условный максимум, т.к.  .
.  ,
,  , экстремумов нет.
, экстремумов нет. .
.  ,
,  .
.




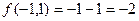
 , наибольшее 1.
, наибольшее 1.
 наибольшее
наибольшее  . Полная площадь поверхности это сумма площади боковой поверхности и площадей 2 кругов, то есть верхней и нижней грани цилиндра. Она вычисляется по формуле:
. Полная площадь поверхности это сумма площади боковой поверхности и площадей 2 кругов, то есть верхней и нижней грани цилиндра. Она вычисляется по формуле: =
=  .
. . Тогда
. Тогда  . Таким образом, мы можем в функции
. Таким образом, мы можем в функции  одну из двух переменных выразить через другую, то есть получится функция одной переменной.
одну из двух переменных выразить через другую, то есть получится функция одной переменной. =
=  =
=  .
. .
. =
=  . Найдём, когда производная равна 0.
. Найдём, когда производная равна 0.


 .
. =
=  .
. =
=  =
=  =
=  =
= 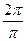 = 2.
= 2. .
.


