
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость графика и асимптоты. ⇐ ПредыдущаяСтр 5 из 5
Задача 4. Найти интервалы выпуклости вверх и выпуклости вниз и асимптоты графика функции Решение. Сначала, очевидно, надо найти первую производную.
Первая производная положительна, она может обратиться в 0 лишь при Теперь найдём 2-ю производную.
Сократим по крайней мере на одну степень выражения
= 1) 2) Теперь сопоставим эти интервалы, вот на схеме жёлтым показано, на каком интервале то или иное выражение положительно, а зелёным - отрицательно:
Итак, На этих интервалах график выпуклый вниз.
На этих интервалах график выпуклый вверх. Точки перегиба Поиск асимптот.
Видно, что сначала график отходит от асимптоты, в это время выпуклый вниз. Потом после Примечание. Сравнение с реальной ситуацией - машина, которая съехала с дороги, потом возвращается но проскочила мимо, потом снова начинает приближаться, но уже с другой стороны и плавно. Задача 5. Найти асимптоты графика функции Решение. Во-первых, при
Ответ. Вертикальная
Задача 6. Найти асимптоты графика функции Решение. Область определения:
здесь умножили на сопряжённое, как в таких пределах делали раньше.
Итак, Ответ. Две односторонние асимптоты График (асимптоты показаны зелёным цветом).
Задача 7. Найти асимптоты графика функции Решение. Функция не является чётной, поэтому здесь придётся при
Итак, На левой полуплоскости:
=
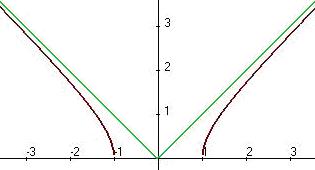
Ответ. На правой полуплоскости наклонная асимптота на левой горизонтальная асимптота Вот график этой функции:
Задача 8. (Производная функции, заданной неявно). Решение. Во-первых, проверим, что эта точка принадлежит кривой.
Ответ.
Практика 25.
Задача 1. Дано:
Решение. 1 способ. Сведём к функции от
2 способ. По формуле полной производной: =
Ответ.
Задача 2. Вывести формулу Решение. Объединим первые 2 слагаемых в один условный множитель, а третье пусть будет вторым множителем. После этого применим известную формулу, доказанную для 2 множителей.
выражению
Задача 3. Найти производную для
Решение. По формуле из прошлой задачи, для 3 множителей:
Ответ.
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.181.231 (0.033 с.) |
 .
. =
=  =
=  .
. . Так как она нигде не отрицательна (ведь все степени чётные) то интервал роста не сменяется интервалом убывания, а снова продолжается рост. Таким образом, мы установили, что экстремумов нет, функция монотонно возрастает.
. Так как она нигде не отрицательна (ведь все степени чётные) то интервал роста не сменяется интервалом убывания, а снова продолжается рост. Таким образом, мы установили, что экстремумов нет, функция монотонно возрастает. =
= 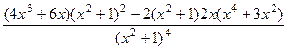
 .
. =
=  =
= =
=  выделили множитель, который заведомо больше 0, а также там видим 2 множителя, которые могут менять знак. Когда они одного знака, оба плюс или минус, тогда вторая производная больше 0, а когда разного знака, тогда меньше 0.
выделили множитель, который заведомо больше 0, а также там видим 2 множителя, которые могут менять знак. Когда они одного знака, оба плюс или минус, тогда вторая производная больше 0, а когда разного знака, тогда меньше 0. на
на 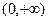 ,
,  на
на 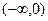 .
.


 .
.
 , если
, если  и
и 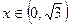 .
. и
и  .
.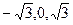 .
. =
=  = 1.
= 1. =
=  =
=  =
= . Асимптота
. Асимптота  . Вот чертёж:
. Вот чертёж:
 начинает возвращаться, в это время выпуклость вверх. Пересекает её, начинается торможение, в это время выпуклость вниз. А потом до бесконечности приближается к асимптоте, в это время выпуклость вверх.
начинает возвращаться, в это время выпуклость вверх. Пересекает её, начинается торможение, в это время выпуклость вниз. А потом до бесконечности приближается к асимптоте, в это время выпуклость вверх. .
. знаменталь обращается в 0, здесь разрыв 2 рода. То есть, вертикальная прямая
знаменталь обращается в 0, здесь разрыв 2 рода. То есть, вертикальная прямая  =
=  = 2. Причём этот результат не зависит от того, предел при
= 2. Причём этот результат не зависит от того, предел при  или
или  , ведь обе старшие степени чётные. Нашли
, ведь обе старшие степени чётные. Нашли  , т.е. есть наклонная асимптота типа
, т.е. есть наклонная асимптота типа  . теперь найдём
. теперь найдём  .
. =
=  =
= =
=  =
=  . Итак,
. Итак,  и опять же, это независимо от
и опять же, это независимо от  это двусторонняя асимптота.
это двусторонняя асимптота. . График:
. График:
 .
. . Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при
. Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при  , поэтому и горизонтальных асимптот нет, так что ищем только наклонные. Функция чётная, поэтому можем искать только при
, поэтому и горизонтальных асимптот нет, так что ищем только наклонные. Функция чётная, поэтому можем искать только при 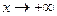 на правой полуплоскости, а на левой график симметричен, так что если
на правой полуплоскости, а на левой график симметричен, так что если  будет асимптотой на правой полуплоскости, то
будет асимптотой на правой полуплоскости, то на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.
на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная. =
=  =
=  = 1.
= 1. =
=  =
= 
 =
=  =
= 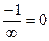 .
. ,
, 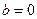 , на правой полуплоскости асимптота
, на правой полуплоскости асимптота  .
.
 .
. =
=  =
=  =
=  .
. =
=  =
= =
=  =
=  = 0.
= 0. .
. =
=  =
= =
=  .
. =
=  =
= 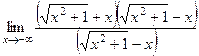
 =
=  но так как
но так как  отрицательно то
отрицательно то . Итак, на левой полуплоскости
. Итак, на левой полуплоскости 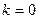 ,
,  .
.
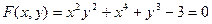 . Найти производную в точке (1,1).
. Найти производную в точке (1,1). , да, принадлежит. Ищем производную:
, да, принадлежит. Ищем производную: =
= 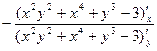 =
=  =
=  =
=  .
. . Точка движется по прямой:
. Точка движется по прямой: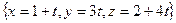 . Вычислить
. Вычислить  с помощью формулы полной производной и без её использования.
с помощью формулы полной производной и без её использования.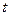 и вычислим для неё обычную производную.
и вычислим для неё обычную производную.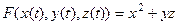 =
= 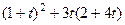 =
=  =
=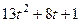 ,
,  =
=  .
. =
=  =
=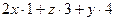 а теперь уже в этом выражении выразим
а теперь уже в этом выражении выразим  через
через  =
=  =
=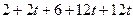 =
=  .
. =
=  , что и приводит к
, что и приводит к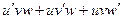 .
. .
. =
=  =
= .
.


