
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Серия задач, где разложение получается с помощью геометрической прогрессии.
Задача 10. Разложить в степенной ряд Решение. Представим
Ответ. Задача 11. Разложить в степенной ряд Решение. Здесь константа не равна 1, тогда можно вынести константу за скобки, и тогда получится Итак, Ответ. Задача 12. Разложить в степенной ряд Решение. Здесь разложение в окрестности другой точки, а не 0, в этом случае надо изначально сделать арифметическое преобразование, чтобы отделить слагаемое вида
Затем вынесем за скобку констенту 4, чтобы в знаменателе выражение начиналось с 1, т.е. чтобы присутствовала структура типа А уже после этого, в качестве знаменателя прогрессии получается
Это верно в такой области: Ответ. Приложения формулы Тейлора. Нахождение производных высокого порядка. Допустим, нужно вычислить производную 10 порядка в точке 0 для функции, содержащей произведение, например
Задача 13. Найти Решение. Итак, коэффициент при 10-й степени равен
Ответ.
Практика 23 (16 декабря у обеих групп). Экстремумы. Задача 1. Найти интервалы монотонности и экстремумы функции Решение. Найдём производную. Ищем корни этого многочлена. Для определения интервалов монотонности надо найти знак производной на интервалах
1) 2)
3) В точке 2 рост сменяется убыванием, это максимум. В точке 3 убывание сменяется остом, это минимум. Кстати, тип экстремума можно найти и с помощью 2 производной: Выясним знак 2-й производной в этих точках.
Ответ.
Задача 2. Найти экстремумы функции Решение. Производная: Чтобы определить, где максимум, а где минимум, выясним знак 2-й производной в этих же точках.
Ответ.
Задача 3. Найти интервалы монотонности и экстремумы функции Решение.
От знаменателя знак не зависит, знаменатель тут всегда строго больше 0. Поэтому всё зависит только от знака числителя. Выделим множитель, который может менять свой знак: На интервалах На интервале В точке В точке Кстати, в этом примере с помощью интервалов узнать экстремумы проще, чем с помощью 2-й производной, ведь пришлось бы считать поизводную от дроби Для построения графика можем найти высоту в точках максимума и минимума: Вот как выглядит график:
Ответ.
Задача 4. Найти интервалы монотонности и экстремумы функции Решение. Сначала найдём корни выражения под знаком модуля, чтобы понять, какая часть параболы отражается вверх.
Тогда знак меняется на интервале График:
Производная: Производная разрывна при Выбирая целочисленную точку на каждом интервале, найдём знак производной на этом интервале.
Таким образом, Ответ.
|
||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.251.68 (0.029 с.) |
 в окрестности
в окрестности 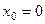 .
. , и тогда знаменатель прогрессии будет
, и тогда знаменатель прогрессии будет  . Эта функция представляет собой сумму бесконечной геометрической прогрессии, записанную в свёрнутом виде, т.е. мы по формуле должны развернуть её обратно в сумму.
. Эта функция представляет собой сумму бесконечной геометрической прогрессии, записанную в свёрнутом виде, т.е. мы по формуле должны развернуть её обратно в сумму. .
. .
. в окрестности
в окрестности  . Мы можем пользоваться этой формулой при условии, что
. Мы можем пользоваться этой формулой при условии, что  , то есть
, то есть  .
.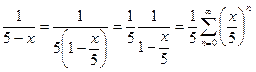 =
= 
 =
=  .
. .
.
 . Итак,
. Итак,  .
. и тогда, при условии, что
и тогда, при условии, что  , получим
, получим  .
. , т.е.
, т.е. 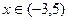 .
. . Если просто считать производные до 10 порядка, и лишь затем фиксировать число, то на каждом шаге по формуле
. Если просто считать производные до 10 порядка, и лишь затем фиксировать число, то на каждом шаге по формуле 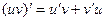 происходит удвоение количества слагаемых. Таким образом, их будет до 1024. Некоторые из них обнуляются в процессе, так как понижается степень, так что в реальности меньше, но всё равно, это очень трудоёмкая работа, вычислить 10 производную для такого типа функции. Вместо этого, мы можем выбрать коэффициент при 10 степени из разложения в ряд Тейлора.
происходит удвоение количества слагаемых. Таким образом, их будет до 1024. Некоторые из них обнуляются в процессе, так как понижается степень, так что в реальности меньше, но всё равно, это очень трудоёмкая работа, вычислить 10 производную для такого типа функции. Вместо этого, мы можем выбрать коэффициент при 10 степени из разложения в ряд Тейлора.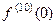 для функции
для функции  =
= 
 . Теоретически же этот коэффициент должен быть
. Теоретически же этот коэффициент должен быть  . Приравняем эти значения.
. Приравняем эти значения. =
=  =
=  .
.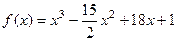 .
. .
.


 ,
,  , корни 2 и 3.
, корни 2 и 3. ,
, 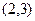 и
и  . Знак производной может меняться только в точках 2 и 3, на интервалах он остаётся неизменным. Надо выбрать какую-нибудь наиболее удобную для вычислений точку на интервале, желательно с целой абсциссой.
. Знак производной может меняться только в точках 2 и 3, на интервалах он остаётся неизменным. Надо выбрать какую-нибудь наиболее удобную для вычислений точку на интервале, желательно с целой абсциссой. ,
,  , на этом интервале монотонный рост.
, на этом интервале монотонный рост. здесь очевидно, целое выбрать не получится.
здесь очевидно, целое выбрать не получится. =
=  =
=  =
=  , на этом интервале монотонное убывание.
, на этом интервале монотонное убывание. ,
,  =
=  =
=  , здесь монотонный рост.
, здесь монотонный рост. .
.
 максимум.
максимум. .
.
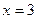 минимум.
минимум. .
. и разность между ординатами максимума и минимума.
и разность между ординатами максимума и минимума. . Стационарные точки (где производная = 0)
. Стационарные точки (где производная = 0)  и
и  .
.
 .
.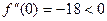 , точка
, точка  точка
точка  ,
,  .
.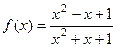 .
. =
= =
= =
=  .
. . Корни
. Корни  .
. и
и 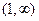 :
:  , рост.
, рост. :
: 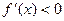 убывание.
убывание. рост сменяется убыванием, это максимум.
рост сменяется убыванием, это максимум. убывание сменяется ростом, это минимум.
убывание сменяется ростом, это минимум. ,
,  .
.
 .
. ,
,  ,
,  , корни
, корни  и 3.
и 3. , то есть функцию можно записать в виде:
, то есть функцию можно записать в виде:  .
.
 .
. и обращается в 0 при
и обращается в 0 при  убывание на
убывание на 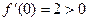 рост на
рост на 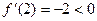 убывание на
убывание на  .
. рост на
рост на  .
.


