
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ребристо-кольцевые и сетчатые купола. Конструирование куполов, особ-и расчета.Содержание книги
Поиск на нашем сайте
В ребристо-кольцевых схемах купольных покрытий в общую работу каркаса купола включены непрерывные кольцевые прогоны, которые пересекают меридианные ребра и работают не только на местный изгиб, но и воспринимают растягивающие кольцевые усилия, являясь ярусными затяжками. Сечения такого купола в плоскости кольцевых прогонов не имеют свободных горизонтальных перемещений. Высота поперечного сечения ребер благодаря участию в общей работе купола кольцевых прогонов уменьшается до 1/100—1/150 диаметра купола. Ребра с кольцевыми прогонами соединяются, как правило, шарнирно. Кольцевые прогоны и ребра чаще всего изготовляют из клееной древесины, но могут быть и клеефанерными. Верхнее и нижнее кольца, а также скатные и поперечные связи между ребрами, устраивают как и в ребристых куполах. Внешний вид ребристо-кольцевого купола аналогичен ребристому куполу. При осесимметричной нагрузке расчет купола можно вести, расчленяя его на плоские арки с условными затяжками-кольцами, каждая из которых полностью воспринимает приходящуюся на ее долю нагрузку, так как силы взаимодействия между арками в ключе равны нулю. Площадь сечения условных затяжек определяют по формуле
. Пример многогранного купола на рис.IX. 35, а. Сетчатые купола рассчитывают по безмоментной теории как сплошные осесимметричные оболочки). Усилия в стержнях купола определяют умножением меридиональных Т1 и кольцевых Т2 усилий на соответствующие расстояния между стержнями в рассматриваемых сечениях купола, и проектировании этих усилий на направления стержней (рис. IX.35, б). При ячейке в виде равностороннего треугольника усилия в стержнях:
Местная потеря устойчивости сетчатого купола состоит в явлении продавливания узла к центру сферы '(рис. 1Х.35,в). Для расчета на местную устойчивость необходимо проверить на продольный изгиб стержень узла при расчетной длине, равной
где rc — радиус инерции сечения стержня; I — длина стержня; h — величина превышения вершины узла пирамиды над примыкающими к нему соседними узлами. Чтобы избежать общей потери устойчивости сетчатой оболочки необходимо, чтобы равномерное радиальное давление на сферический купол не превышало критического. gкр=1.6*Е*F*rc/(l * r^2) где Е, F, rc,l —модуль упругости, площадь, радиус инерции и длина стержня; r — радиус сферы.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 801; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.152 (0.005 с.) |

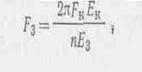
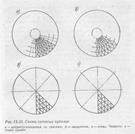 где п— количество ребер в куполе; Fк, Ек,— площадь и модуль упругости кольца; Fз, Ез — площадь и модуль упругости условной затяжки. Усилия в затяжках проще всего вычислить методом сил. В ребристо-кольцевом куполе устанавливаются решетчатые связи в каждой четырехугольной ячейки. Диагональные связи участвуют в общей работе купола, что приводит к уменьшению усилий в ребрах и кольцах. Именно по такой конструктивной схеме чаще всего прое-ют купола большого диаметра. В рамном куполе изгибающие моменты в ребрах примерно на15% меньше, чем в ребристо-кольцевом с шарнирным присоединением колец к рёбрам. Сетчатые купола —это многогранники, вписанные чаще всего в сферическую поверхность вращения. Сетка обычно образуется из треугольников, трапеций, ромбов пятиугольников, шестиугольников и других фигур. Стержни решетки в узлах сетчатых куполов соединяются шарнирно. Сетчатый купол является распорной системой, который воспринимается нижним опорным кольцом. Они отличаются легкостью, четкостью и декоративностью рисунка конструктивных элементов. Различают два метода построения сетчатых поверхностей. Для пологих куполов хар-ен первый метод: 1) ребристо-кольцевая со связями (рис. IX. 33,а) 2)звёздчатая схема (рис. IX. 33,б) 3) схема Чивитта (рис. IX. 33,в) 4) схема ромба (рис. IX. 33,г)
где п— количество ребер в куполе; Fк, Ек,— площадь и модуль упругости кольца; Fз, Ез — площадь и модуль упругости условной затяжки. Усилия в затяжках проще всего вычислить методом сил. В ребристо-кольцевом куполе устанавливаются решетчатые связи в каждой четырехугольной ячейки. Диагональные связи участвуют в общей работе купола, что приводит к уменьшению усилий в ребрах и кольцах. Именно по такой конструктивной схеме чаще всего прое-ют купола большого диаметра. В рамном куполе изгибающие моменты в ребрах примерно на15% меньше, чем в ребристо-кольцевом с шарнирным присоединением колец к рёбрам. Сетчатые купола —это многогранники, вписанные чаще всего в сферическую поверхность вращения. Сетка обычно образуется из треугольников, трапеций, ромбов пятиугольников, шестиугольников и других фигур. Стержни решетки в узлах сетчатых куполов соединяются шарнирно. Сетчатый купол является распорной системой, который воспринимается нижним опорным кольцом. Они отличаются легкостью, четкостью и декоративностью рисунка конструктивных элементов. Различают два метода построения сетчатых поверхностей. Для пологих куполов хар-ен первый метод: 1) ребристо-кольцевая со связями (рис. IX. 33,а) 2)звёздчатая схема (рис. IX. 33,б) 3) схема Чивитта (рис. IX. 33,в) 4) схема ромба (рис. IX. 33,г)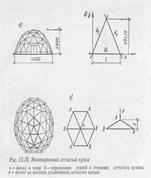 Второй - для подъемистых сферических куполов и основан на последовательном членении вписанных в сферу правильных многогранников—додекаэдра (двенадцатигранник) и косаэдра (двадцатигранник).
Второй - для подъемистых сферических куполов и основан на последовательном членении вписанных в сферу правильных многогранников—додекаэдра (двенадцатигранник) и косаэдра (двадцатигранник). Кроме N1,N2,N3 в стержнях могут возникать изгибающие моменты от местной нагрузки, которые необходимо учитывать при расчете стержней на внецентренное сжатие.
Кроме N1,N2,N3 в стержнях могут возникать изгибающие моменты от местной нагрузки, которые необходимо учитывать при расчете стержней на внецентренное сжатие.



