
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системи лінійних рівнянь та методи їх розв’язування.Содержание книги
Поиск на нашем сайте
Розв ’ язати системи а) методом Крамера, б) матричним методом, в) методом Гаусса:
Практичне заняття №4.
Елементи векторної алгебри. 1. Задано координати точок A(2; 1; -4), В(1; 3; 5), С(7; 2; 3) та D(8; 0; -6). Довести, що АВСD – паралелограм та знайти довжини його сторін та величини кутів. 2. В трикутнику АВС знайти довжину медіани, проведеної з вершини С, та кут між цією медіаною та сторонами СА та СВ. Знайти проекцію сторони СА на сторону СВ та проекцію сторони СВ на сторону АС. 3. Довести, що у чотирикутника АВСD діагоналі перпендикулярні, якщо координати вершин наступні: А(1; 2; 3), В(7; 3; 2), С(-3; 0; 6) та D(9; 2; 4). 4. Задано координати точок A(2; 3; 4), В(-1; 0; 6), С(-2; 2; 3) та D(-3; 3; 0). Знайти: площу трикутника АВС та паралелограма, побудованого на векторах об’єм піраміди АВСD та об’єм паралелепіпеда, побудованого на векторах висоту трикутника АВС, проведену з вершини А; висоту піраміди АВСD, проведену з вершини D.
Практичне заняття №5.
Рівняння прямої на площині. В трикутнику АВС задано координати вершин: A(-1; -2), В(4; -1), С(3; 5). Скласти рівняння: а) всіх сторін трикутника; б) всіх медіан трикутника; в) всіх висот трикутника; г) всіх прямих, що проведені через вершини трикутника паралельно протилежним сторонам; Знайти величини всіх кутів трикутника.
Практичне заняття №6.
Лінії другого порядку. Звести лінії другого порядку до канонічного вигляду; знайти координати центрів, вершин, фокусів; побудувати.
Практичне заняття №7. Аналітична геометрія у просторі.
1) Скласти рівняння площини, що проходить через три точки 2) Скласти рівняння площини, що проходить через точку 3) Скласти рівняння площини, що проходить через точку 4) Скласти рівняння площини, що проходить через точки 5) Скласти рівняння площини, що проходить через точку 6) Через точку а) р:
б) р: в) р: 7) Знайти кут між прямими 8) Скласти рівняння площини, що проходить через пряму 9) Знайти відстань між точкою 10) Знайти точку перетину площини
Практичне заняття № 8.
Функції однієї змінної. Способи задання та властивості функцій. Знайти область існування функцій:
Практичне заняття №9.
Елементи теорії границь. Границі числових послідовностей та функцій. Обчислити границі:
Практичне заняття № 10. Методи обчислення границь функцій.
Обчислити границі:
Практичне заняття № 11. Неперервність і точки розриву функції. Наступні функції дослідити на неперервність, схематично побудувати графіки.
Практичне заняття №12.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.01 с.) |






 ;
; ;
;
 .
.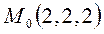 паралельно площині
паралельно площині 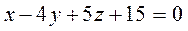 .
.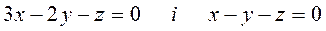 .
. перпендикулярно площині
перпендикулярно площині  .
. паралельно векторам
паралельно векторам  .
. провести пряму, яка паралельна заданій прямій р.
провести пряму, яка паралельна заданій прямій р. ;
; ;
; ;
;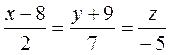 та
та  та точку
та точку  .
.
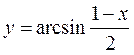

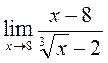





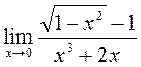
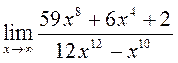




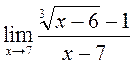


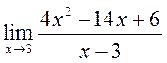



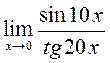









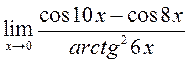





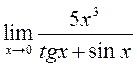
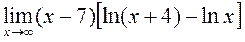



 3)
3) 



