
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение приведённых геометрических характеристик поперечного сечения плитыСодержание книги
Поиск на нашем сайте
Приведённая площадь сечения: Fпр=bрасч∙δф+bр.пр.∙hр =1,332∙0,008+0,311∙0,144=5,5∙10-2 м². Приведённый статический момент сечения относительно нижней плоскости плиты: Sпр=bрасч Координата центра тяжести сечения плиты относительно нижней плоскости:
hп - y0 = 0,152– 0,087 = 0,065 м Площади и координаты центров тяжести элементов поперечного сечения плиты относительно нейтральной оси: - фанерной обшивки: Fф.=bрасч.∙δф.в .=1,332 ∙0,008=106,56 ∙10-4 м² yф.= hп - y0 - = 0,152 – 0,087 – - продольных рёбер: Fр.пр.=bр.пр.∙hр =0,311∙0,144=447,84∙10-4 м²; yр.= y0 - – δф.н.= 0,087– Приведённые собственные моменты инерции элементов поперечного сечения плиты: - фанерноей обшивки: Iф.= - продольных рёбер: Iр.пр.= Приведённый момент инерции сечения плиты: Iпр.=Iф.+Iр.пр.+Fф.∙y²ф.+Fр.пр.∙y²р .= 5,683∙10-8 + 0,774∙10-4 + 106,56∙10-4 ∙ 0,061² + +447,84∙10-4∙0,015² = 1,27∙10-4 м4. Приведённый момент сопротивления сечения плиты:
Приведённый момент сопротивления сечения плиты ребер:
Статический момент верхней обшивки относительно нейтральной оси: Sф.пр.=Fф.∙yф. =106,56∙10-4∙0,061 =6,5∙10-4 м3. Приведённый статический момент верхней сдвигаемой части сечения плиты относительно нейтральной оси: Sx,пр = bр.пр∙ Подсчёт нагрузок на плиту Подсчёт нагрузок на плиту производится в соответствии с указаниями [2]. Нормативный вес конструкций или отдельных конструктивных элементов плиты приходящейся на единицу покрытия определяется по формулам: gсв= где bn – ширина плиты; ln – длина плиты; V – объём конструктивного элемента или сумма объемов однотипных элементов; ρ – плотность материала элемента; ρs – поверхностная плотность материала; δф – толщина фанерных обшивок. Нормативное значение снеговой нагрузки S0 на покрытие определяется по формуле: S0=0,7∙се∙сt∙Sg∙μ где Sg =3200 Па–вес снегового покрова на 1 м2 горизонтальной поверхности по п.10.2 [2]; се – коэффициент, учитывающий снос снега с покрытий зданий под действием ветра по п.10.5 [2]; сt =1 – термический коэффициент по п.10.10 [2]; μ =1 – коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, по табл. Г1 [2];
где ν– средняя скорость ветра за три наиболее холодные месяца; k – принимается по табл. 11.2 [2]; b – ширина покрытия, принимаемая не более 100 м.
S0 =0,7∙0,69∙1∙2400∙1 = 1159,2 Па Расчётное значение снеговой нагрузки определяется путём умножения нормативной нагрузки на коэффициент надежности по нагрузке, по п.10.12 [2]. S = S0∙γf = 1159,2∙1,4 = 1622,88 Па Расчетная нагрузка от веса конструкций определяется путем умножения нормативной нагрузки на коэффициент надежности по нагрузке по п.2.2 [2]. Линейная нагрузка на плиту в Па определяется путём умножения нагрузки на покрытие в Па на ширину плиты bn =1,5 м. Расчёт нагрузок на плиту приведён в таблице 1.4. Таблица 1.4 - Подсчёт нагрузок на плиту
Расчет плиты на прочность Расчётные значения внутренних усилий в плите определяем как в простой балке двутаврового сечения (рис. 1.2.) с пролётом равным lрасч =3.93 м нагруженной линейной равномерно-распределённой нагрузкой q =3500Н/м:
Фанерную обшивку проверяем на устойчивость в соответствии с п. 6.28 [1].
Коэффициент φф находим в зависимости от отношения:
Фанерная обшивку плиты проверяем на местный изгиб от сосредоточенного груза Р=1000 Н с коэффициентом перегрузки n=1,2 при ширине расчётной полосы b′ф.в.=1,0 м по схеме приведённой на рисунке 1.5. M1=
Рисунок 1.5 – Расчетная схема верхней обшивки на местный изгиб Проверяем прочность продольных ребер при изгибе плиты:
В соответствии с п.6.29 [1] рёбра, по нейтральному слою, и клеевой шов между рёбрами и фанерной обшивкой проверяются на скалывание при изгибе. - Рёбра по нейтральному слою:
bрасч=nр∙bр=5∙0,056=0,28 м. - Клеевой шов между рёбрами и обшивкой:
Как видно из выполненного расчёта принятые размеры и конструкция элементов плиты покрытия удовлетворяют требованиям прочности. Расчёт плиты на жёсткость В соответствии с п.п. 6.35 и 6.36 [1] прогиб плиты определяется с учётом деформаций сдвига по формуле:
k=1 – так как высота плиты постоянна; с=(45,3–6,9∙β)∙γ=(45,3 - 6,9∙1)∙0,238=9,1392; β=1 – так как высота панели постоянна; γ= Коэффициенты k, с, β, γ определяются по таблице E.3 приложения E [1] как для балки двутаврового сечения, постоянной высоты, с шарнирными опорами и линейной равномерно-распределённой нагрузкой. Относительный прогиб плиты равен:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.126.124 (0.006 с.) |

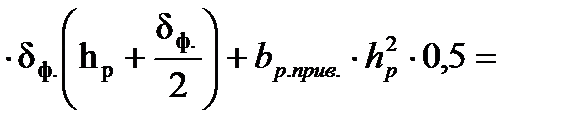
 4,8∙10-3 м3.
4,8∙10-3 м3. 0,087 м;
0,087 м;
 = 0,061 м.
= 0,061 м. = 0,015м.
= 0,015м.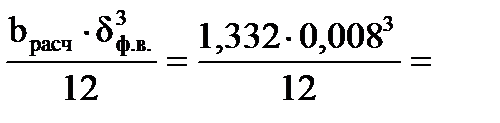 5,683∙10-8 м4
5,683∙10-8 м4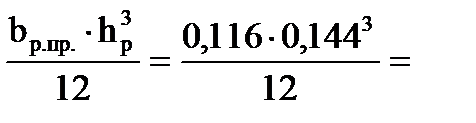 0,774∙10-4 м4
0,774∙10-4 м4 1,95∙10-3 м3.
1,95∙10-3 м3. 1,46 ∙10-3 м3.
1,46 ∙10-3 м3. = 0,311∙
= 0,311∙  =1,18∙10-3 м3.
=1,18∙10-3 м3.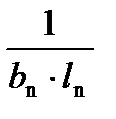 ∙V∙ρ∙g или gсв=ρs ∙ g или gсв=δф∙ρ∙g,
∙V∙ρ∙g или gсв=ρs ∙ g или gсв=δф∙ρ∙g,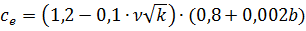
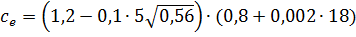 =0,69
=0,69 ∙ bр∙hp∙lp∙np∙ρр∙g= =
∙ bр∙hp∙lp∙np∙ρр∙g= =  ∙0,056∙0,144∙6∙5∙500∙9,81
∙0,056∙0,144∙6∙5∙500∙9,81
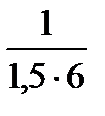 ∙0,056∙0,144∙0,3∙8∙500∙9,81
∙0,056∙0,144∙0,3∙8∙500∙9,81
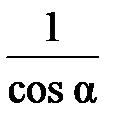 ;α =22о
;α =22о
 6758 Н∙м;
6758 Н∙м;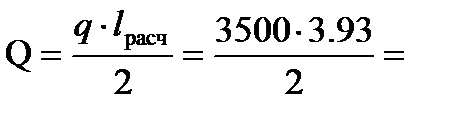 6878 Н.
6878 Н.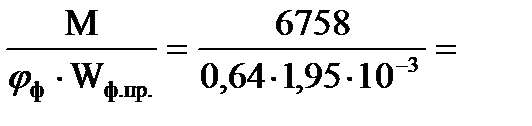 4,8∙106 Па=5,62 МПа < Rфс∙mс=12∙0,9=10,8 МПа.
4,8∙106 Па=5,62 МПа < Rфс∙mс=12∙0,9=10,8 МПа.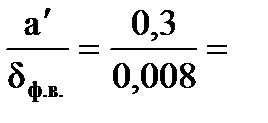 37,5 < 50, тогда
37,5 < 50, тогда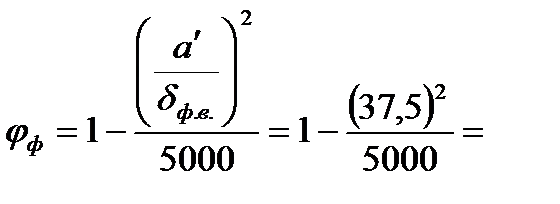 0,719
0,719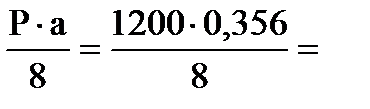 53,4 Н∙м;
53,4 Н∙м;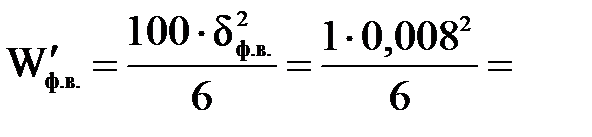 10,7∙10-6 м3;
10,7∙10-6 м3;
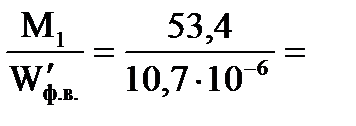 4,99∙106 Па=4,99 МПа < Rфи∙mп ∙mн=6,5∙0,9∙1,2=7,02 МПа.
4,99∙106 Па=4,99 МПа < Rфи∙mп ∙mн=6,5∙0,9∙1,2=7,02 МПа.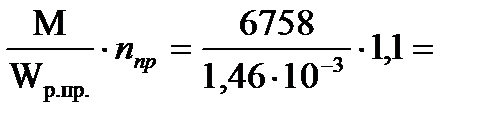 5,14∙106 Па=5,14 МПа < Rи∙mп=13∙0,9=11,7 МПа.
5,14∙106 Па=5,14 МПа < Rи∙mп=13∙0,9=11,7 МПа.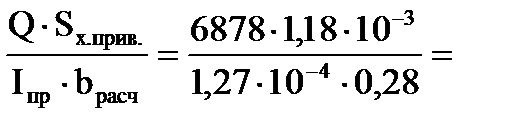 0,23∙106 Па=0,23 МПа < Rск∙mп =1,6∙0,9=1,17 МПа
0,23∙106 Па=0,23 МПа < Rск∙mп =1,6∙0,9=1,17 МПа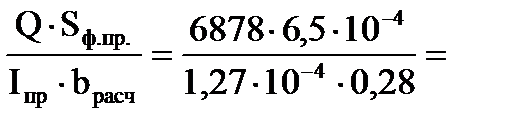 0,13∙106 Па=0,13 МПа < Rф.ск∙mп =0,8∙0,9=0,72 МПа
0,13∙106 Па=0,13 МПа < Rф.ск∙mп =0,8∙0,9=0,72 МПа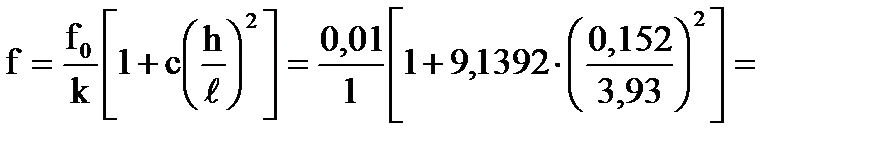 0,0101 м=10,1 мм;
0,0101 м=10,1 мм;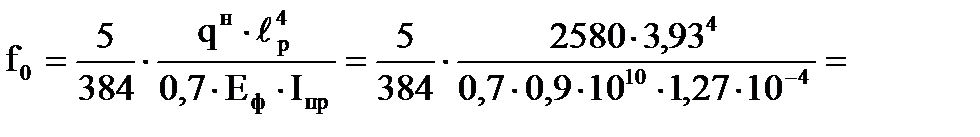 0,01 м=10 мм;
0,01 м=10 мм;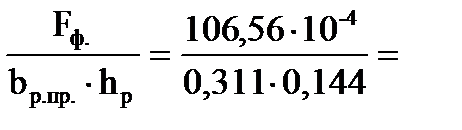 0,238.
0,238. =
= 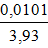 =
= 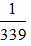 <
< 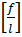 =
= 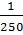 в соответствии с п. 6.34 [1], плита покрытия удовлетворяет требованиям жёсткости.
в соответствии с п. 6.34 [1], плита покрытия удовлетворяет требованиям жёсткости.


