
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 4 «оптимізаційні задачі управління економічними системами на основі застосування теорії мереж»Содержание книги
Поиск на нашем сайте Анотація Основні поняття теорії графів. Алгоритм побудови мінімального покриваючого дерева. Алгоритми визначення найкоротшого шляху (Дейкстри та Флойда) між вузлами мережі. Задача про максимальний потік.
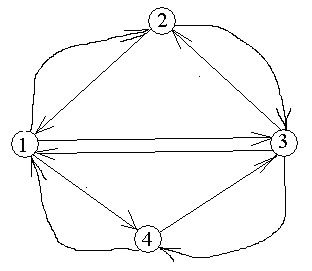
4.1 Основні поняття теорії графів Графом G = (X, А) називається пара об’єктів X = { x1, x2., xn } і А = { a1, a2., am }, де X – множина вершин, а A – множина ребер графа. Якщо ребра з множини A орієнтовані, то вони називаються дугами, а граф називають орієнтованим. Якщо ребра не мають орієнтації, то граф називають неорієнтованим. Інакше граф є змішаним. На рис.4.1 – 4.6 приведені неорієнтований і орієнтований графи відповідно.
Якщо зіставити кожному ребру число з множини С, тоді граф називають зваженим. Граф можна задати матрицями суміжності і інцидентності. Елементи матриці суміжності S графа задаються так:
Елементи матриці інцидентності
Для графа, приведеного на рис.4.3, матриця суміжності приведена на рис.4.4, а матриця інцидентності – на рис.4.5.
Якщо граф містить петлі, тобто дуги вигляду (хi, xi) тоді елементи матриці інцидентності, відповідні дугам, створюючим петлі, одночасно рівні 1 і –1, що приводить до неоднозначності матриці інцидентності. Нехай G – неорієнтований граф. Маршрутом в графі G називається така послідовність (кінцева або нескінченна) ребер a 1, a 2,... an..., що кожні два сусідні ребра ai та ai+ 1мають загальну інцидентну вершину. Одне і те ж ребро може зустрічатися в маршруті кілька разів. У кінцевому маршруті (a 1, a 2,... an) є перше ребро a 1і останнє ребро an. Вершина x 1, інцидентна ребру a 1, але не інцидентна ребру a 2, називається початком маршруту, а вершина xn, інцидентна ребру an, але не інцидентна ребру an- 1, називається кінцем маршруту. Довжиною маршруту називається число ребер, що входять в маршрут, причому кожне ребро рахується стільки раз, скільки воно входить в даний маршрут. Замкнутий маршрут називається циклом. Маршрут (цикл), в якому всі ребра різні, називається простим ланцюгом (циклом). Маршрут (цикл), в якому всі вершини (окрім першої і останньої) різні, називається елементарним ланцюгом (циклом). На рис.4.6 зображено два маршрути з вершини x1 до вершини x4: M 1= (a 1, a 2, a 4) та M 2= (a 1, a 2, a 5, a 6). Довжина маршруту M1 дорівнює 3, а довжина маршруту M2 дорівнює 4.
Поняття шляху і контура в орієнтованому графі аналогічні поняттям маршруту і циклу в неорієнтованому графі. Шляхом в орієнтованому графі називається послідовність дуг, в якій кінцева вершина всякої дуги, відмінної від останньої, є початковою вершиною наступної дуги. Число дуг шляху називається довжиною шляху. Шлях називається контуром, якщо його початкова вершина співпадає з кінцевою вершиною. Шлях (контур), в якому всі дуги різні, називається простим. Шлях (контур), в якому всі вершини, окрім першої і останньої, різні, називається елементарним. Поняттям ребра, маршруту, ланцюга, циклу в неорієнтованому графі відповідають поняття дуги, шляху, орієнтованого ланцюга, контура в орієнтованому графі.
Граф називається зв’язним, якщо кожна пара різних вершин може бути сполучена, принаймні, одним ланцюгом. Орієнтований граф називається навантаженим, якщо дугам цього графа поставлені у відповідність ваги, так що дузі (xi ,xj)зіставлено деяке число c (xi, xj)= cij, зване довжиною (або вагою, або вартістю дуги). Довжиною (або вагою або вартістю) шляху s, що складається з деякої послідовності дуг (xi, xj), називається число l (s), що дорівнює сумі довжин дуг, що входять в цей шлях, тобто l (s)=
причому підсумовування ведеться по всіх дугах(xi, xj) Матриця C = (cij) називається матрицею довжин дуг або матрицею вагів. Підграфом неорієнтованого графа G називається граф, всі вершини і ребра якого містяться серед вершин і ребер графа G. Підграф називається власним, якщо він відмінний від самого графа. Аналогічно визначається підграф орієнтованого графа. Компонентою зв’язності неорієнтованого графа називається його зв’язний підграф, що не є власним підграфом ніякого іншого зв’язного підграфа даного графа. Неорієнтованим деревом (або просто деревом) називається зв’язний граф без циклів. Остовним деревом (деревом-остовом, покриваючим деревом, скелетним деревом) зв’язного графа G називається будь-який його підграф, що містить всі вершини графа G і що є деревом.
4.2 Алгоритм побудови мінімального покриваючого дерева Нехай G – зв’язний навантажений граф. Завдання побудови мінімального остовного дерева полягає в тому, щоб з множини остовних дерев знайти таке, у якого сума довжин ребер мінімальна. Приведемо типові випадки, коли виникає необхідність побудови мінімального остовного дерева графа: а) Необхідно з’єднати n міст залізничними лініями (або автомобільними дорогами, лініями електропередач, мережею трубопроводів і так далі) так, щоб сумарна довжина ліній або вартість була б мінімальною. б) Потрібно побудувати схему електричної (комп’ютерної) мережі, в якої клеми (вузли мережі) повинні бути сполучені за допомогою проводів найменшої загальної довжини. Задачу побудови мінімального дерева-остову можна вирішити за допомогою алгоритму Краскала. Приведемо опис алгоритму по кроках. Крок 1. Відсортуємо ребра графа по неубуванню вагів. Крок 2. Вважаємо, що кожна вершина відноситься до своєї компоненти зв’язності. Крок 3. Проходимо ребра в «відсортованому» порядку. Для кожного ребра виконуємо наступну перевірку: а) якщо вершини, що сполучаються даним ребром, лежать в різних компонентах зв’язності, то об’єднуємо ці компоненти в одну, а дане ребро додаємо до мінімального дерева-остову; б) якщо вершини, що сполучаються даним ребром, лежать в одній компоненті зв’язності, то виключаємо ребро з розгляду, оскільки при включенні даного ребра утворюється цикл. Крок 4. Якщо є ще нерозглянуті ребра і не всі компоненти зв’язності об’єднані в одну, то переходимо до кроку 3, інакше алгоритм завершує роботу: а) якщо при цьому проглянуті всі ребра, але не всі компоненти зв’язності об’єднані в одну, то для початкового графа неможливо побудувати покриваюче дерево; б) якщо проглянуті всі ребра, і всі компоненти зв’язності об’єднані в одну, то для початкового графа побудовано мінімальне покриваюче дерево. Приклад 4.1. Граф G містить 5 вершин. Відстані між вершинами задані таблицею 4.1. Знайти його мінімальне дерево-остов (мінімальне покриваюче дерево).
Таблиця 4.1 – Відстані між вершинами Рішення. Оскільки матриця симетрична, можна розглядати, наприклад, тільки елементи, розташовані вище або нижче за головну діагональ:
1. Включаємо в дерево-остов ребро (1, 4). Множина вершин, включених в дерево-остов V ={1, 4} (рис.4.7). 2. Наступним кандидатом на включення в дерево-остов є ребро (2, 4). Додавання вершини 2 до множини V і ребра (2, 4) до дерева не створює циклу, оскільки вершина 2 не входить в множину V. Після додавання ребра (2, 4) до дерева множина вершин, включених в дерево-остов V ={1, 2, 4} (рис.4.8). 3. Додавання ребра (1, 2) приведе до утворення циклу (рис.4.9). Тому не включаємо це ребро в дерево-остов. 4. Наступним кандидатом на включення в дерево-остов є ребро (2, 5). Його включення не створює циклу, тому V ={1, 2, 4, 5} (рис.4.10). 5. Додавання ребра (1, 5) приведе до утворення циклу (рис.4.11). Тому не включаємо це ребро в дерево-остов. 6. Наступним кандидатом на включення в дерево-остов є ребро (4, 5). Проте його додавання приведе до утворення циклу. Тому не включаємо це ребро в дерево-остов. 7. Включення ребра (1, 3) не створює циклу, тому V ={1, 2, 3, 4, 5} (рис.4.12). 8. Оскільки всі вершини графа увійшли до дерева, то отримано покриваюче дерево з мінімальною вагою, рівною 17.
4.3 Алгоритми визначення найкоротшого шляху (Дейкстри та Флойда) між вузлами мережі Пошук шляхів із заданою кількістю дуг Нехай G = (Х, А) – зв'язний граф. Для визначення кількості шляхів, що складаються з k дуг, необхідно звести в k-у ступінь матрицю суміжності. Тоді її елемент Приклад 4.2. Для графа, приведеного на рис.4.13 зліва, знайти всі шляхи довжини 3 (тобто, знайти всі шляхи, що містять рівно три дуги). Рішення. Матриця суміжності для даного графа має вигляд, представлений на рис.4.13 справа.
Значення Щоб виявити ці шляхи, слід позначити дуги, наприклад, так, як на рис.4.14. Замість матриці суміжності введемо в розгляд матрицю, елементами якої є дуги вигляду
Виконуємо символьне множення матриць:
У таблиці 4.2 приведена матриця
Таблиця 4.2 – Представлення матриці
Відмітимо, що число доданків в кожному елементі отриманої матриці рівне числу елементів матриці
1- Алгоритм Дейкстри для пошуку найкоротшого шляху між заданою парою вершин Нехай G = (Х, А) – зв’язний граф, кожній дузі якого приписано деяке число а(x, y)³ 0. Завдання побудови найкоротшого шляху між заданою парою вершин sÎХ і tÎХ полягає в тому, щоб з множини шляхів, що сполучають вказані вершини, знайти такий, сумарна довжина дуг якого мінімальна. Для вирішення завдання можна скористатися алгоритмом Дейкстри. Приведемо його опис по кроках. Крок 1. Перед початком виконання алгоритму всі вершини не помічені. Кожній вершині хÎХ в ході виконання алгоритму привласнюється число d(x), рівне довжині найкоротшого шляху з s в х, що включає тільки помічені вершини. Покласти d(s)=0, d(x)=∞ для всіх х, відмінних від s. Помітити вершину s і покласти y = s (y – остання із помічених вершин). Крок 2. Для кожної непоміченої вершини х таким чином перерахувати величину d(x): d(x)= min {d(x), d(x)+a(y, x)}.
Якщо d(x)=∞ для всіх непомічених вершин х, закінчити процедуру алгоритму: у заданому графі відсутні шляхи між вказаною парою вершин. Інакше помітити ту з вершин x, для якої величина d(x) є найменшою. Покласти y = x. Крок 3. Якщо y = t, закінчити процедуру: найкоротший шлях з вершини s в вершину t знайдено. Інакше перейти до кроку 2. Приклад 4.3. В заданому графі G (рис.4.16) знайти найкоротший шлях між вершинами 1 і 10.
Рисунок 4.16 – Заданий граф Рішення. Перед початком виконання алгоритму вважаємо d(1)=0, d(x)=∞ для всіх х¹1; вершина 1 – остання із помічених вершин. d(2)= min {d(2), d(1)+с(1, 2)}= min {∞, 0+5}=5; d(5)= min{d(5), d(1)+с(1, 5)}= min {∞, 0+6}=6; d(x)= ∞ для всіх х¹1, 2, 5. Оскільки мінімум випав на вершину 2, то y=2 – остання із помічених вершин (рис.4.17).
d(3)=min{d(3), d(2)+с(2, 3)}=min {∞, 5+4}=9; d(5)= min{d(5), d(2)+с(2, 5)}=min {6, 5+∞}=6; d(4)= min{d(4), d(2)+с(2, 4)}=min {∞, 5+9}=14; d(x)= ∞ для всіх х¹1, 2, 3, 4, 5.
Оскільки мінімум випав на вершину 5, то y=5 – остання із помічених вершин (рис.4.18).
d(3)=min{d(3), d(5)+с(5, 3)}=min {9, 5+∞}=9; d(4)= min{d(4), d(5)+с(5, 4)}=min {14, 6+4}=10; d(7)= min{d(7), d(5)+с(5, 7)}=min {∞, 6+5}=11; d(x)= ∞ для всіх х¹1, 2, 3, 4, 5, 7.
Оскільки мінімум випав на вершину 3, то y=3 – остання із помічених вершин (рис.4.19).
d(4)=min{d(4), d(3)+с(3, 4)}=min {10, 9+3}=10; d(5)=min{d(5), d(3)+с(3, 5)}=min {6, 9+2}=6 (оцінка не зменшилася, тобто кращий шлях не знайдений); d(7)= min{d(7), d(3)+с(3, 7)}=min {11, 9+∞}=11; d(x)= ∞ для всіх х¹1, 2, 3, 4, 5, 7.
Оскільки мінімум випав на вершину 4 (з непомічених), то y=4 – остання із помічених вершин (рис.4.20).
d(6)=min{d(6), d(4)+с(4, 6)}=min {∞, 10+3}=13; d(7)= min{d(7), d(4)+с(4, 7)}=min {11, 10+∞}=11; d(x)= ∞ для всіх х¹1, 2, 3, 4, 5, 6, 7.
Оскільки мінімум випав на вершину 7, то y=7 – остання із помічених вершин (рис.4.21).
d(6)=min{d(6), d(7)+с(7, 6)}=min {13,11+∞}=13; d(8)=min{d(8), d(7)+с(7, 8)}=min(∞,11+2}=13; d(10)=min{d(10), d(7)+с(7, 10)}=min {∞,11+8}=19; d(x)= ∞ для х=9.
Оскільки мінімум випав на вершину 6, то y=6 – остання із помічених вершин (рис.4.22).
d(7)= min{d(7), d(6)+с(6, 7)}=min {11,13+5}=11 (оцінка не зменшилася, тобто кращий шлях не знайдений); d(8)=min{d(8), d(6)+с(6, 8)}=min {13,13+∞}=13; d(9)=min{d(9), d(6)+с(6, 9)}=min {∞,13+7}=20; d(10)=min{d(10), d(6)+с(6,10)}=min {19,13+6}=19.
Оскільки мінімум випав на вершину 8 (з непомічених), то y=8 – остання із помічених вершин (рис.4.23).
d(9)=min{d(9), d(8)+с(8, 9)}=min {20,13+∞}=20; d(10)=min{d(10), d(8)+с(8,10)}=min {19,13+7}=19.
Оскільки мінімум випав на вершину 10, то y=10, і на цьому алгоритм Дейкстри закінчує роботу (рис.4.24).
Таким чином, найкоротший шлях з вершини 1 у вершину 10 проходить через проміжні вершини 5 і 7 (рис.4.25). Довжина цього шляху дорівнює 19.
Пошук всіх найкоротших шляхів (алгоритм Флойда) Перенумеруємо всі вершини початкового графа цілими числами від 1 до n. Позначимо через Позначимо через Припустимо, що нам відомі: 1)найкоротший шлях з вершини i у вершину m, в якому як проміжні допускається використання тільки перших (m-1) вершин; 2)найкоротший шлях з вершини m у вершину j, в якому як проміжні допускається використання тільки перших (m-1) вершин; 3)найкоротший шлях з вершини i у вершину j, в якому як проміжні допускається використання тільки перших (m-1) вершин. По припущенню початковий граф не може містити контурів від’ємної довжини. Отже, один з двох шляхів – шлях, що співпадає з шляхом, описаним в пункті 3, або шлях, що є об’єднанням шляхів з пунктів 1–2, – повинен бути найкоротшим шляхом з вершини i у вершину j, в якому як проміжні допускається використання тільки перших m вершин. Таким чином
Приведемо покроковий опис алгоритму Флойда: Крок 1. Пронумерувати вершини початкового графа цілими числами від 1 до n. Визначити матрицю Крок 2. Для цілого m, послідовно приймаючого значення 1, 2,..., n, визначити по величинах елементів матриці
При визначенні величини кожного елементу матриці Рядки і стовпці матриці Приклад 4.4. Для графа, приведеного на рис.4.26, знайти найкоротші шляхи між будь-якою парою вершин.
Рішення. Матриця
Таблиця 4.3 – Процес обчислень матриці
Аналогічно визначаються матриці
Таблиця 4.3 – Визначення матриць
Для вирішення реальних завдань приведений вище спосіб формування найкоротших шляхів малопридатний. Зручно ввести в розгляд матрицю маршрутів R. На m-ій ітерації вона визначається як
Для розглянутого вище прикладу маємо:
Щоб скористатися матрицею
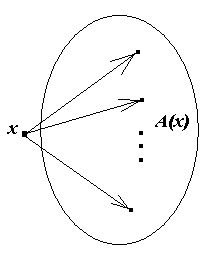
4.4 Задача про максимальний потік та мінімальний розріз в мережі Нехай G = (N, А) – зв’язний граф, в якому виділено дві вершини: s – джерело, t – стік. Кожній дузі (x, у) графа поставлено у відповідність невід’ємне число с (x, у), яке інтерпретується як максимальна кількість одиниць деякого товару, яке може бути доставлено з вершини x у вершину у за одиницю часу. Це число прийнято називати пропускною спроможністю дуги. Такий граф називають мережею, а його вершини – вузлами. Стаціонарний потік величини v з s в t в мережі G = (N, А) є функція f, що відображає множину А в множину невід’ємних чисел, що задовольняють лінійним рівнянням і нерівностям наступного вигляду:
де А(х) – підмножина множини N, що включає вершини у, що є кінцями дуг з початком у вершині х; В(х) – підмножина множини N, що включає вершини у, що є початком дуг, що входять у вершину х.
Розрізом Приведемо формулювання теореми про максимальний потік і мінімальний розріз. Теорема. Для будь-якої мережі максимальна величина потоку з s до t рівна мінімальній пропускній спроможності розрізу, відокремлюючого s і t. Завдання побудови максимального потоку між заданою парою вершин sÎN і tÎN полягає в тому, щоб з множини шляхів, що сполучають вказані вершини, знайти такі, по яких можна пропустити максимальну кількість одиниць потоку в одиницю часу. При цьому повинні дотримуватися наступні обмеження: · потік по кожній дузі не повинен перевищувати її пропускну спроможність; · потік з джерела s рівний потоку, що приходить в стік t; · для проміжних вершин кількість одиниць потоку, що потрапив в цей вузол, повинна в точності дорівнювати кількості одиниць потоку, що вийшов з цього вузла. Для вирішення завдання можна скористатися алгоритмом розстановки позначок Форда-фалкерсона. Алгоритм може починати роботу з нульового потоку. Потім обчислення розвиваються у вигляді послідовності «розстановки позначок» (операція А), кожна з яких або приводить до потоку з більшою величиною (операція В), або закінчується висновком про те, що даний потік максимальний. Всі вузли мережі знаходяться в одному з наступних станів: не помічений, помічений і не проглянутий, помічений і проглянутий. Спочатку всі вузли не помічені. Операція А (процес розстановки позначок). Джерело s отримує позначку (-, ε(s)=∞) (джерело тепер помічене і не проглянуте, решта вузлів не помічена). Вибираємо будь-який помічений і не проглянутий вузол х. Хай він має позначку
(такі вузли у тепер помічені і не проглянуті). Всім вузлам у, які після цього не помічені і для яких f(y, x) > 0 приписуємо позначку
(такі вузли у тепер помічені і не проглянуті, а вузол х після цього помічений і проглянутий). Цей загальний крок повторюваний до тих пір, поки 1)не виявиться поміченим і не проглянутим стік t; 2) або ж до тих пір, поки не можна буде помітити жоден вузол, а стік t залишиться непоміченим. У першому випадку переходимо до операції В, а в другому – алгоритм закінчив роботу, оскільки максимальний потік в мережі отриманий. Операція В (зміна потоку). Хай стік t має позначку Примітка. Пропускні спроможності дуг повинні бути цілими невід’ємними числами. Приклад 4.5. Знайти максимальний потік і мінімальний розріз, що відокремлює джерело 1 і стік 6 для мережі, приведеної на рис.4.27. Пара чисел біля кожної дуги означає пропускну спроможність і потік по дузі відповідно.
Рішення. На рис.4.28 показані позначки, отримані в ході виконання операції А на першій стадії роботи алгоритму. Джерело (вузол 1) отримало позначку (-, ∞). Потім з вузла 1 позначаються вузли 2, 3 і 4. З вузла 2 позначається вузол 5, а з вузла 3 – стік (вузол 6). Оскільки стік виявився поміченим, переходимо до операції В. Стік отримав позначку (3+, 2). Отже, f(3, 6) стане рівним 0+2=2. Переходимо до вузла 3. Оскільки він має позначку (1+, 2), то потік по дузі (1, 3) стане рівним 0+2=2.
Оскільки в результаті виконання операції В досягнуте джерело (вузол 1), то слід стерти старі позначки і знову перейти до операції А. Стан мережі приведений на рис.4.29 Жирними стрілками вказані дуги, по яких йдуть дві одиниці потоку.
Рисунок 4.29 – Стан мережі після виконання операції В
Знову виконуємо операцію А. Джерело (вузол 1) отримало позначку (-, ∞). Потім з вузла 1 позначаються вузли 2 і 4 (рис.4.30). З вузла 2 позначаються вузли 3 і 5, а з вузла 3 – стік (вузол 6). Оскільки стік виявився поміченим, переходимо до операції В. Стік отримав позначку (3+, 1). Отже, f(3, 6) стане рівним 2+1=3. Переходимо до вузла 3. Оскільки він має позначку (2+, 1), то потік по дузі (2, 3) стане рівним 0+1=1. Переходимо до вузла 1 і збільшуємо потік по дузі (1+, 3), то поті
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.013 с.) |

 Рисунок 4.1
Рисунок 4.1
 Рисунок 4.2
Рисунок 4.2
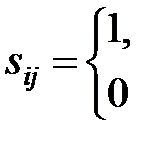
 для графа G, що складається з n вершин і m дуг, визначаються як:
для графа G, що складається з n вершин і m дуг, визначаються як:









 s.
s.
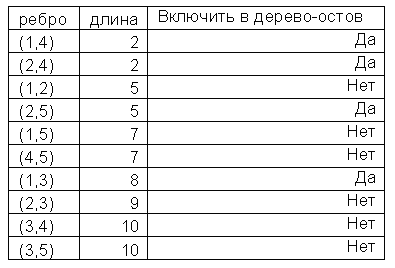
 Рисунок 4.7
Рисунок 4.7
 Рисунок 4.8
Рисунок 4.8
 Рисунок 4.9
Рисунок 4.9
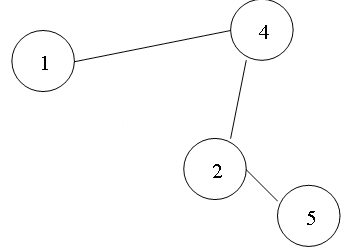 Рисунок 4.10
Рисунок 4.10
 Рисунок 4.11
Рисунок 4.11
 Рисунок 4.12
Рисунок 4.12
 дасть кількість шляхів довжини k із вершини
дасть кількість шляхів довжини k із вершини  до вершини
до вершини  .
.

 та
та  виглядають так:
виглядають так:
 ,
, 
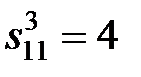 означає, що з вершини 1 у вершину 1 існує 4 шляхи довжини 3,
означає, що з вершини 1 у вершину 1 існує 4 шляхи довжини 3,  — з вершини 1 у вершину 2 – 5 шляхів довжини 3 і так далі
— з вершини 1 у вершину 2 – 5 шляхів довжини 3 і так далі , r = 1, 2, …., 10 (рис.4.15).
, r = 1, 2, …., 10 (рис.4.15).





 по стовпцях.
по стовпцях.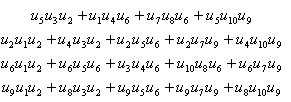


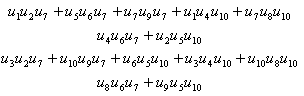


 -3-
-3-  -2-
-2-  -1, 1-
-1, 1-  -2-
-2-  -3-
-3-  -1, 1-
-1, 1-  -4-
-4-  -3-
-3-  -1, 1-
-1, 1-  -3-
-3-  -4-
-4-  -1.
-1.









 довжину найкоротшого шляху з вершини i до вершини j, який як проміжні може містити тільки перші m вершин графа. Якщо ж між вершинами i та j не існує жодного шляху вказаного типу, то умовно вважатимемо, що
довжину найкоротшого шляху з вершини i до вершини j, який як проміжні може містити тільки перші m вершин графа. Якщо ж між вершинами i та j не існує жодного шляху вказаного типу, то умовно вважатимемо, що  З даного визначення величини
З даного визначення величини  витікає, що величина
витікає, що величина  є довжиною найкоротшого шляху з вершини i до вершини j, що не має проміжних вершин, тобто, довжиною найкоротшої дуги, що сполучає вершини i та j (якщо такі дуги присутні в графі). Вважатимемо, що
є довжиною найкоротшого шляху з вершини i до вершини j, що не має проміжних вершин, тобто, довжиною найкоротшої дуги, що сполучає вершини i та j (якщо такі дуги присутні в графі). Вважатимемо, що 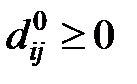 для всіх i та j (1 £ i ¹ j £ n). Для будь-якої вершини i покладемо
для всіх i та j (1 £ i ¹ j £ n). Для будь-якої вершини i покладемо 
 матрицю розмірності n ´ n, елемент якої, розташований на перетині i -го рядка та j -го стовпця, співпадає з
матрицю розмірності n ´ n, елемент якої, розташований на перетині i -го рядка та j -го стовпця, співпадає з  . Якщо в початковому графові відома довжина кожної дуги, то можна сформувати матрицю
. Якщо в початковому графові відома довжина кожної дуги, то можна сформувати матрицю 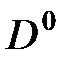 . Наша мета полягає у визначенні матриці
. Наша мета полягає у визначенні матриці  , що представляє найкоротші шляхи між всіма вершинами початкового графа. У алгоритмі Флойда як початкова виступає матриця
, що представляє найкоротші шляхи між всіма вершинами початкового графа. У алгоритмі Флойда як початкова виступає матриця  . Потім по ній обчислюється матриця
. Потім по ній обчислюється матриця  , а по ній – матриця
, а по ній – матриця  і так далі. Процес повторюється до тих пір, поки не буде обчислена матриця
і так далі. Процес повторюється до тих пір, поки не буде обчислена матриця  .
.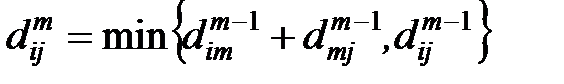 .
. , задавши величину кожного її елементу
, задавши величину кожного її елементу  рівній довжині найкоротшої дуги, що сполучає вершини i і j. Якщо в початковому графі вказані вершини не з’єднуються дугами, покласти
рівній довжині найкоротшої дуги, що сполучає вершини i і j. Якщо в початковому графі вказані вершини не з’єднуються дугами, покласти 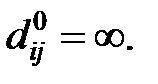 Крім того, покласти
Крім того, покласти  для всіх i (1 £ i£ n).
для всіх i (1 £ i£ n). величини елементів матриці
величини елементів матриці  , використовуючи співвідношення
, використовуючи співвідношення .
. фіксувати відповідний найкоротший шлях. Після закінчення даної процедури величина елементу
фіксувати відповідний найкоротший шлях. Після закінчення даної процедури величина елементу  матриці
матриці  визначає величину найкоротшого шляху, що веде з вершини i у вершину j.
визначає величину найкоротшого шляху, що веде з вершини i у вершину j. для яких i = m і j = m, називатимемо базовими. Неважко відмітити, що в таких рядках і стовпцях значення матриці можна не перераховувати, оскільки вони повністю співпадають з відповідними значеннями матриці
для яких i = m і j = m, називатимемо базовими. Неважко відмітити, що в таких рядках і стовпцях значення матриці можна не перераховувати, оскільки вони повністю співпадають з відповідними значеннями матриці  .
.

 для даного графа приведена на рис.4.26 зліва. Весь процес обчислень приведений в таблиці 4.3.
для даного графа приведена на рис.4.26 зліва. Весь процес обчислень приведений в таблиці 4.3.


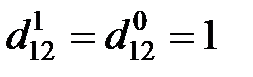






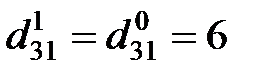







 Отримані результати приводяться в таблиці 4.4.
Отримані результати приводяться в таблиці 4.4.





 де
де  — перший проміжний вузол найкоротшого шляху з i до j, вибраний серед множини { 1, 2., m } (i ¹ j ¹ m). Алгоритм починає роботу при
— перший проміжний вузол найкоротшого шляху з i до j, вибраний серед множини { 1, 2., m } (i ¹ j ¹ m). Алгоритм починає роботу при 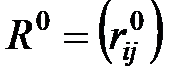 , де
, де  . На m-ій ітерації елемент
. На m-ій ітерації елемент  може бути отриманий з наступного співвідношення:
може бути отриманий з наступного співвідношення:










 для визначення шляху, наприклад, з вершини 3 у вершину 2, проглядаємо елемент
для визначення шляху, наприклад, з вершини 3 у вершину 2, проглядаємо елемент 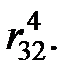 Оскільки він рівний 4, це означає, що вершина з номером 4 є першою проміжною в цьому шляху. Далі проглядаємо елемент
Оскільки він рівний 4, це означає, що вершина з номером 4 є першою проміжною в цьому шляху. Далі проглядаємо елемент  Оскільки він рівний 1, це означає, що вершина з номером 1 є другою проміжною в цьому шляху. Далі проглядаємо елемент
Оскільки він рівний 1, це означає, що вершина з номером 1 є другою проміжною в цьому шляху. Далі проглядаємо елемент  Оскільки елемент рівний номеру кінцевої вершини 2, отримуємо, що шуканий шлях проходить по дугах (3, 4), (4, 1) і (1, 2) (що відповідає результату з таблиці 4.3).
Оскільки елемент рівний номеру кінцевої вершини 2, отримуємо, що шуканий шлях проходить по дугах (3, 4), (4, 1) і (1, 2) (що відповідає результату з таблиці 4.3).

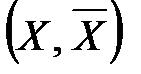 у мережі G = (N, А), що відокремлює вузли s і t, називається множина дуг, де
у мережі G = (N, А), що відокремлює вузли s і t, називається множина дуг, де  . При цьому
. При цьому 
 . Всім вузлам у, які не помічені і для яких f(x, y) < c(x, y) приписуємо позначку
. Всім вузлам у, які не помічені і для яких f(x, y) < c(x, y) приписуємо позначку  , де
, де
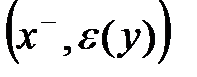 , де
, де
 . Якщо він має позначку
. Якщо він має позначку  , то f(y, t) замінюємо на f(y, t)+ε(t); якщо він має позначку
, то f(y, t) замінюємо на f(y, t)+ε(t); якщо він має позначку  , то f(y, t) замінюємо на f(y, t)-ε(t). У будь-якому з цих випадків переходимо до вузла у. Взагалі, якщо вузол у має позначку
, то f(y, t) замінюємо на f(y, t)-ε(t). У будь-якому з цих випадків переходимо до вузла у. Взагалі, якщо вузол у має позначку 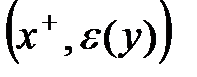 , то f(x, y) замінюємо на f(x, y)+ε(t), а якщо він має позначку
, то f(x, y) замінюємо на f(x, y)+ε(t), а якщо він має позначку  , то f(x, y) замінюємо на f(x, y)-ε(t) і переходимо до вузла х. Коли ми досягнемо джерела s, зміна потоку припиняється. Потрібно стерти всі старі позначки і знов перейти до операції А.
, то f(x, y) замінюємо на f(x, y)-ε(t) і переходимо до вузла х. Коли ми досягнемо джерела s, зміна потоку припиняється. Потрібно стерти всі старі позначки і знов перейти до операції А.





