Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛЕКЦІЯ 8 «Позиційні ігри та ігри декількох осіб» ⇐ ПредыдущаяСтр 7 из 7
Анотація Поняття про позиційні ігри. Кооперативні ігри та методи їх дослідження.Некооперативна гра двох осіб. Кооперативна гра двох осіб. Переговорна множина. Схема алгоритму переговорної множини.
8.1 Поняття про позиійні ігри Позиційна гра – це природне розширення матричної гри двох гравців з нульовою сумою, в якій може брати участь скінченна кількість гравців, кожен з яких може робити послідовно скінченну кількість ходів, причому деякі з них можуть бути випадковими, а інформація про них може змінюватися від одного до іншого ходу. Такі ігри можуть бути формалізовані, певним чином перетворені до гри, що еквівалентна деякій матричній грі двох осіб з нульовою сумою. Процес приведення позиційної гри до матричної називається нормалізацією, а отримана матрична гра – грою в нормальній формі. Розглянемо наступний приклад. Дві корпорації мають бажання встановити між собою ділові зв’язки і вирішити питання про побудову на території другої корпорації виробництва. Гра складається з трьох ходів. Перша корпорація обирає число з множини {1, 2}. Після цього друга корпорація обирає з множини двох можливих {1, 2}, знаючи, який вибір здійснила перша корпорація на першому ході. Третій хід робить перша корпорація: знаючи, який хід зробила друга корпорація, та пам’ятаючи про свій вибір на першому кроці, обирає число з множини {1, 2}. На цьому гра завершується і розподіляються виграші: перший гравець виплачує другому певну суму, визначену функцією М(x,y, z) яка визначена наступним чином в залежності від вибору гравцями 1-го – 3-го ходів x,yтаz відповідно: М(1, 1, 1) = -2; М(1, 1, 2) = -1; М(1, 2, 1) = 3; М(1, 2, 2) = -4; М(2, 1, 1) = 5; М(2, 1, 2) = 2; М(2, 2, 1) = 2; М(2, 2, 2) = 6. Змістова інтерпретація цієї гри є наступною: Хід 1. 1-а корпорація здійснює вибір з двох альтернатив: х =1 – запропонувати 2-й побудувати на її теорії складальне виробництво комп’ютерів, х = 2 – побудувати виробництво мікропроцесорів. Хід 2. 2-а корпорація, знаючи, яку альтернативу обрала 1-а на першому ході, здійснює вибір з двох альтернатив: y = 1 – будувати складальне виробництво та запропонувати це 1-й корпорації; y = 2 – будувати виробництво мікропроцесорів та запропонувати це 1-й. Хід 3. 1-а корпорація, знаючи вибір 2-ї на другому ході та пам’ятаючи свій вибір на першому ході, здійснює вибір з двох альтернатив: z = 1 – погодитися з пропозицією 2-ї, z = 2 – не погодитися з пропозицією 2-ї.
Після того, як зроблені ходи, партія зіграна, і 1-а корпорація отримує суму М(x,y, z). Для нормалізації цієї гри необхідно відтворити стратегіях 1-го та 2-го гравця. Стратегії 2-го гравця: В1 – обрати y = 1 не зважаючи на вибір 1-го гравця на першому ході; В2 – обрати y = 2 не зважаючи на вибір 1-го гравця на першому ході; В3 – погодитися з вибором 1-го гравця на першому ході, тобто обрати y = 1, якщо х =1, і y = 2, якщо х = 2; В4 – не погодитися з вибором 1-го гравця на першому ході, тобто обрати y = 2, якщо х =1, і y = 1, якщо х = 2. Таким чином 2-й гравець має 4 стратегії. Стратегії першого гравця будуються аналогічно з врахуванням раніше зроблених виборів; вибір на першому кроці дає дві можливості, після вибору другого гравця з’являється чотири варіанти, і реалізація на третьому ході – 8 стратегій дії для 1-го гравця Таким чином, стратегію першого гравця зображатимемо за допомогою трійки (і, і1, і2) – де і – вибір 1-го гравця на 1-му ході; і1 –вибір 1-го гравця на 3-му ході за умови вибору на 2-му ході 2-м гравцем y = 1; і2 –вибір 1-го гравця на 3-му ході за умови вибору на 2-му ході 2-м гравцем y = 2. Враховуючи відтворені стратегії, будуємо матрицю цієї гри:
Розв’язком гри є дві сідлові точки, ціна гри – 5. Побудуємо дерево позиційної гри. В цьому дереві вузол позначатиме номер гравця, що робить хід, а другі – його хід. Листя дерева відображатимуть виграші, а кожний шлях від кореня до листка – партію. Для відображення необхідних даних про зроблені вибори при певних ходах гравців за умов їх різної інформованості на різних ходах на дереві позиційної гри пунктиром позначатимемо інформаційні множини вузлів.
Оскільки 1-й хід робить 1-й гравець, то корінь відповідатиме ходу 1-го гравця та позначається 1. 2-й гравець робить 2-й хід, а тому вузли наступного рівня позначені 2, і так як йому відомий вибір 1-го гравця на першому ході, то він, здійснюючи свій хід, в момент здійснення ходу знає точно, де він (на якій гілці дерева) знаходиться – а тому кожен вузол нижнього рівня утворює окрему інформаційну множину (внаслідок повного знання ходів кожен з вузлів дерева цієї гри є окремою інформаційною множиною).
Рисунок8.1 – Інформаційні множини вузлів при знанні всіх ходів Приклад 2. Порівняно з попереднім прикладом третій хід робить 1-й гравець, але вже не пам’ятаючи про те, який хід він зробив першим та не знаючи, який другий хід зробив другий гравець (1-го гравця можна уявити, як 2 особи, що знаходяться в окремих кімнатах та які не мають змоги обмінюватися інформацією). Відповідне дерево гри з інформаційними множинами наведене на рис.8.2.
Рисунок8.2 – Інформаційні множини при частковому знанні
Проведемо гру до нормальної форми. У 2-го гравця є 4 таких же стратегії, як і в попередньому випадку. У 1-го гравця можливості зменшуються за рахунок браку інформації: оскільки він на 3-му ході не знає попередніх виборів, то його стратегія складається з пари чисел (x, z), тобто обрати 1 або 2 на 1-му ході та 1 або 2 на 3-му ході. Відповідна матриця гри буде мати наступний вигляд:
Отримана гра не має сідловок точки. Розв’язуючи гру в мішаних стратегіях, отримаємо мішані стратегії 1-го гравця – (0, 0, 4/7, 3/7), 2-го гравця – (4/7, 3/7, 0, 0), та ціна гри становитиме v = 26/7. Таким чином, в загальному випадку втрата інформації зменшує ціну гри.
8.2 Кооперативні ігри та методи їх дослідження Конфлікті ситуації не завжди мають антагоністичнийхарактер. Дуже часто учасники конфлікту, переслідуючи свої цілі, готові вступити в переговори один з одним, укладаючи деякі угоди чи навіть об’єднати свої зусилля в надії отримати з цього переваги. Одним з найважливіших висновків теорії ігор – це те, що певні форми кооперування гравців за умови зовнішньо різних їх прагнень дійсно мають сенс. Це частково пояснюється великою цінністю інформації., яка може бути передана від одного до іншого учасника гри, зростаючим значенням рішень, що приймаються спільно, синергічним ефектом від хоча б часткового об’єднання ресурсів. Ігри двох осіб посідають центральне місце у всій теорії ігор. Серед таких ігор виділяються біматричні ігри. Причини цього наступні. Біматричні ігри адекватніше відображають реальні конфлікти двох осіб порівняно з матричними, що використовуються для описання конфліктів з повною суперечністю і несумісністю інтересів, з відсутністю можливості компромісів; в таких конфліктах зростання прибутку одного гравця завжди означає збільшення втрат іншого. В житті такі конфлікти зустрічаються порівняно не частою Можна було б піддатися спокусі розглядати війну як крайній приклад зіткнення інтересів, але, взагалі кажучи, війна не є строгим суперництвом, оскільки обидві сторони вважають нічию кращим результатом, аніж взаємне знищення. Хоча локальне зіткнення або повітряний бій, очевидно, доцільно розглядати як гру зі строгим суперництвом. Але взагалі для описання військових конфліктів оперативно-тактичного плану, для яких приманна наявність не менш ніж двох ієрархічно пов’язаних ланок «напад – оборона», звичайно як адекватні використовуються біматричні ігри.
Біматричні ігри – це скінченні ігри двох осіб з довільною сумою, тобто такі, для яких не обов’язково виконується умова aij = -bij (тобто виграш одного з гравців – це програш іншого. Ці ігри описуються або за допомогою двох матриць А та В – виграшів кожного гравця, або ж за допомогою складної матриці, елементами якої є пари (aij, bij).
Біматрична гра – це найпростіша ігрова модель, що припускає можливість співробітництва. Гра з нестрогим суперництвом, є грою, в якій не має однозначного суперника, тому що існує принаймні одна пара ситуацій х та х*, така, що один гравець віддає перевагу ситуації х* перед ситуацією х. Для таких ігор неможливо обрати функції корисності гравців так, щоб сума їх дорівнювала нулю; тому терміни «ігри з нестрогим суперництвом» та «ігри з ненульовою сумою» є еквівалентними. Більшість економічних, політичних і військових конфліктів інтересів можна представити у формі ігор лише в тому випадку, якщо визнати властиве їх нестроге суперництво. В іграх зі строгим суперництвом гравці не можуть досягати обопільної вигоди посередництвом якого-небудь співробітництва; в іграх з нестрогим суперництвом, навпаки, такий обопільний виграш завжди можливий. Існують дві різновидності бінарних ігор – безкоаліційні, що забороняють будь-яку співробітництво, та кооперативні, що дозволяють співробітництво. Результат біматричної безкоаліційної гри рідко можна передбачити, оскільки зв’язки між виграшами сторін відсутні, і з’являється можливість діяти самостійніше. Значення середніх виграшів гравців А та В в біматричній грі рівні відповідно:
Ситуація рівноваги для бінарної гри – це така пара (x, y) для якої виконується співвідношення
та природні обмеження:
Такі ситуації рівноваги в бінарній грі існують завжди – відповідна теорема про існування ситуації рівноваги в мішаних стратегіях для скінчених неантагоністичних ігор двох осіб доведена Нешем (NashJ.F.). Однак ця теорема не дає інформації про те, яким чином знайти ці ситуації рівноваги. Різноманітні алгоритми для знаходження всіх ситуацій рівноваги запропоновані багатьма авторами. Таким чином, виграші гравців у біматричних іграх задаються звичайними матричними добутками:
Розглянемо тепер основні ідеї ігор двох осіб з ненульовою сумою. 8.3Некооперативна гра двох осіб Нехай задана гра двох осіб з матрицею (8.1). В теорії розглядаються в основному дві стратегії поведінки гравців – це максимінна стратегія і так звана стратегія загрози. Максимінна стратегія – це стратегія украй обережної людини, яка, розраховуючи на якнайгіршу ситуацію, хотіла би мати в цьому випадку максимум можливого. Якщо один з гравців застосовує свою оптимальну стратегію х* = (х1*, …, хm*), то інший не може покращити своє становище, тобто для оптимальної стратегії справедливі співвідношення
Перетворимо цю задачу здійснивши підстановку
Здійснивши підстановку
Друга можлива стратегія – це стратегія загрози, за якої гравець ставить за мету не виграти самому, а дати можливість виграти другому гравцеві якнайменше (при цьому в бінарній грі він і сам може виграти найменше!). Станемо знову на позицію першого гравця. Хай він знову застосовує мішану мінімаксну стратегію (прагне мінімізувати виграш 2-го гравця) х* = (х1*, …, хm*). Таким чином, застосовуючи її, він рахує не свій виграш, а виграш другого гравця. Якщо другий гравець робить хід j то його середній виграш становитиме
Перетворимо цю задачу, здійснивши підстановку
Здійснивши підстановку
Розглянемо докладніше випадок n = m = 2. Тоді матриця виплат гри має вигляд: B1 B2
y1 y2 Відобразимо геометричну максимінну стратегію і стратегію загрози першого гравця. Почнемо з максимінної стратегії. Нехай перший гравець обирає стратегію А1 з ймовірністю х1, х2 = 1-х1. За умови вибору гравцем В стратегії В1 середній виграш першого гравця становитиме a11x1 + a21(1 - x1).
За умови вибору гравцем В стратегії В2 середній виграш першого гравця становитиме a12x1 + a21(1 - x1) = a12x1 + a22(1 - x1) = v, отримаємо оптимальне значення середнього виграшу гравця А у випадку застосування ним своєї максимінної стратегії. Аналогічні рівняння можна виписати також і для випадку стратегії загрози.
Рисунок 8.3 – Геометрична ілюстрація максимінної стратегії та стратегії загрози
У випадку максимінної стратегії гравець А гарантує собі виграш, не менший за v (рис. 8.3а), але при цьому згоджується з тим, що припускає і більший виграш гравця В порівняно з застосуванням стратегії загрози (значення w ' на рис. 8.3б). І навпаки, діючи з позиції стратегії загрози, гравець А гарантує для гравця В отримання мінімального виграшу, але разом з тим і зменшує свій середній виграш порівняно з максимінною стратегією (відомий підхід з точки зору «нехай мені буде гірше, але щоб у сусіда було найгірше»). 8.4Кооперативна гра двох осіб. Переговорна множина Розглянемо гру з наступною матрицею виплат: y1-y
Нехай гравець А використовує мішану стратегію (х; 1–х), В – стратегію (y; 1-y). Тоді середні виграші гравців становитимуть:
Таким чином, ми побудували відображення x, y в v, w. 0≤x≤ 1, 0 ≤y ≤ 1. Відображаючи всі можливі варіанти x, y в простір v, w, отримаємо наступну фігуру (рис. 8.4), обмежену прямими, що проходять через пари точок (-1; -1), (1, 2) і (-1, -1), (2, 1), а також шматком параболи 5(v-w)2 = 2(v+w)-1. В ній є «провал», обмежений саме цією параболою.
Рисунок 8.4 – Відображення прикладу кооперативної гри за умови повного суперництва
Повернемося до загального випадку гри двох осіб з матрицею виплат (8.1) і припустимо, що гравці мають нагоду домовлятися про сумісні дії. В чому полягають ці сумісні дії? Раніше стратегія Аі першого гравця обиралася з вірогідністю хі, стратегія Bj з вірогідністю yj, і стратегії обох гравців були незалежні, так що комбінація (Аі, Вj) з’являлася з вірогідністю. хіyj. Зараз ходи обираються спільно і тому комбінація стратегій (Аі, Вj) з’являється з деякою сумісною вірогідністю рij Сумісна гра зводиться таким чином, до вибору сумісної мішаної стратегії рij При цьому очевидно:
При такій сумісній мішаній стратегії середні виграші першого і другого гравців рівні відповідно:
Представимо собі множину (v, w). Яку область заповнять значення, що отримані з наведених формул? Виявляється,що ця область є опуклою оболонкою образів точок з координатами (aij, bij). Так для наведеного вище прикладу гри область R є опукла оболонка точок (-1, -1), (2, 1) і (1, 2) (див. рис. 8.5)
Рисунок 8.5 – відображення прикладу кооперативної гри за умови співробітництва
Порівнявши цю область з тією, яка зображена на рис. 8.4. бачимо, що застосування сумісних стратегій дозволило заповнити ту «западину», яка була при некооперативній грі. Про що ж тепер можуть домовитися гравці? Нехай v* і w* -максимінні виграші першого і другого гравців відповідно (рис. 8.6). Нанесемо на нашу множину R точку з координатами точкою (v*,w*). Ця точка називається точкою statusquo. Очевидно, що жоден з гравців не погодиться одержувати в результаті сумісної гри менше ніж дає йому максимінна стратегія – навіщо йому така домовленість, якщо він може гарантувати собі без жодних домовленостей v* або w*.
Рисунок 8.6 – Множина Парето-опримальних розв’язків гри
Тому з нашої множини розв’язків відразу зникає область, де v<v* та w<w*. Розглянемо область, що тепер залишилася і визначається сумісною дією обмежень (v ≥ v*) ∧ (w ≥ w*). Задачу можна розглядати як двокритерійну з критеріями (v*,w*). Як нескладно визначити, множину Парето-оптимальних (недомінованих) розв’язків утворюють всі точки, що знаходяться на ламаній А – В – С. Очевидно, що якщо точка (v,w) домінується точкою (v',w'), то в процесі торгівлі гравці безболісно відмовляться від точки (v,w) на користь точки (v',w'),оскільки при такому переході хоча б одному стає краще, а іншому – не гірше. Очевидно, що точки, які домінують точку (v,w), знаходяться правіше і вище на множині R. Тому множина Парето-оптимальних розв’язків називається також переговорною множиною для гравців А та В. Переговорна множина на рис. 8.5 – це відрізок прямої, що сполучає точки (1, 2) і (2, 1). До чого гравці домовляться – наперед сказати не можна, оскільки на цій множині інтереси гравців прямо протилежні. Результат залежить від уміння вести переговори і лежить за межами математичного дослідження. Отже, в певному значенні, вирішити біматричну кооперативну гру двох осіб означає побудувати переговорну множину. 8.5 Схема алгоритму побудови переговорної множини Крок 1. Побудова образу всіх можливих мішаних стратегій x, y,
в просторі (v,w). Крок 2. Побудова опуклої оболонки образу припустимих стратегій і просторі (v,w). Крок 3. Знаходження максимінних виграшів кожного з гравців – точки statusquo. Крок 4. Побудова множини Парето-оптимальних розв’язків як «північно-східної границі» оптимального образу в просторі (v,w), для якої виконуються умови (v ≥ v*) ∧ (w ≥ w*). Слід відзначити, що конкретні реалізації алгоритмів для біматричної гри з числом стратегій, що більше 2, є достатньо складними.
ЛЕКЦІЯ 9 «Нечіткі множини» Анотація Еволюція теорії нечітких множин. Поняття нечітких множин. Основні характеристики нечітких множин. Функція приналежності. Операції над нечіткими числами. Операції над нечіткими множинами. Наочне представлення операцій над нечіткими множинами. Переваги та застосування нечітких систем
9.1 Еволюція теорії нечітких множин Теорія множин – розділ математики, в якому вивчаються загальні властивості множин. Теорія множин лежить в основі більшості математичних дисциплін; вона зробила глибокий вплив на розуміння предмету самої математики. До другої половини XIX століття поняття «множини» не розглядалося як математичне («множина книг на полиці», «множина людських чеснот» і т. д. – все це чисто побутові обороти мови). Положення змінилося, коли німецький математик Георг Кантор розробив свою програму стандартизації математики, в рамках якої будь-який математичний об'єкт повинен був виявлятися тою або іншою «множиною». Наприклад, натуральне число, по Канторові, слід було розглядати як множину, що складається з єдиного елементу іншої множини, званої «натуральним рядом», – який, у свою чергу, сам є множиною, що задовольняє так званим аксіомам Пеано. Напевно, самою вражаючою людського інтелекту є здатність ухвалювати правильні рішення в умовах неповної і нечіткої інформації. Побудова моделей наближених роздумів людини і використання їх в комп'ютерних системах представляє сьогодні одну з найважливіших проблем науки. Основи нечіткої логіки були закладені в кінці 60-х років в роботах відомого американського математика Лотфі Заде. Дослідження такого роду було викликано зростаючим незадоволенням експертними системами. Хвалений "штучний інтелект", який легко справлявся із завданнями управління складними технічними комплексами, був безпорадним при простих висловах повсякденному життю, типу "Якщо в машині перед тобою сидить недосвідчений водій – тримайся від неї подалі". Для створення дійсно інтелектуальних систем, здатних адекватно взаємодіяти з людиною, був необхідний новий математичний апарат, який переводить неоднозначні життєві твердження в мову чітких і формальних математичних формул. Першим серйозним кроком в цьому напрямі стала теорія нечітких множин, розроблена Заді. Його робота "Fuzzy Sets", опублікована в 1965 році в журналі "Information and Control", заклала основи моделювання інтелектуальної діяльності людини і стала початковим поштовхом до розвитку нової математичної теорії. Він же дав і назву для нової області науки - "fuzzy logic" (fuzzy – нечіткий, розмитий, м'який). На відміну від булевої алгебри, у котрій існує лише дві величини (0 та 1, правда чи неправда) у нечіткій логіці існують також перехідні величини (стани). Існує легенда про те, яким чином була створена теорія "нечітких множин". Одного разу Заде мав довгу дискусію зі своїм другом щодо того, чия з дружин привабливіша. Термін "приваблива" є невизначеним і в результаті дискусії вони не змогли прийти до задовільного підсумку. Це змусило Заде сформулювати концепцію, яка виражає нечіткі поняття типу "приваблива" в числовій формі. Подальші роботи професора Лотфі Заде і його послідовників заклали фундамент нової теорії і створили передумови для впровадження методів нечіткого управління в інженерну практику. Апарат теорії нечітких множин, продемонструвавши ряд багатообіцяючих можливостей застосування - від систем управління літальними апаратами до прогнозування підсумків виборів, виявився разом з тим складним для втілення. Враховуючи наявний рівень технології, нечітка логіка зайняла своє місце серед інших спеціальних наукових дисциплін - десь посередині між експертними системами і нейронними мережами. Тріумфальний хід нечіткої логіки по світу почався після доказу в кінці 80-х Бартоломеєм Косько знаменитої теореми FAT (Fuzzy Approximation Theorem). У бізнесі і фінансах нечітка логіка отримала визнання після того, як в 1988 році експертна система на основі нечітких правил для прогнозування фінансових індикаторів єдина передбачила біржовий крах. І кількість успішних фаззі-застосувань в даний час обчислюється тисячами. Третій період почався з кінця 80-х років і до цих пір. Цей період характеризується бумом практичного застосування теорії нечіткої логіки в різних сферах науки і техніки. До 90-го року з'явилося близько 40 патентів, що відносяться до нечіткої логіки (30 - японських). Сорок вісім японських компаній створюють лабораторію LIFE (Laboratory for International Fuzzy Engineering), японський уряд фінансує 5-річну програму по нечіткій логіці, яка включає 19 різних проектів, - від систем оцінки глобального забруднення атмосфери і передбачення землетрусів до АСОВІ заводських цехів. Результатом виконання цієї програми була поява цілого ряду нових масових мікрочіпів, що базуються на нечіткій логіці. Сьогодні їх можна знайти в пральних машинах і відеокамерах, цехах заводів і моторних відсіках автомобілів, в системах управління складськими роботами і бойовими вертольотами. У США розвиток нечіткої логіки йде по шляху створення систем для великого бізнесу і військових. Нечітка логіка застосовується при аналізі нових ринків, біржовій грі, оцінки політичних рейтингів, виборі оптимальної цінової стратегії і тому подібне. З'явилися і комерційні системи масового застосування. Зсув центру досліджень нечітких систем у бік практичних застосувань привів до постановки цілого ряду проблем, зокрема: нова архітектура комп'ютерів для нечітких обчислень; елементна база нечітких комп'ютерів і контроллерів; інструментальні засоби розробки; інженерні методи розрахунку і розробки нечітких систем управління, і тому подібне. Основні зусилля кібернетики зараз направлені на створення штучного інтелекту, що не поступається людському мозку. Оскільки комп'ютери розуміють тільки мову математики, то виникла необхідність представлення нечітких понять у вигляді математичних змінних, названих лінгвістичними. Сукупність лінгвістичних змінних (мало, багато...) складає нечітка множина. Наприклад, вік (молодий + не молодий + старий + немолодий +.). Для опису нечітких множин вводяться поняття нечіткої і лінгвістичної змінних. Нечітка змінна описується набором (N,X,A), де N – це назва змінної, X – універсальна множина (область міркувань), A – нечітка множина на X. Значеннями лінгвістичної змінної можуть бути нечіткі змінні, тобто лінгвістична змінна знаходиться на більш високому рівні, чим нечітка змінна. Кожна лінгвістична змінна складається з: ¾ назви; ¾ множини своїх значень, яка також називається базовою терм–множиною T. Елементами базової терм-множини є назви нечітких змінних; ¾ універсальної множини X; ¾ синтаксичного правила G, за яким генеруються нові терми із застосуванням слів природної або формальної мови; ¾ семантичного правила P, яке кожному значенню лінгвістичної змінної ставить у відповідність нечітку підмножину множини X. Розглянемо таке нечітке поняття як «Ціна акції». Це і є назва лінгвістичною змінною. Сформуємо для неї базову терм-множину, яка складатиметься з трьох нечітких змінних: «Низька», «Помірна», «Висока» і задамо область міркувань у вигляді X=[100; 200] (одиниць). Останнє, що залишилося зробити – побудувати функції приналежності для кожного лінгвістичного терма з базового терм-множини T. Ступінь приналежності може трактуватися по різному в залежності від завдання, в якій використовується нечітка множина. Можливі трактування ступеня приналежності: ¾ ступінь відповідності поняттю А, ¾ ймовірність, ¾ можливість, ¾ корисність, ¾ істинність, ¾ правдоподібність, ¾ значення функції та ін. Для кожної трактування ступеня приналежності розроблені свої методи побудови функцій приналежності. У ряді моделей м'яких обчислень функції приналежності задаються досить довільно в параметричному вигляді. Наприклад, функції приналежності нечітких множин можуть спочатку задаватися в моделі так, щоб вони "рівномірно покривали" область визначення X, а потім налаштовуватися в результаті зміни їх параметрів в процесі налагодження моделі.
9.2 Поняття нечітких множин Хай E - універсальна множина, x - елемент E, а R – певна властивість. Звичайна (чітка) підмножина A універсальної множини E, елементи якої задовольняють властивість R, визначається як множина впорядкованої пари A = {µA (х) /х}, де µA(х) – характеристична функція, що приймає значення 1, коли x задовольняє властивості R, і 0 – в іншому випадку. Нечітка підмножина відрізняється від звичайної тим, що для елементів x з E немає однозначної відповіді "ні" щодо властивості R. У зв'язку з цим, нечітка підмножина A універсальної множини E визначається як множина впорядкованою парі A = {µA(х) /х}, де µA(х) - характеристична функція приналежності (або просто функція приналежності), що приймає значення в деякій впорядкованій множині M (наприклад, M = [0, 1]). Функція приналежності указує ступінь (або рівень) приналежності елементу x до підмножини A. Множину M називають множиною ознак. Якщо M = {0,1}, тоді нечітка підмножина A може розглядатися як звичайна або чітка множина. Розглянемо множину X всіх чисел від 0 до 10. Визначимо підмножину A множини X всіх дійсних чисел від 5 до 8. A = [5, 8] Покажемо функцію приналежності множині A, ця функція ставить у відповідність число 1 або 0 кожному елементу в X, залежно від того, належить даний елемент підмножині A чи ні. Результат представлений на рисунку 9.1.
Рисунок9.1 – Зображення приналежності звичайної (чіткої) множини
Можна інтерпретувати елементи, відповідні 1, як елементи, що знаходяться в множині A, а елементи, відповідні 0, як елементи, що не знаходяться у множині A. Ця концепція використовується в багатьох областях. Але існують ситуації, в яких даній концепції не вистачатиме гнучкості. У даному прикладі опишемо множину молодих людей. Формально можна записати так B = { множина молодих людей} Оскільки, взагалі, вік починається з 0, то нижня межа цієї множини повинна бути нулем. Верхню межу визначити складніше. Спочатку встановимо верхню межу, скажімо, рівну 20 рокам. Таким чином, маємо B як чітко обмежений інтервал, буквально: B = [0, 20]. Виникає питання: чому хтось в свій двадцятирічний ювілей – молодий, а відразу наступного дня вже не молодий? Очевидно, це структурна проблема, і якщо пересунути верхню межу в іншу точку, то можна поставити таке ж питання. Природніший шлях створення множини B полягає в ослабленні строгого ділення на молодих і не молодих. Зробимо це, виносячи не тільки чіткі думки "Так, він належить множині молодих людей" чи ні, вона не належить множині молодих людей", але і гнучкі формулювання "Так, він належить до досить молодих людей" чи ні, він не дуже молодий". Розглянемо як за допомогою нечіткої множини визначити вираз "він ще молодий". У першому прикладі ми кодували всі елементи множини за допомогою 0 чи 1. Простим способом узагальнити дану концепцію є введення значень між 0 і 1. Реально можна навіть допустити нескінченне число значень між 0 і 1, в одиничному інтервалі I = [0, 1]. Інтерпретація чисел при співвідношенні всіх елементів множини тепер складніша. Звичайно, число 1 відповідає елементу, що належить множині B, а 0 означає, що елемент точно не належить множині B. Всі інші значення визначають ступінь приналежності до множини B. Для наочності приведемо характеристичну функцію множини молодих людей, як і в першому прикладі.
Рисунок 9.2 – Характеристична функція множини молодих людей
Хай E = {x1, x2, x3, x4, x5}, M = [0, 1 ]; A – нечітка множина, для якої µA(x1)=0,3; µA(x2)=0; µA(x3)=1; µA(x4)=0,5; µA(x5)=0,9 Тоді A можна представити у вигляді: A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } або A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5 (знак "+" є операцією не складання, а об'єднання) або
Формалізуємо неточне визначення «гарячий чай». Як x (область існування) виступатиме шкала температури в градусах Цельсія. Очевидно, що вона буде змінюється від 0 до 100 градусів. Нечітка множин
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.75.227 (0.16 с.) |
 (8.1)
(8.1) та
та  . (8.2)
. (8.2) (8.3)
(8.3) (8.4)
(8.4) (8.5)
(8.5) .
. , і отримаємо:
, і отримаємо: .
. , (8.6)
, (8.6) . Перший гравець діє за принципом
. Перший гравець діє за принципом  , тобто він мінімізує максимальний виграш другого гравця. Якщо позначити виграш другого гравця через w, то ми маємо:
, тобто він мінімізує максимальний виграш другого гравця. Якщо позначити виграш другого гравця через w, то ми маємо: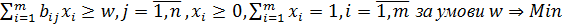 .
. , і отримаємо:
, і отримаємо: .
. , (8.7)
, (8.7) (8.8)
(8.8)

 ,
,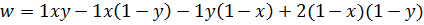

 . (8.9)
. (8.9) . (8.10)
. (8.10)