Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛЕКЦІЯ 3 «Статистична детермінована модель з дефіцитом»
Анотація Статична модель економічного замовлення з наявністю дефіциту запасів. Стохастичні моделі управління запасами. Стохастичні моделі управління запасами з фіксованим часом затримки поставок. 3.1 Статистична детермінована модель з дефіцитом В розглянутій моделі будемо вважати наявність дефіциту. Це означає, що при відсутності запасоємного продукту, тобто при J(t)=0 попит зберігається з тією ж інтенсивність r(t)=b, але споживання запасу відсутнє – b(t)=0, внаслідок чого накопичується дефіцит із швидкістю b. Графік зміни рівня запасу в цьому випадку представлений на рис. 3.1.
Рисунок3.1 – Графік зміни рівня запасу
Спадання графіку нижче осі абсцис в область від’ємних значень на відміну від графіка на рис 3.1 характеризує накопичення дефіциту. З рис.3.1 видно, що кожний період «пилки» Необхідність покриття дефіциту приводить до того, що максимальний рівень запасу s в момент надходження кожної партії тепер не дорівнює його об’єму n, а менше його на величину дефіциту n-s, накопиченого за час Т2 (див. рис.3.1). З геометричних міркувань легко встановити, що
В даній моделі в функцію сумарних затрат С поряд із затратами С1 (на поповнення запасу) та С2 (на зберігання запасу необхідно ввести затрати С3 – на штраф із-за дефіциту, тобто С=С1+С2+С3. Затрати С1, як і раніше, знаходимо за формулою (2.11). В попередньому розділі було показано, що затрати С2 при лінійних витратах запасу дорівнюють затратам на зберігання середнього запасу, який на час споживання Т1 дорівнює
При розрахунку затрат С3 будемо вважати, що штраф за дефіцит становить за одиницю часу с3 на кожну одиницю продукту. Так як середній рівень дефіциту за період Т2 дорівнює (n-s)T2/2, то штраф за цей період Т2 складає
Тепер, враховуючи (2.12), (3.2) та (3.3), сумарні затрати дорівнюють
Неважко помітити, що при n=s формула (3.3) співпадає з отриманою раніше (3.2) в моделі без дефіциту.
Розглянута задача управління запасами зводиться до відшукання такого об’єму партії n та максимального рівня запасу s, при яких функція С (2.16) приймає мінімальне значення. Іншими словами, необхідно дослідити функцію двох змінних C(n, s) на екстремум. Прирівнюючи часткові похідні
Вирішуючи систему, отримуємо формули найбільш економічного об’єму партії
Величина
називається щільністю збитків із-за незадоволеного попиту і відіграє важливу роль в управлінні запасами. Відмітимо, що Використовуючи (3.8), основні формули (3.6) і (3.7) можна записати компактніше:
Необхідно врахувати, що в силу (3.1) та (3.10) Із порівняння формул (3.9) та (2.10) випливає, що оптимальні об’єми партій для задач з дефіцитом та без дефіциту при однакових параметрах пов’язані співвідношенням
звідки випливає, що оптимальний об’єм партії в задачі з дефіцитом завжди більший (в Приклад 5. Знайти найбільш економічний об’єм партії та інтервал між поставками, зберігаючи умови задачі 2, окрім недопустимості дефіциту, якщо відомо, що відсутність на збірці кожної деталі приносить на добу збитки в розмірі 3,5 грош. од. Рішення. За умовою с3=3,5. Раніше за формулою (2.9) було отримано n0=4335 та за (2.15) Т0=13,2. Знайдемо щільність збитків із-за незадоволеного попиту за формулою (2.24): p=3,5/(0,35+3,5)=0,909, тобто 100(1-0,909)=9,1% часу між поставками деталі на збірці будуть відсутні. Тепер оптимальний розмір партії за формулою (3.11)
3.2 Стохастичні моделі управління запасами
Розглянемо стохастичні моделі управління запасами, в яких попит являється випадковим. Ц ей факт істотно відбивається на характері відповідних моделей та значно ускладнює їх аналіз, тому будемо розглядати найпростіші моделі. Припустимо, що попит r за інтервал часу Т являється випадковим і задано його закон (ряд) розподілу p(r) або щільність ймовірностей φ(r) (як правило функції p(r) та φ(r) оцінюються на основі дослідних або статистичних даних). Якщо попит r нижчий рівня запасу s, то придбання (зберігання, продаж) надлишку продукту потребує додаткових затрат c2 на одиницю продукту; навпаки, якщо попит r вище рівня запасу s, то це приводить до штрафу за дефіцит c3 на одиницю продукції. В якості функції сумарних витрат, що в стохастичних моделях являється випадковою величиною, розглядають її середнє значення або математичне очікування. В моделі, що розглядається, при дискретному випадковому попиті r, що має закон розподілення p(r), математичне очікування сумарних витрат має вигляд:
У виразі (3.12) перший доданок враховує витрати на придбання (зберігання) надлишку s-r одиниць продукту (при r ≤ s), а другий доданок – штраф за дефіцит на r-s одиниць продукту (при r > s). У випадку неперервного випадкового процесу, що задається щільністю ймовірностей φ(r), вираз C(s) прийме вигляд:
Задача управління запасами заключається в знаходженні такого запасу s, при якому математичне очікування сумарних витрат (2.28) та (2.29) приймають мінімальне значення. В роботах А. Кафмана та У. Черчмена доведено, що при дискретному випадковому процесі r вираз (2.28) мінімальний при запасі s0, що задовольняє нерівностям F(s0) < p < F(s0+1), (3.14)
а при непереривному випадковому процесі r вираз (2.29) мінімальний при значення s0, визначеному із рівняння F(s0) = p, (3.15) де F(s) = p(r < s) (3.16)
є функцією розподілення попиту r, F(s0) та F(s0 + 1) – її значення; p – щільність збитків через незадовільний попит, що встановлюється за (3.8). Отриманий запас s0 при безперервному попиті за даним значенням p може бути знайдений і графічно (рис. 3.2)
Рисунок 3.2 – Графічне представлення запасу s0 при безперервному попиті Задача 6. Підприємство закуповує агрегат із запасними блоками до нього. Ціна одного блоку дорівнює 5 грош. один. У випадку виходу агрегату із ладу через поломку блока, що відсутній в запасі, простій агрегату та терміну замовлення нового блоку до нього обійдеться в 100 грош. од. Експериментальне розподілення агрегатів за числом блоків, що потребували заміни, представлені в табл.3.1.
Таблиця 3.1— Експериментальне розподілення агрегатів за числом блоків, що потребували заміни
Необхідно встановити оптимальне число блоків, які потрібно придбати разом з агрегатом. Рішення. За умовою c2=5, c3=100. Розрахуємо щільність збитків через недостатність запасних блоків за формулою (2.24) p = 100 / (5 + 100)=0,952. Враховуючи (2.32), найдемо значення функції розподілення попиту (табл.3.2)
Таблиця 3.2 – Функції розподілення попиту
З таблиці очевидно, що оптимальний запас становить s0 =2, та як він задовольняє нерівності (2.30): F(2) < 0,952 < F(3). Задача 7. Розв’язати задачу 6 при умові безперервного випадкового процесу r, розподіленого за показниковим законом з функцією розподілення F(r)=1-e-λr при λ =0,98.
Рішення. Оптимальне число запасних блоків s0 знайдемо з рівняння (2.31):
В умовах моделі що розглядається, припустимо, що витрачання запасу відбувається безперервно з однаковою інтенсивністю. Таку ситуацію можна представити графічно (рис.3.3)
Рисунок 3.3 – Графік безперервного витрачання запасу з однаковою інтенсивністю
Рис.3.3, а відповідає випадку r ≤ s, коли попит не перевищує запас, а Рисунок2.5, б – випадок, попит перевищує запас, тобто r > s. Слід відмітити, що насправді графік J(t) представляє ступінчату ломану, показану на рис.2.5 пунктиром, але для дослідження моделі нам простіше розглядати J(t) у вигляді прямої, що згладжує цю ламану. Середній запас, відповідний рис. 3.3, а дорівнює
Середній запас, відповідний рис.3.3, б з урахуванням формули (3.1), в якій вважаємо n=r, складає
Середній дефіцит продукту за період Т2 для випадку, що відповідає рис.3.3, б з урахуванням (3.1), де n=r, дорівнює
Математичне очікування сумарних витрат складе:
А. Кафманом та У. Черчменом доведено, що в цьому випадку математичне очікування (3.20) мінімальне при запасі s0, що задовольняє нерівності
L(s0) < p < L(s0 +1) (3.21)
де p знову ж таки встановлюється за формулою (3.8):
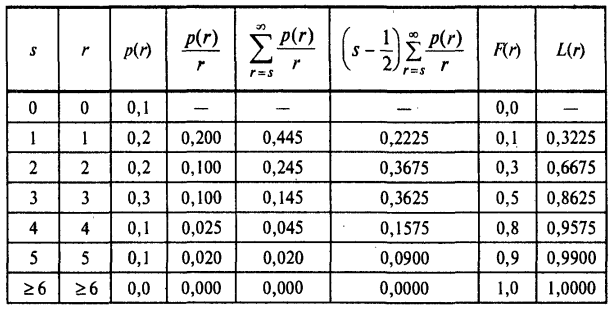
L(s0) та L(s0+1) – значення функції (2.38), а F(s) знаходиться у відповідності до визначення (3.16). Приклад 8. Вироби, що знаходяться на складі, рівномірно використовуються на протязі місяця. Затрати на зберігання одного виробу складають 5 грош. од., а штраф за дефіцит одного виробу обходиться в 100 грош. од. Вивчення попиту дало розподілення числа споживаних за місяць виробів, представлене в табл. 3.3. Таблиця 3.3 – Розподілення числа споживаних за місяць виробів
Необхідно, визначити оптимальний місячний запас складу. Рішення. Так же як і в задачі 6, с2=5, с3=100, p=0,952. Значення функції L(r) встановимо за допомогою таблиці 3.4.
Таблиця 3.4 – Алгоритм встановлення функції L(r)
Очевидно, що оптимальний запас виробів s0 = 3, так як він задовольняє умові (2.37): L(3) < 0,952 < L(4).
3.3 Стохастичні моделі управління запасами з фіксованим часом затримки поставок В розглянутих вище ідеалізованих моделях управляння запасами передбачалось, що поповнення запасів відбувається практично миттєво. Проте в багатьох задачах час затримки поставок може виявитись на стільки значним, що його необхідно враховувати в моделі.
Нехай за час затримок поставок Ө вже замовлено n партій по одній в кожний із n періодів тривалістю T=Ө/n. Позначимо: sнз – початковий рівень запасу (до початку першого періоду); si – запас за і -й період; ri – попит за і -й період; qi – поповнення запасу за і -й період. Тоді до кінця n- го періоду на склад поступить
або
де
Потрібно знайти оптимальний об’єм партії замовлення, який необхідно зробити за останній n -й період, попередній надходженню зробленого раніше замовлення. Математичне очікування сумарних витрат в цьому випадку встановлюється за формулою (3.12), а оптимальний запас s знаходиться за формулою (3.14), тобто
F(s0) < p < F(s0 +1) (3.27)
Знайшовши оптимальний запас s0 та знаючи q1, q2, …,qn-1, можна розрахувати qn за формулою (3.25), тобто
Завдання 9. Швидкопсувний товар що замовляється щоденно поступає в магазин через 7 днів після замовлення. В момент чергового замовлення запас товару склав 10 грош. од. Товар в день виготовлення приносить прибуток 0,95 грош. од., а не проданий в цей день товар може бути пізніше реалізований із збитками 0,10 грош.од. На основі експериментальних даних отримано наступне розподілення попиту на даний товар (табл. 3.5)
Таблиця 3.5 – Розпреділення попиту на товар
Необхідно встановити оптимальний об'єм замовляємого товару q7 на сьомий день після замовлення. Рішення. Щільність збитків через дефіцит товару за формулою (3.8) дорівнює p = 0,95 / (0,10 + 0,95) = 0,905. Враховуючи умови (3.16), знайдемо значення функції розподілення попиту (табл. 3.6)
Таблиця 3.6 – Значення функції розподілення попиту
Умову (3.27) задовольняють s0 =120 так як F(120) < 0,905 < F(130). Таким чином, оптимальний запас товару за 7 днів повинен бути на суму 120 грош. од., звідки оптимальний об’єм замовленого товару на сьомий день за (3.28) складе: q7 = 120 – (10 + (10 + 20 +10 + 10 + 20 +10)) = 30 грош. од.
|
||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.193.158 (0.068 с.) |
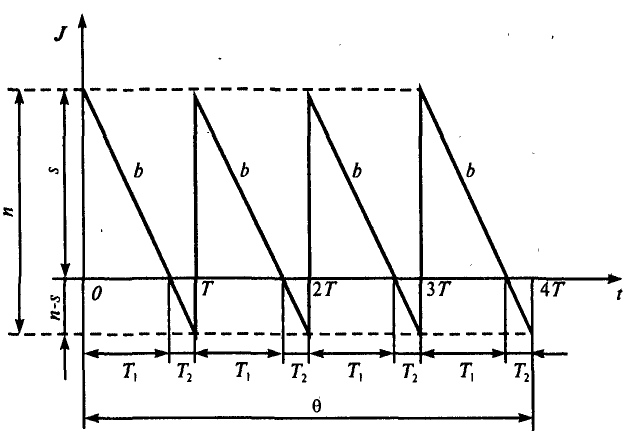
 розбиваються на два часових інтервали, тобто
розбиваються на два часових інтервали, тобто 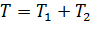 , де Т1 – час, на протязі якого відбувається споживання запасу, Т2 – час, коли запас відсутній та накопичується дефіцит, який буде перекритий в момент надходження наступної партії.
, де Т1 – час, на протязі якого відбувається споживання запасу, Т2 – час, коли запас відсутній та накопичується дефіцит, який буде перекритий в момент надходження наступної партії. (3.1)
(3.1) ; тому з урахуванням (2.7) та (2.5) ці затрати складають
; тому з урахуванням (2.7) та (2.5) ці затрати складають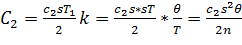 . (3.2)
. (3.2)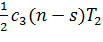 , а за весь період q з урахуванням (2.7) і (2.3) –
, а за весь період q з урахуванням (2.7) і (2.3) –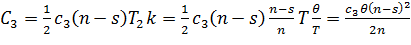 . (3.3)
. (3.3) . (3.4)
. (3.4)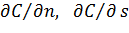 до нуля, отримаємо після перетворення систему рівнянь:
до нуля, отримаємо після перетворення систему рівнянь: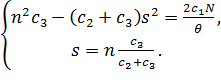 (3.5)
(3.5) та максимального рівня запасу
та максимального рівня запасу 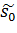 для моделі з дефіцитом:
для моделі з дефіцитом: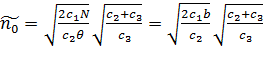 , (3.6)
, (3.6) . (3.7)
. (3.7)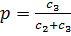 (3.8)
(3.8)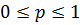 . Якщо значення c3 дорівнює з с2, то величина p наближається до нуля: коли с3 значно перевищує с2, то p близька до 1. Недопустимість дефіциту рівноцінна припущенню, що
. Якщо значення c3 дорівнює з с2, то величина p наближається до нуля: коли с3 значно перевищує с2, то p близька до 1. Недопустимість дефіциту рівноцінна припущенню, що 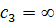 або p=1.
або p=1.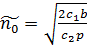 , (3.9)
, (3.9)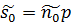 . (3.10)
. (3.10)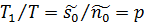 і
і 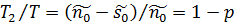 . Тому твердження про те, що щільність збитків із-за незадоволеного попиту дорівнює p, означає, що на протязі (1-p)100% часу від повного періоду Т запас продукту буде відсутній.
. Тому твердження про те, що щільність збитків із-за незадоволеного попиту дорівнює p, означає, що на протязі (1-p)100% часу від повного періоду Т запас продукту буде відсутній.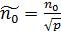 , (3.11)
, (3.11)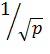 раз), ніж в задачі без дефіциту.
раз), ніж в задачі без дефіциту.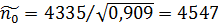 . В силу (2.15) пропорційно збільшено
. В силу (2.15) пропорційно збільшено  повинен збільшитись інтервал між поставками, тобто
повинен збільшитись інтервал між поставками, тобто днів.
днів.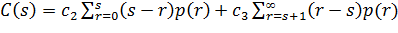 (3.12)
(3.12)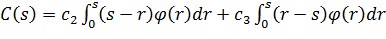 (3.13)
(3.13)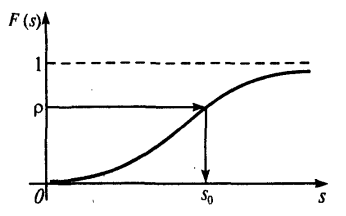


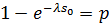 , звідки
, звідки 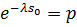 та
та 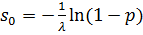 . При λ=0,98 s0 = -(1/0,98)ln0,02≈4 (блока).
. При λ=0,98 s0 = -(1/0,98)ln0,02≈4 (блока).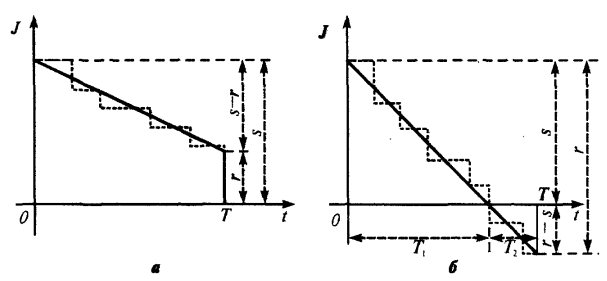
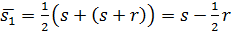 . (3.17)
. (3.17) (3.18)
(3.18)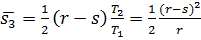 (3.19)
(3.19)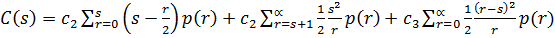 (3.20)
(3.20) (3.22)
(3.22)
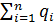 одиниць продукту, а витрачено буде
одиниць продукту, а витрачено буде 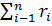 одиниць, тобто
одиниць, тобто , (3.23)
, (3.23)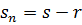 (3.24)
(3.24)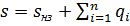 , (3.25)
, (3.25) . (3.26)
. (3.26) . (3.28)
. (3.28)