
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекція 1 «дослідження операцій як науковий підхід до аналізу економічних об’єктів»Стр 1 из 7Следующая ⇒
ЛЕКЦІЯ 9 «Нечіткі множини» Анотація Еволюція теорії нечітких множин. Поняття нечітких множин. Основні характеристики нечітких множин. Функція приналежності. Операції над нечіткими числами. Операції над нечіткими множинами. Наочне представлення операцій над нечіткими множинами. Переваги та застосування нечітких систем
9.1 Еволюція теорії нечітких множин Теорія множин – розділ математики, в якому вивчаються загальні властивості множин. Теорія множин лежить в основі більшості математичних дисциплін; вона зробила глибокий вплив на розуміння предмету самої математики. До другої половини XIX століття поняття «множини» не розглядалося як математичне («множина книг на полиці», «множина людських чеснот» і т. д. – все це чисто побутові обороти мови). Положення змінилося, коли німецький математик Георг Кантор розробив свою програму стандартизації математики, в рамках якої будь-який математичний об'єкт повинен був виявлятися тою або іншою «множиною». Наприклад, натуральне число, по Канторові, слід було розглядати як множину, що складається з єдиного елементу іншої множини, званої «натуральним рядом», – який, у свою чергу, сам є множиною, що задовольняє так званим аксіомам Пеано. Напевно, самою вражаючою людського інтелекту є здатність ухвалювати правильні рішення в умовах неповної і нечіткої інформації. Побудова моделей наближених роздумів людини і використання їх в комп'ютерних системах представляє сьогодні одну з найважливіших проблем науки. Основи нечіткої логіки були закладені в кінці 60-х років в роботах відомого американського математика Лотфі Заде. Дослідження такого роду було викликано зростаючим незадоволенням експертними системами. Хвалений "штучний інтелект", який легко справлявся із завданнями управління складними технічними комплексами, був безпорадним при простих висловах повсякденному життю, типу "Якщо в машині перед тобою сидить недосвідчений водій – тримайся від неї подалі". Для створення дійсно інтелектуальних систем, здатних адекватно взаємодіяти з людиною, був необхідний новий математичний апарат, який переводить неоднозначні життєві твердження в мову чітких і формальних математичних формул. Першим серйозним кроком в цьому напрямі стала теорія нечітких множин, розроблена Заді. Його робота "Fuzzy Sets", опублікована в 1965 році в журналі "Information and Control", заклала основи моделювання інтелектуальної діяльності людини і стала початковим поштовхом до розвитку нової математичної теорії. Він же дав і назву для нової області науки - "fuzzy logic" (fuzzy – нечіткий, розмитий, м'який). На відміну від булевої алгебри, у котрій існує лише дві величини (0 та 1, правда чи неправда) у нечіткій логіці існують також перехідні величини (стани).
Існує легенда про те, яким чином була створена теорія "нечітких множин". Одного разу Заде мав довгу дискусію зі своїм другом щодо того, чия з дружин привабливіша. Термін "приваблива" є невизначеним і в результаті дискусії вони не змогли прийти до задовільного підсумку. Це змусило Заде сформулювати концепцію, яка виражає нечіткі поняття типу "приваблива" в числовій формі. Подальші роботи професора Лотфі Заде і його послідовників заклали фундамент нової теорії і створили передумови для впровадження методів нечіткого управління в інженерну практику. Апарат теорії нечітких множин, продемонструвавши ряд багатообіцяючих можливостей застосування - від систем управління літальними апаратами до прогнозування підсумків виборів, виявився разом з тим складним для втілення. Враховуючи наявний рівень технології, нечітка логіка зайняла своє місце серед інших спеціальних наукових дисциплін - десь посередині між експертними системами і нейронними мережами. Тріумфальний хід нечіткої логіки по світу почався після доказу в кінці 80-х Бартоломеєм Косько знаменитої теореми FAT (Fuzzy Approximation Theorem). У бізнесі і фінансах нечітка логіка отримала визнання після того, як в 1988 році експертна система на основі нечітких правил для прогнозування фінансових індикаторів єдина передбачила біржовий крах. І кількість успішних фаззі-застосувань в даний час обчислюється тисячами. Третій період почався з кінця 80-х років і до цих пір. Цей період характеризується бумом практичного застосування теорії нечіткої логіки в різних сферах науки і техніки. До 90-го року з'явилося близько 40 патентів, що відносяться до нечіткої логіки (30 - японських). Сорок вісім японських компаній створюють лабораторію LIFE (Laboratory for International Fuzzy Engineering), японський уряд фінансує 5-річну програму по нечіткій логіці, яка включає 19 різних проектів, - від систем оцінки глобального забруднення атмосфери і передбачення землетрусів до АСОВІ заводських цехів. Результатом виконання цієї програми була поява цілого ряду нових масових мікрочіпів, що базуються на нечіткій логіці. Сьогодні їх можна знайти в пральних машинах і відеокамерах, цехах заводів і моторних відсіках автомобілів, в системах управління складськими роботами і бойовими вертольотами.
У США розвиток нечіткої логіки йде по шляху створення систем для великого бізнесу і військових. Нечітка логіка застосовується при аналізі нових ринків, біржовій грі, оцінки політичних рейтингів, виборі оптимальної цінової стратегії і тому подібне. З'явилися і комерційні системи масового застосування. Зсув центру досліджень нечітких систем у бік практичних застосувань привів до постановки цілого ряду проблем, зокрема: нова архітектура комп'ютерів для нечітких обчислень; елементна база нечітких комп'ютерів і контроллерів; інструментальні засоби розробки; інженерні методи розрахунку і розробки нечітких систем управління, і тому подібне. Основні зусилля кібернетики зараз направлені на створення штучного інтелекту, що не поступається людському мозку. Оскільки комп'ютери розуміють тільки мову математики, то виникла необхідність представлення нечітких понять у вигляді математичних змінних, названих лінгвістичними. Сукупність лінгвістичних змінних (мало, багато...) складає нечітка множина. Наприклад, вік (молодий + не молодий + старий + немолодий +.). Для опису нечітких множин вводяться поняття нечіткої і лінгвістичної змінних. Нечітка змінна описується набором (N,X,A), де N – це назва змінної, X – універсальна множина (область міркувань), A – нечітка множина на X. Значеннями лінгвістичної змінної можуть бути нечіткі змінні, тобто лінгвістична змінна знаходиться на більш високому рівні, чим нечітка змінна. Кожна лінгвістична змінна складається з: ¾ назви; ¾ множини своїх значень, яка також називається базовою терм–множиною T. Елементами базової терм-множини є назви нечітких змінних; ¾ універсальної множини X; ¾ синтаксичного правила G, за яким генеруються нові терми із застосуванням слів природної або формальної мови; ¾ семантичного правила P, яке кожному значенню лінгвістичної змінної ставить у відповідність нечітку підмножину множини X. Розглянемо таке нечітке поняття як «Ціна акції». Це і є назва лінгвістичною змінною. Сформуємо для неї базову терм-множину, яка складатиметься з трьох нечітких змінних: «Низька», «Помірна», «Висока» і задамо область міркувань у вигляді X=[100; 200] (одиниць). Останнє, що залишилося зробити – побудувати функції приналежності для кожного лінгвістичного терма з базового терм-множини T. Ступінь приналежності може трактуватися по різному в залежності від завдання, в якій використовується нечітка множина. Можливі трактування ступеня приналежності: ¾ ступінь відповідності поняттю А, ¾ ймовірність, ¾ можливість, ¾ корисність,
¾ істинність, ¾ правдоподібність, ¾ значення функції та ін. Для кожної трактування ступеня приналежності розроблені свої методи побудови функцій приналежності. У ряді моделей м'яких обчислень функції приналежності задаються досить довільно в параметричному вигляді. Наприклад, функції приналежності нечітких множин можуть спочатку задаватися в моделі так, щоб вони "рівномірно покривали" область визначення X, а потім налаштовуватися в результаті зміни їх параметрів в процесі налагодження моделі.
9.2 Поняття нечітких множин Хай E - універсальна множина, x - елемент E, а R – певна властивість. Звичайна (чітка) підмножина A універсальної множини E, елементи якої задовольняють властивість R, визначається як множина впорядкованої пари A = {µA (х) /х}, де µA(х) – характеристична функція, що приймає значення 1, коли x задовольняє властивості R, і 0 – в іншому випадку. Нечітка підмножина відрізняється від звичайної тим, що для елементів x з E немає однозначної відповіді "ні" щодо властивості R. У зв'язку з цим, нечітка підмножина A універсальної множини E визначається як множина впорядкованою парі A = {µA(х) /х}, де µA(х) - характеристична функція приналежності (або просто функція приналежності), що приймає значення в деякій впорядкованій множині M (наприклад, M = [0, 1]). Функція приналежності указує ступінь (або рівень) приналежності елементу x до підмножини A. Множину M називають множиною ознак. Якщо M = {0,1}, тоді нечітка підмножина A може розглядатися як звичайна або чітка множина. Розглянемо множину X всіх чисел від 0 до 10. Визначимо підмножину A множини X всіх дійсних чисел від 5 до 8. A = [5, 8] Покажемо функцію приналежності множині A, ця функція ставить у відповідність число 1 або 0 кожному елементу в X, залежно від того, належить даний елемент підмножині A чи ні. Результат представлений на рисунку 9.1.
Рисунок9.1 – Зображення приналежності звичайної (чіткої) множини
Можна інтерпретувати елементи, відповідні 1, як елементи, що знаходяться в множині A, а елементи, відповідні 0, як елементи, що не знаходяться у множині A. Ця концепція використовується в багатьох областях. Але існують ситуації, в яких даній концепції не вистачатиме гнучкості. У даному прикладі опишемо множину молодих людей. Формально можна записати так B = { множина молодих людей} Оскільки, взагалі, вік починається з 0, то нижня межа цієї множини повинна бути нулем. Верхню межу визначити складніше. Спочатку встановимо верхню межу, скажімо, рівну 20 рокам. Таким чином, маємо B як чітко обмежений інтервал, буквально: B = [0, 20]. Виникає питання: чому хтось в свій двадцятирічний ювілей – молодий, а відразу наступного дня вже не молодий? Очевидно, це структурна проблема, і якщо пересунути верхню межу в іншу точку, то можна поставити таке ж питання.
Природніший шлях створення множини B полягає в ослабленні строгого ділення на молодих і не молодих. Зробимо це, виносячи не тільки чіткі думки "Так, він належить множині молодих людей" чи ні, вона не належить множині молодих людей", але і гнучкі формулювання "Так, він належить до досить молодих людей" чи ні, він не дуже молодий". Розглянемо як за допомогою нечіткої множини визначити вираз "він ще молодий". У першому прикладі ми кодували всі елементи множини за допомогою 0 чи 1. Простим способом узагальнити дану концепцію є введення значень між 0 і 1. Реально можна навіть допустити нескінченне число значень між 0 і 1, в одиничному інтервалі I = [0, 1]. Інтерпретація чисел при співвідношенні всіх елементів множини тепер складніша. Звичайно, число 1 відповідає елементу, що належить множині B, а 0 означає, що елемент точно не належить множині B. Всі інші значення визначають ступінь приналежності до множини B. Для наочності приведемо характеристичну функцію множини молодих людей, як і в першому прикладі.
Рисунок 9.2 – Характеристична функція множини молодих людей
Хай E = {x1, x2, x3, x4, x5}, M = [0, 1 ]; A – нечітка множина, для якої µA(x1)=0,3; µA(x2)=0; µA(x3)=1; µA(x4)=0,5; µA(x5)=0,9 Тоді A можна представити у вигляді: A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } або A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5 (знак "+" є операцією не складання, а об'єднання) або
Формалізуємо неточне визначення «гарячий чай». Як x (область існування) виступатиме шкала температури в градусах Цельсія. Очевидно, що вона буде змінюється від 0 до 100 градусів. Нечітка множина для поняття «Гарячий чай» може виглядати таким чином: C = {0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70; 1/80; 1/90; 1/100}. Так, чай з температурою 60°С належить до множини «Гарячий» зі ступенем приналежності 0,80. Для однієї людини чай при температурі 60°С може опинитися гарячим, для іншого – не дуже гарячим. Саме у цьому і виявляється нечіткість завдання відповідної множини.
9.3 Основні характеристики нечітких множин Хай M = [0, 1] і A – нечітка множина з елементами з універсальної множина E і з множиною визначення M ¾ Величина µA(x) ¾ Нечітка множина є порожньою, якщо ∀ x ∈ E µA(x) = 0. Не порожню субнормальну множину можна нормалізувати за формулою µA(x):= ¾ Нечітка множина є унімодальною, якщо µA(x) = 1 лише для одного x з E. ¾ Носієм нечіткої множини A є звичайна підмножина з властивістю µA(x) >0, тобто носій A = {x/µA(x)>0} ∀ x ∈ E
¾ Елементи x ∈ E, для яких µA(x)=0,5 називаються точками переходу множини A.
Наведемо приклади нечітких множин з їх характеристиками: 1. Хай E = {0,1,2..,10}, M =[0, 1]. Нечітку множину "декілька" можна визначити таким чином: "декілька" = 0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8; її характеристики: – висота = 1, – носій = {3,4,5,6,7,8}, – точки переходу – {3,8}.
2. Хай E = {0,1,2,3...,n,...}. Нечітку множину "малий" можна визначити:
3. Хай E = {1,2,3...,100} і відповідає поняттю "вік", тоді нечітку множину "молодий", можна визначити з допомогою
Нечітка множина "молодий" на універсальній множині E’ ={ Іванов, Петров, Сидорів...} задається за допомогою функції приналежності µ"молодий"(x) на E = {1,2,3..100} (вік), що називається відносно E' функцією сумісності, при цьому: µ"молодий"(Сидорів)= µ"молодий"(x), де x – вік Сидорова.
4. Хай E = { Запорожець, Жигулі, Мерседес....} – множина марок автомобілів, а E' = [0,µ] – універсальна множина "вартість", тоді на E' ми можемо визначити нечітку множинe типу: "для небагатих", "для середнього класу", "престижні", з функціями приналежності типу:
Рисунок 9.3 – Характеристична функція множини вартість автомобіля для людей різного достатку
Маючи ці функції і знаючи ціни автомобілів з E в даний момент часу, визначимо на E' нечіткі множини з цими ж назвами. Так, наприклад, нечітка множина "для небагатих", задана на універсальній множині E = { Запорожець, Жигулі, Мерседес....} виглядає таким чином:
Рисунок 9.4 – Характеристична функція множини "для небагатих"
Аналогічно можна визначити нечітку множину "швидкісні", "середні", "тихохідні" і так далі.
9.4. Функція приналежності У приведених вище прикладах використані прямі методи, коли експерт або просто задає для будь-якого x ∈ E значення µA(x), або визначає функцію приналежності. Як правило, прямі методи завдання функції приналежності використовуються для вимірних понять, таких як швидкість, година, відстань, тиск, температура і так далі, тобто коли виділяються полярні значення. У багатьох завданнях при характеристиці об'єкту можна виділити набір ознак і для будь-якого з них визначити полярні значення, що відповідають значенням функції приналежності, 0 або 1. Наприклад, в завданні розпізнавання особи можна виділити наступні пункти:
Для конкретної особи А експерт, виходячи з приведеної шкали, задає µA(x) ∈ [0, 1], формуючи векторну функцію приналежності { µA(x1)), µA(x2)... µA(x9)}. Непрямі методи визначення значень функції приналежності використовуються у випадках, коли немає елементарних вимірних властивостей для визначення нечіткої множини. Як правило, це методи попарних порівнянь. Якби значення функцій приналежності були відомі, наприклад, µA(xi) = wi, i=1,2,...,n, тоді попарні порівняння можна представити матрицею відносин A = {aij}, де aij=wi / wj (операція ділення). Існує понад десяток типових форм кривих для завдання функцій приналежності. Найбільшого поширення набули: трикутна, трапецеїдальна функції та функція приналежності Гауса. Трикутна функція приналежності визначається трійкою чисел (а,b,c), і її значення в точці x обчислюється згідно виразу:
При (b - a) = (c - b) маємо випадок симетричної трикутної функції приналежності, яка може бути однозначно задана двома параметрами з трійки (а,b,c). Аналогічно для завдання трапецеїдальній функції приналежності необхідна четвірка чисел (а,b,c,d):
При (b - a) = (d - c) трапецеїдальна функція приналежності приймає симетричний вигляд.
a b Рисунок 9.5 – Типові кусочно-лінійні функції приналежності: трикутна (а) та трапецеїдальна (b).
Функція приналежності гауссова типу описується формулою
і оперує двома параметрами. Параметр с позначає центр нечіткої множини, а параметр σ відповідає за крутизну функції.
Рисунок 9.6 – Гауссова функція приналежності
Сукупність функцій приналежності для кожного терма з базової терм-множини T зазвичай зображаються разом на одному графіку. На рис. 9.7 приведений приклад описаної вище лінгвістичної змінної «Ціна акції», на рис. 9.8 – формалізація неточного поняття «Вік людини». Так, для людини 48 років ступінь приналежності до множини «Молодий» рівна 0, «Середній» – 0,47, «Вище середнього» – 0,20.
Рисунок 9.8 – Опис лінгвістичної змінної «Вік»
Кількість термів в лінгвістичній змінній рідко перевищує 7.
9.5 Операції над нечіткими числами Цілий розділ теорії нечітких множин – м'які обчислення (нечітка арифметика) – вводить набір операцій над нечіткими числами. Ці операції вводяться через операції над функціями приналежності на основі так званого сегментного принципу. Визначимо рівень приналежності α як ординату функції приналежності нечіткого числа. Тоді перетин функції приналежності з нечітким числом дає пару значень, які прийнято називати межами інтервалу достовірності. Задамося фіксованим рівнем приналежності α і визначимо відповідні йому інтервали достовірності по двох нечітких числах A і B: [a1, a2] і [b1, b2], відповідно. Тоді основні операції з нечіткими числами зводяться до операцій з їх інтервалами достовірності. А операції з інтервалами, у свою чергу, виражаються через операції з дійсними числами - межами інтервалів: ¾ операція "складання": [a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2] (9.6)
¾ операція "віднімання": [a1, a2] (-) [b1, b2] = [a1 - b2, a2 - b1] (9.7)
¾ операція "множення": [a1, a2] (×) [b1, b2] = [a1 × b1, a2 × b2], (9.8)
¾ операція "ділення": [a1, a2] (/) [b1, b2] = [a1 / b2, a2 / b1], (9.9)
¾ операція "піднесення до ступеня": [a1, a2] (^) i = [a1i, a2i]. (9.10)
З суті операцій з трапезоїдними числами можна зробити ряд важливих тверджень: ¾ дійсне число є окремим випадком трикутного нечіткого числа; ¾ сума трикутних чисел є трикутне число; ¾ трикутне (трапезоїдне) число, помножене на дійсне число, є трикутне (трапезоїдне) число; ¾ сума трапезоїдних чисел є трапезоїдне число; Аналізуючи властивості нелінійних операцій з нечіткими числами (наприклад, ділення), дослідники приходять до висновку, що форма функцій приналежності результуючих нечітких чисел часто близька до трикутної. Це дозволяє апроксимувати результат, приводячи його до трикутного вигляду. І, якщо приводимість в наявності, тоді операції з трикутними числами зводяться до операцій з абсцисами вершин їх функцій приналежності. Тобто, якщо ми вводимо опис трикутного числа набором абсцис вершин (a, b, c), то можна записати:
(a1, b1, c1) + (a2, b2, c2) ≡ (a1 + a2, b1 + b2, c1 + c2) (9.11)
Це – найпоширеніше правило м'яких обчислень.
9.6. Операції над нечіткими множинами 1. Домінування (Вміщення) Хай A і B - нечіткі множини на універсальній множині E. Говорять, що A міститься в B, якщо ∀ x ∈ E µA(x) < µB(x). (9.12) Позначення: A ⊂ B. Коли використовують термін "домінування", тобто у випадку якщо A ⊂ B, говорять, що B домінує A. 2. Рівність A і B рівні, якщо ∀ x ∈ E µA(x) = µB(x). (9.13) Позначення: A = B. 3. Доповнення Хай µ = [0, 1], A і B - нечіткі множини, задані на E. A і B доповнюють один одного, якщо ∀ x ∈ Ε µA(x)= 1 - µB(x). (9.14) Позначення: Очевидно, що Доповнення нечіткої множини А позначається символом А і визначається
Операція доповнення відповідає логічному запереченню. 4. Перетин Перетин А і В позначається A ∩ B і визначається
Перетин відповідає логічній зв'язці «і». A∩B – найменша нечітка підмножина, яка міститься одночасно в A і B:
µA∩B(x)= µin(µA(x), µB(x)). (9.17) 5. Об'єднання Об'єднання нечітких множин А і В (А + В)
Об'єднання відповідає логічній зв'язці «або». А ∪ В – найбільша нечітка підмножина, яка включає як А, так і В, з функцією приналежності: µA ∪ B(x)= µax(µA(x), µ B(x)). (9.19)
6. Різниця
µA - B(x)= µA ∩
7. Диз'юнктивна сума А⊕B = (А - B)∪(B - А) = (А ∩ µA - B(x) = max{[min{µA(x), 1 - µB(x)}]; [min{1 - µA(x), µB(x)}] } (9.21)
8. Добуток А і В позначається АВ і визначається
9. Піднесення до ступеня
10. Концентрація, частковий випадок піднесення до ступеня:
CON (A) = A2. (9.24) 11. Розтягування (розмивання):
DIL(A) = A0.5 . (9.25) Властивості операцій ∪ і ∩ Хай А, В, С - нечіткі множини, тоді виконуються наступні властивості: ¾ ¾ ¾ ¾ ¾ A ∪ ∅ = A, де ∅ - порожня множина, тобто µ∅(x) = 0 ∀ x ∈ E; ¾ A∩ ∅ = ∅; ¾ A ∩ E = A, де E - універсальна множина; ¾ A ∪ E = E; ¾ На відміну від чітких множин, для нечітких множин в загальному випадку: ¾ A∩ ¾ A∪ Приклади: Хай: A = 0,4/x1 + 0,2/x2+0/x3+1/x4; B = 0,7/x1+0,9/x2+0,1/x3+1/x4; C = 0,1/x1+1/x2+0,2/x3+0,9/x4. Тоді, для визначених вище перетворень маємо: 1. A ⊂ B, тобто A міститься в B або B домінує A, С не зрівняно ні з A, ні з B, тобто пари {A, С} і {В, С} – пари не домінуємих нечітких множин. 2. A ≠ B ≠ C. 3.
4. A∩B = 0,4/x1 + 0,2/x2 + 0/x3 + 1/x4. 5. А∪С = 0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4. 6. А - С = А∩ В - А = 7. А ⊕ В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.
9.7. Наочне представлення операцій над нечіткими множинами Для нечітких множин можна застосувати візуальне уявлення. Розглянемо прямокутну систему координат, на осі ординат якої відкладаються значення µA(x), на осі абсцис в довільному порядку розташовані елементи E. Якщо E за своєю природою впорядковано, то цей порядок бажано зберегти в розташуванні елементів на осі абсцис. Таке уявлення робить наочними прості операції над нечіткими множинами. Хай A нечіткий інтервал між 5 до 8 і B нечітке число близько 4, як показано на рис. 9.9.
Рисунок 9.9 – Наочне представлення нечіткого інтервалу А і нечіткого числа В
Проілюструємо нечітку множину між 5 і 8 «І» (AND) близько 4 (синя лінія на рис. 9.10.а). Нечітка множина між 5 і 8 «АБО» (OR) близько 4 показано на наступному рисунку (знову синя лінія на рис. 9.10.б).
а б Рисунок 9.10 – Наочне представлення операцій «І» (а) та «АБО» (б)
Рис.9.11 ілюструє операцію доповнення. Синя лінія - це ДОПОВНЕННЯ нечіткої множини A.
Рисунок 9.11 – Ілюстрація операції доповнення нечіткої множини А
На рис. 9.12 заштрихована частина відповідає нечіткій множині A і зображає область значень А і всіх нечітких множин, що містяться в A. Решта рисунків зображає відповідно,
Рисунок 9.12 – Наочне представлення операцій
На рис. 9.13 наведено наочний приклад використання операції концентрації та розмивання для нечіткої множини А.
Рисунок 9.13 – Операції концентрації CON(A) та розмивання DIL(A) 9.8. Переваги та застосування нечітких систем Коротко перерахуємо переваги fuzzy-систем в порівнянні з іншими: ¾ можливість оперувати нечіткими вхідними даними: наприклад, значення (динамічні завдання), що безперервно змінюються в часі, значення, які неможливо задати однозначно (результати статистичних опитів, рекламні компанії і так далі); ¾ можливість нечіткої формалізації критеріїв оцінки і порівняння: операція критеріями "більшість", "можливо", переважно" і т.д.; ¾ можливість проведення якісних оцінок як вхідних даних, так і вихідних результатів: ви оперуєте не тільки значеннями даних, але і їх мірою достовірності (не плутати з вірогідністю!) і її розподілом; ¾ можливість проведення швидкого моделювання складних динамічних систем і їх порівняльний аналіз із заданим ступенем точності: оперуючи принципами поведінки системи, описаними fuzzy-методами, ви по-перше, не витрачаєте багато часу на з'ясування точних значень змінних і складання рівнянь, що описують, по-друге, можете оцінити різні варіанти вихідних значень. Що стосується вітчизняного ринку комерційних систем на основі нечіткої логіки, то його формування почалося в середині 1995 року. Популярними є наступні пакети: • CubiCalc 2.0 RTC – одна з могутніх комерційних експертних систем на основі нечіткої логіки, що дозволяє створювати власні прикладні експертні системи; • CubiQuick – дешева "університетська" версія пакету CubiCalc; • RuleMaker – програма автоматичного витягання нечітких правил зі вхідних даних; • FuziCalc – електронна таблиця з нечіткими полями, що дозволяє робити швидкі оцінки при неточних даних без накопичення погрішності; • OWL – пакет, що містить початкові тексти всіх відомих видів нейронних мереж, нечіткій асоціативній пам'яті і так далі. Основними споживачами нечіткої логіки на ринку СНД є банкіри і фінансисти, а також фахівці в області політичного і економічного аналізу. Вони використовують CubiCalc для створення моделей різних економічних, політичних, біржових ситуацій. Що ж до пакету FuziCalc, то він зайняв своє місце на комп'ютерах великих банкірів і фахівців з надзвичайних ситуацій – тобто тих, для кого важлива швидкість проведення розрахунків в умовах неповноти і неточності вхідної інформації. Проте можна з упевненістю сказати, що епоха розквіту прикладного використання нечіткої логіки на вітчизняному ринку ще попереду. Сьогодні елементи нечіткої логіки можна знайти в десятках промислових виробів – від систем управління електропоїздами і бойовими вертольотами до пилососів і пральних машин. Без застосування нечіткої логіки немислимі сучасні ситуаційні центри керівників західних країн, де ухвалюються ключові політичні рішення і моделюються різні кризові ситуації. Одним з вражаючих прикладів масштабного застосування нечіткої логіки стало комплексне моделювання системи охорони здоров'я і соціального забезпечення Великобританії (National Health Service – NHS), яке вперше дозволило точно оцінити і оптимізувати витрати на соціальні потреби. Не обійшли засоби нечіткої логіки і програмні системи, обслуговуючих великий бізнес. Першими, зрозуміло, були фінансисти, завдання яких вимагають щоденного ухвалення правильних рішень в складних умовах непередбаченого ринку. Перший рік використання системи Fuji Bank приніс банку в середньому $770000 на місяць (і це тільки офіційно оголошений прибуток!). Услід за фінансистами, стурбовані успіхами японців і втратою стратегічної ініціативи, когнітивними нечіткими схемами зацікавилися промислові гіганти США. Motorola, General Electric, Otis Elevator, Pacific Gas & Electric, Ford та інші на початку 90-х почали інвестувати в розробку виробів, що використовикористовують нечітку логіку. Маючи солідну фінансову "підтримку", фірми, що спеціалізуються на нечіткій логіці, дістали можливість адаптувати свої розробки для широкого круга застосувань. "Зброя еліти" вийшла на масовий ринок. Серед лідерів нового ринку виділяється американська компанія Hyper Logic, заснована в 1987 році Фредом Уоткинсом (Fred Watkins). Спочатку компанія спеціалізувалася на нейронних мережах, проте незабаром цілком концентрувалася на нечіткій логіці. Недавно вийшла на ринок друга версія пакету CubiCalc фірми HyperLogic, яка є одній з щонайпотужніших експертних систем на основі нечіткої логіки. Пакет містить інтерактивну оболонку для розробки нечітких експертних систем і систем управління, а також run-time модуль, що дозволяє оформляти створені користувачем системи у вигляді окремих програм. Окрім Hyper Logic серед "патріархів" нечіткої логіки можна назвати фірми IntelligenceWare, InfraLogic, Aptronix. Всього ж на світовому ринку представлено більше 100 пакетів, які так чи інакше використовують нечітку логіку. У трьох десятках СУБД реалізована функція нечіткого пошуку. Власні програми на основі нечіткої логіки анонсували такі гіганти як IBM, Oracle та інші. На принципах нечіткої логіки створений і один з російських програмних продуктів – відомий пакет "Бізнес-прогноз". Призначення цього пакету – оцінка ризиків і потенційної прибутковості різних бізнес-планів, інвестиційних проектів і просто ідей щодо розвитку бізнесу. "Ведучи" користувача за сценарієм його задуму, програма задає ряд питань, які допускають як точні кількісні відповіді, так і наближені якісні оцінки, – типу "маловірогідно", "ступінь риски високий" і так далі Узагальнивши всю отриману інформацію у вигляді однієї схеми бізнеспроекта, програма не тільки виносить остаточний вердикт про ризиковану проекту і очікуваних прибутків, але і указує критичні крапки і слабкі місця в авторському задумі. Від аналогічних іноземних пакетів "Бізнес-прогноз" відрізняється простотою, дешевизною і, зрозуміло, російськомовним інтерфейсом. Втім, програма "Бізнес-прогноз" - лише перша ластівка, за якою неминуче з'являться нові розробки учених СНД.
ЛЕКЦІЯ 10 «Нечіткі множини в системах керування» Анотація Нечіткі моделі та системи. Поняття системи нечіткого логічного висновку. Основні етапи нечіткого виводу: формування бази правил, фазифікація вхідних змінних, агрегування підумов, активізація під висновків, акумуляція висновків, дефазифікація. Основні алгоритми нечіткого виводу. Приклади використання системи нечіткого виведення в задачах управління 10.1 Нечіткі моделі та системи Моделі статичних і динамічних систем, побудова, використання та аналіз яких базується на положеннях теорії нечітких множин і нечіткої логіки називають нечіткими моделями або нечіткими системами. Метою нечіткого моделювання складних явищ є наближений опис залежності (апроксимація деякої функції)
Y = f(X), де Y - вихідна лінгвістична змінна; Х - вектор вхідних лінгвістичних змінних розмірністю n; f - залежність між Х і Y, описувана сукупністю нечітких продукційних правил. Нечіткі моделі представляють узагальнення інтервально-оцінюваних моделей, які, в свою чергу, є узагальненням чітких моделей.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.159.224 (0.246 с.) |



 називається висотою нечіткої множини A. Нечітка множина A є нормальною, якщо її висота дорівнює 1, тобто верхня межа її функції приналежності дорівнює 1 (
називається висотою нечіткої множини A. Нечітка множина A є нормальною, якщо її висота дорівнює 1, тобто верхня межа її функції приналежності дорівнює 1 ( µA(x) = 1). При µA(x) < 1 нечітка множина називається субнормальною.
µA(x) = 1). При µA(x) < 1 нечітка множина називається субнормальною.
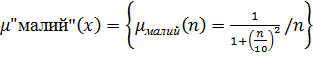 (9.1)
(9.1) (9.2)
(9.2)




 , (9.3)
, (9.3) , (9.4)
, (9.4)
 , (9.5)
, (9.5)


 або
або 
 =A. (Доповнення визначене для µ = [0, 1], але очевидно, що його можна визначити для будь-якого впорядкованого M).
=A. (Доповнення визначене для µ = [0, 1], але очевидно, що його можна визначити для будь-якого впорядкованого M). . (9.15)
. (9.15) . (9.16)
. (9.16) . (9.18)
. (9.18)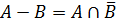 з функцією приналежності:
з функцією приналежності: (x) = min(µA(x), 1 - µB(x)). (9.20)
(x) = min(µA(x), 1 - µB(x)). (9.20) (9.22)
(9.22) (9.23)
(9.23) – комутативність;
– комутативність; – асоціативність;
– асоціативність; – ідемпотентність;
– ідемпотентність; - дистрибутивність;
- дистрибутивність; – теореми де Моргана.
– теореми де Моргана.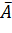 ≠ ∅,
≠ ∅, = 0,6/x1 + 0,8/x2 + 1/x3 + 0/x4;
= 0,6/x1 + 0,8/x2 + 1/x3 + 0/x4; = 0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4.
= 0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4.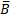 = 0,3/x1 + 0,1/x2 + 0/x3 + 0/x4;
= 0,3/x1 + 0,1/x2 + 0/x3 + 0/x4;












