Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение аэродинамических сил и моментовСодержание книги Поиск на нашем сайте
По известным распределениям давления И касательного напряжения
 и касательная к площадке сила и касательная к площадке сила 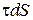 (рис. 10.1). Сумма проекций этих сил на ось ОX поточной системы координат равна (рис. 10.1). Сумма проекций этих сил на ось ОX поточной системы координат равна
где n – нормаль; t – касательная к площадке dS. Проекции от действия этих напряжений на оси ОY и ОZ можно записать аналогично. Чтобы получить суммарные силы, необходимо проинтегрировать по всей поверхности S. Введем коэффициент давления После подстановок получим в обозначениях для скоростной системы координат следующие интегральные выражения для проекций аэродинамической силы:
Интегралы в формулах (10.4) представляют собой безразмерные величины, учитывающие влияние на аэродинамические силы характера обтекания тела заданной геометрической формы и распределения безразмерных коэффициентов давления и трения по его поверхности. Их обозначают
Подобным образом получаются и общие соотношения для моментов:
где L – характерный геометрический размер (плечо силы); Анализ выражений для аэродинамических сил (10.4) показывает, что каждую из этих сил можно представить в виде суммы двух составляющих: – первая из них обусловлена аэродинамическим давлением (присуща как идеальной, так и реальной жидкости); – вторая обусловлена касательными напряжениями (присуща только для реальной, вязкой жидкости). Тогда, например, подъемную силу можно представить в виде суммы:
где
Или в коэффициентах:
Аналогично из двух составляющих можно представить лобовое сопротивление: В случае симметричного обтекания (a = 0) силы, обусловленные трением и давлением, с противоположных сторон тела взаимно компенсируются, и подъемная сила равна нулю. Поэтому подъемная сила появляется только в случае, когда a ¹0. Составляющие аэродинамических сил и моментов, зависящие от трения, не всегда по порядку величин такие же, как составляющие от давления. Влияние трения оказывается существенным при обтекании длинных и тонких тел, и в практических случаях влияние трения наиболее существенно для определения силы лобового сопротивления или продольной силы.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.70 (0.008 с.) |

 Пусть при некоторых углах атаки aи скольжения b, а также заданных параметрах набегающего потока (
Пусть при некоторых углах атаки aи скольжения b, а также заданных параметрах набегающего потока ( ,
,  ,
,  ,
,  ) известны распределения давления
) известны распределения давления 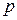 и касательных напряжений
и касательных напряжений  по поверхности обтекаемого тела. Требуется определить суммарные величины составляющих аэродинамической силы и момента.
по поверхности обтекаемого тела. Требуется определить суммарные величины составляющих аэродинамической силы и момента. ,
, , местный коэффициент трения
, местный коэффициент трения  и характерную площадь
и характерную площадь  (площадь крыла, миделя и др.).
(площадь крыла, миделя и др.). ,
, , (10.4)
, (10.4) .
. ,
,  и
и  – коэффициенты силы лобового сопротивления, подъемной силы и боковой силы. То есть
– коэффициенты силы лобового сопротивления, подъемной силы и боковой силы. То есть .
. ,
, – коэффициент момента крена;
– коэффициент момента крена; 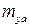 – коэффициент момента рыскания;
– коэффициент момента рыскания;  – коэффициент момента тангажа. Аналогично можно вывести соотношения для коэффициентов сил и моментов в связанной системе координат.
– коэффициент момента тангажа. Аналогично можно вывести соотношения для коэффициентов сил и моментов в связанной системе координат. ,
, – подъемная сила, обусловленная аэродинамическим давлением;
– подъемная сила, обусловленная аэродинамическим давлением; 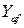 – подъемная сила, обусловленная трением.
– подъемная сила, обусловленная трением. .
. , где
, где  – сопротивление давления;
– сопротивление давления;  – сопротивление трения. Или для коэффициента лобового сопротивления:
– сопротивление трения. Или для коэффициента лобового сопротивления: