
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №5. Решение дифференциальных уравнений высших порядковСодержание книги
Поиск на нашем сайте
Цель занятия: знать типы дифференциальных уравнений высших порядков, допускающих понижение порядка; уметь понижать порядок каждого из этих уравнений; находить решение этих уравнений; воспитание самостоятельных навыков работы, организованности, целеустремленности.
Учебные вопросы
1. Решение дифференциальных уравнений высших порядков, допускающих понижение порядка. 2. Решение физических задач, приводящих к дифференциальным уравнениям высших порядков.
Ход занятия
Студенты должны знать ответы на вопросы: 1. Типы дифференциальных уравнений высшего порядка, допускающие понижение порядка 2. Методы понижения порядка каждого из этих типов. Основные рабочие формулы
I тип уравнения
Общее решение уравнения (1):
II тип уравнения
Подстановка:
III тип уравнения
Подстановка:
Решение дифференциальных уравнений высших порядков, допускающих понижение порядка
Задача 1. Найти общее решение уравнения: Решение.
2) Найдем частное решение. Подставим начальные условия в полученное общее решение. Получим:
Подставив в общее решение значения постоянных, получим частное решение:
Ответ:
Решить самостоятельно по образцу задачи 1. Найти общее решение уравнений: Задача 2. Задача 3.
Решить уравнения по образцу занятия 4 (задача 7). Задача 4. Задача 5.
Решить уравнения по образцу занятия 4 (задача 4). Задача 6. Задача 7.
Занятие №6. Решение линейных дифференциальных уравнений с постоянными коэффициентами
Цель занятия: усвоить навыки решения типовых линейных дифференциальных уравнений с постоянными коэффициентами; воспитание навыков самостоятельной деятельности, целеустремленности, организованности. Учебные вопросы
1. Решение линейных дифференциальных уравнений с постоянными коэффициентами.
Ход занятия
Студенты должны ответить на теоретические вопросы: 1. Определение линейного однородного уравнения п -го порядка с постоянными коэффициентами. 2. Понятие характеристического уравнения и методы его решения (вспомнить понятие дискриминанта и нахождение корней квадратного уравнения).
3. Формулы нахождения общего решения линейного однородного дифференциального уравнения в зависимости от корней характеристического уравнения. Рабочие формулы
1. Линейное однородное уравнение второго порядка с постоянными коэффициентами:
2. Характеристическое уравнение:
3. Если корни характеристического уравнения действительны и различны
Общее решение записывается в виде:
4. Корни характеристического уравнения действительные и равные, т.е.
Общее решение в этом случае:
5. Корни характеристического уравнения комплексные:
частные решения:
Общее решение уравнения (1) имеет вид:
Задача 1. Найти общее решение уравнения: Решение. 1. Составим характеристическое уравнение: 2. Решаем алгебраическое квадратное уравнение. Получим корни: 3. Т.к. корни действительные и различные, решение имеем в виде (3):
Ответ:
Задача 2. Решить самостоятельно по образцу задачи 1. Найти общее решение уравнения: Задача 3. Найти общее решение уравнения: Решение. 1) Составим характеристическое уравнение 2) По формуле (4) общее решение имеет вид:
Ответ:
Задача 4. Решить самостоятельно по образцу задачи 3. Найти общее решение уравнения:
Задача 5. Найти общее решение уравнения: Решение. 1) Составляем характеристическое уравнение 2) Общее решение по формуле (5) записывается:
частные решения:
где Ответ:
Задача 6. Решить самостоятельно по образцу задачи 5. Найти общее решение уравнения:
Задание для самостоятельной работы
Решить уравнения: Задача 7. Задача 8. Задача 9. Задача 10. Задача 11. Задача 12. Задача 13. Задача 14. Задача 15. Задача 16. Задача 17. Задача 18. Задача 19. Задача 20. Задача 21. Задача 22.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.78.182 (0.009 с.) |







 и частное решение с начальными условиями:
и частное решение с начальными условиями:  при
при  .
. (см. занятие 4, задача 1);
(см. занятие 4, задача 1);
 взять по ч
взять по ч  ;
;
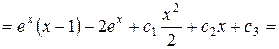
 общее решение уравнения.
общее решение уравнения.

 .
.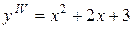 .
. .
. .
. .
. .
.

 , то частные решения:
, то частные решения: и
и 

 , частные решения:
, частные решения: и
и  .
.
 ;
; ;
; ;
; .
.
 .
. .
. .
. частные решения
частные решения общее решение.
общее решение.
 .
.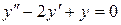 .
. , оно имеет двукратный корень
, оно имеет двукратный корень  .
.
 .
. .
. , которое имеет корни:
, которое имеет корни:  .
. ,
, ,
, ,
, .
.
 .
.


















