
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №1. Решение дифференциальных уравнений с разделяющимися переменнымиСодержание книги
Поиск на нашем сайте
Цель занятия: усвоить новые учебные элементы на уровне умения решать типовые дифференциальные уравнения с разделяющимися переменными; воспитание самостоятельных навыков учебной деятельности, трудолюбия.
Учебные вопросы
1. Решение дифференциальных уравнений с разделенными и разделяющимися переменными. 2. Решение физических и геометрических задач, приводящих к дифференциальным уравнениям с разделяющимися переменными.
Ход занятия
Студенты должны предварительно подготовить теоретический материал лекции к данному практическому занятию по вопросам: 1. Понятие дифференциального уравнения первого порядка. 2. Общее решение дифференциального уравнения. 3. Частное решение, геометрическая иллюстрация. 4. Определение уравнения с разделенными переменными, его запись. 5. Понятие уравнения с разделяющимися переменными и его запись в общем виде. 6. Алгоритм решения дифференциального уравнения с разделенными и разделяющимися переменными.
Основные рабочие формулы
1) Дифференциальное уравнение с разделенными переменными:
общее решение:
2) Дифференциальное уравнение с разделяющимися переменными:
Приведение к виду (1) с разделенными переменными:
где
1. Решение дифференциальных уравнений с разделенными и разделяющимися переменными
Задача 1. Решить дифференциальное уравнение: Решение. 1) Определяем тип дифференциального уравнения – с разделяющимися переменными. 2) Разделяем переменные, умножив обе части уравнения на один и тот же множитель:
Получим уравнение типа (1): 3) Решаем его, интегрируя обе части равенства:
4) Находим общее решение:
5) Находим постоянную интегрирования, подставив в общее решение начальные условия:
6) Находим частное решение, подставив значение постоянной интегрирования в общее решение:
Геометрически это совокупность (множество) точек
Задача 2. Решить самостоятельно по образцу задачи 1. Решить дифференциальное уравнение: а) найти общее решение: б) построить несколько интегральных кривых;
в) найти частный интеграл по начальным условиям: Указание. Переписать уравнение, подставив
Задача 3. Решить уравнение: Задание то же, что и в предыдущем примере, начальные условия:
Задача 4. Найти общее решение уравнения:
Задача 5. Найти общее и частное решения уравнения:
Задача 6. Решить уравнения: 1) 2)
2. Решение физических и геометрических задач, приводящих к дифференциальным уравнениям с разделяющимися переменными
Задача 7. Скорость точки равна Решение. 1) Известно,
2) Подставим выражение скорости: 3) Решаем дифференциальное уравнение с разделенными переменными:
4) Так как в начале движения 5) Находим путь, пройденный точкой за
Ответ:
Задача 9. Решить самостоятельно по образцу задачи 7. Скорость точки равна
Задача 10. Найти кривую, проходящую через т. Решение. Пусть
угловой коэффициент касательной к кривой в т.
Это и есть дифференциальное уравнение искомой кривой: Это уравнение с разделяющимися переменными. Разделяем переменные:
Используя начальные условия, найдем: Тогда искомая кривая
Рис. 1 Ответ:
Задание для самостоятельной работы
Задача 11. Задание аналогично задаче 2:
Решить уравнения: Задача 12.
Задача 13. Задача 14. Задача 15. Задача 16. Задача 17. Задача 18. Задача 19. Задача 20.
Вопросы для студентов
1. Объяснить алгоритм решения дифференциального уравнения, предложенного преподавателем из данного задания. 2. Ответить на теоретические вопросы, указанные в начале данного занятия. 3. Составить самостоятельно дифференциальное уравнение с разделяющимися переменными и решить его.
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.21.237 (0.007 с.) |


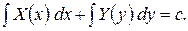




 удовлетворяющее начальным условиям:
удовлетворяющее начальным условиям: 








 , лежащих на гиперболе
, лежащих на гиперболе  . Интегральная кривая – гипербола, проходящая через точку с координатами
. Интегральная кривая – гипербола, проходящая через точку с координатами  .
. .
. .
. .
. .
. .
. .
. при
при  .
. ;
; .
. м/сек. Найти путь
м/сек. Найти путь  , пройденный точкой за промежуток времени
, пройденный точкой за промежуток времени  сек от начала движения.
сек от начала движения. для
для  , тогда в нашем случае:
, тогда в нашем случае: .
. .
. .
. , то при
, то при 
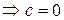 ; Тогда
; Тогда  .
. (м).
(м). м.
м. м/сек. Найти путь, пройденный точкой за время
м/сек. Найти путь, пройденный точкой за время  , для которой отрезок любой ее касательной, заключенной между координатными осями делится пополам в точке касания.
, для которой отрезок любой ее касательной, заключенной между координатными осями делится пополам в точке касания. есть середина касательной
есть середина касательной  , по условию являющаяся точкой касания (рис. 1). В силу условия:
, по условию являющаяся точкой касания (рис. 1). В силу условия:
 равен
равен  и равен:
и равен: .
. .
.
 .
. . Эта гипербола:
. Эта гипербола: 

 .
. .
. .
. ;
; ;
; ;
; ;
; ;
; ;
; .
.


