
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №7. Отыскание методом неопределенных коэффициентов частных решений неоднородных дифференциальных уравнений с правой частью специального вида ⇐ ПредыдущаяСтр 6 из 6
Цель занятия: усвоить навыки решения неоднородных дифференциальных уравнений с правой частью специального вида методом неопределенных коэффициентов; воспитание навыков самостоятельной работы, целеустремленности, организованности. Учебные вопросы
1. Решение линейных дифференциальных уравнений с правой частью специального вида:
2. Решение линейных уравнений с правой частью специального вида:
Ход занятия
Студенты должны ответить на вопросы лекции: 1) Алгоритм решения неоднородного линейного дифференциального уравнения второго порядка с правой частью специального вида 1. 2) Алгоритм решения неоднородного линейного дифференциального уравнения второго порядка с правой частью специального вида 2.
Рабочие формулы
Общее решение неоднородного уравнения
представляется как сумма частного решения этого уравнения
Общее решение уравнения (1):
Нахождению общего решения 1) Для линейных неоднородных дифференциальных уравнений второго порядка с правой частью специального вида:
частное решение ищется в виде:
где r – кратность корня характеристического уравнения, если 2) Для линейного неоднородного дифференциального уравнения второго порядка с правой частью специального вида:
частное решение ищется в виде:
где
Алгоритм решения неоднородных дифференциальных уравнений со специальной правой частью
1. Определить, что данное уравнение имеет вид:
2. Составить и решить характеристическое уравнение. 3. Записать общее решение однородного дифференциального уравнения
4. По виду правой части:
определить, является ли 5. Записать частное решение в виде (5) или (7) соответственно. 6. Найти 7. Записать общее решение неоднородного дифференциального уравнения по формуле:
1. Решение линейного неоднородного дифференциального уравнения с правой частью специального вида: Задача 1. Найти решение уравнения: Решение. 1) Общее решение ищем в виде (3). 2) Составляем характеристическое уравнение однородного дифференциального уравнения
которое имеет кратные корни 3) Общее решение однородного уравнения:
4) Находим частное решение неоднородного уравнения. Так как в правой части отсутствует
а именно в виде многочлена того же порядка, что и многочлен в правой части заданного уравнения. 5) Подставляем составленное частное решение в исходное уравнение, предварительно найдем:
Тогда Находим коэффициенты А и В, приравнивая коэффициенты в обеих частях равенства при одинаковых степенях х:
6) Подставляем полученные коэффициенты в частное решение
7) Находим общее решение по формуле (3), подставив найденные решения
Ответ:
Задача 2. Решить самостоятельно уравнение по образцу задачи 1:
Задача 3. Найти решение уравнения: Решение. 1) Найдем решение однородного уравнения:
2) Частное решение искомого уравнения составляется по виду правой части. В правой части многочлен нулевой степени, а именно:
Тогда:
3) Подставим полученные выражения
4) Общее решение искомого уравнения:
Ответ:
Задача 4. Решить самостоятельно уравнение по образцу задачи 3:
2. Решение линейного неоднородного дифференциального уравнения с правой частью специального вида:
Задача 5. Найти решение уравнения: Решение. 1) Ищем решение однородного уравнения:
2) Общее решение однородного уравнения:
3) Частное решение исходного уравнения. Так как в правой части этого уравнения отсутствует Так как такого корня нет среди корней характеристического уравнения (сравним
где А и В – многочлены нулевой степени. 4) Находим
5) Подставим полученные выражения
6) Приравнивая коэффициенты при
т.к. в правой части отсутствует член с
7) Частное решение:
8) Находим общее решение:
Ответ:
Задача 6. Решить самостоятельно уравнение по образцу задачи 5:
Задание для самостоятельной работы
Решить уравнения: Задача 7. Задача 8. Задача 9. Задача 10. Задача 11. Задача 12. Задача 13.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.181.209 (0.036 с.) |
 .
. .
.
 и общего решения
и общего решения  соответствующего однородного уравнения
соответствующего однородного уравнения

 уравнения (1).
уравнения (1).

 является его корнем (если
является его корнем (если  ),
), 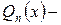 полный многочлен п -ой степени с неопределенными коэффициентами.
полный многочлен п -ой степени с неопределенными коэффициентами.

 кратность корня характеристического уравнения, если
кратность корня характеристического уравнения, если 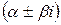 является корнем этого уравнения (если
является корнем этого уравнения (если  и
и  полные многочлены степени е с неопределенными коэффициентами, где
полные многочлены степени е с неопределенными коэффициентами, где 
 .
.

 .
. .
.
 ,
, .
. .
. , то
, то  , а число
, а число  ,
,


 .
.

 .
. .
. для этого решаем характеристическое уравнение:
для этого решаем характеристическое уравнение: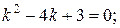
 .
. общее решение однородного уравнения.
общее решение однородного уравнения. По показателю
По показателю 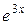 находим
находим  что является однократным корнем характеристического уравнения, следовательно,
что является однократным корнем характеристического уравнения, следовательно,  в формуле (5). Поэтому частное решение ищем в виде:
в формуле (5). Поэтому частное решение ищем в виде:


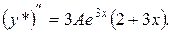
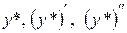 в исходное уравнение и найдем А:
в исходное уравнение и найдем А:










 характеристическое уравнение,
характеристическое уравнение, корни этого уравнения.
корни этого уравнения.
 , следовательно:
, следовательно:  .
. ), то в формуле (7)
), то в формуле (7)  стоит многочлен нулевой степени:
стоит многочлен нулевой степени:  Следовательно, частное решение исходного уравнения ищем в виде:
Следовательно, частное решение исходного уравнения ищем в виде:
 и
и  :
: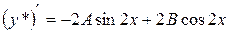 ;
; .
. в искомое уравнение, получим:
в искомое уравнение, получим: .
. в обеих частях равенства, получим:
в обеих частях равенства, получим:
 .
.


 .
. .
. .
. .
. .
.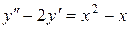 .
. .
.


