
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особые решения ДУ-1-ПРОП. Способы их отыскания.
Особое решение – решение, содержащее континуум особых точек. Чтобы найти кривые, подозрительные на особое решение, надо найти геометрическое место точек, в которых не действует теорема Коши-Пикара. Если они образуют одну или несколько кривых, то это – кривые, подозрительные на особое решение. Проверка кривой 1) проверить, является ли она решением 2) # # # ДУ 1 порядка с разделяющимися переменными и приводимые к ним. I. Теорема: пусть в области Доказательство: для любой точки из Если II. Теорема: пусть в области Доказательство: Если III. Такое уравнение решается аналогично предыдущему, но IV. Замена Иногда уравнение приводится к уравнению с разделяющимися переменными некоторой заменой Однородные ДУ 1 порядка
Уравнение Функция Свойства однородного уравнения: 1) Для 2) Точка 3) Изоклины – прямые, проходящие через 4) ИК симметричны относительно Теорема: однородное уравнение для Доказательство:
Иногда удобнее делать замену
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.152.173 (0.006 с.) |
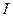 , подозрительной на особое решение:
, подозрительной на особое решение: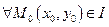 подставляем в общий интеграл
подставляем в общий интеграл 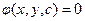 . Разрешаем это соотношение относительно
. Разрешаем это соотношение относительно  . Возможны три случая:
. Возможны три случая: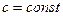 , тогда
, тогда 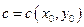 , тогда
, тогда 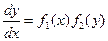
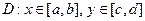
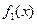 и
и 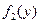 определены и непрерывны,
определены и непрерывны,  , тогда общий интеграл дается квадратурой
, тогда общий интеграл дается квадратурой  и задача Коши
и задача Коши 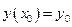 , где
, где  имеет единственное решение.
имеет единственное решение.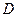 может быть получено единственное решение
может быть получено единственное решение 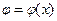 удовлетворяющее условию
удовлетворяющее условию 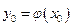 . Перепишем
. Перепишем  ;
; 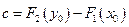 ;
; 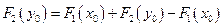 . Рассмотрим
. Рассмотрим  ,
, 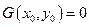 .
.  - непрерывная,
- непрерывная,  - непрерывная. Для
- непрерывная. Для 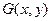 выполняются условия теоремы о неявной функции, значит, найдется
выполняются условия теоремы о неявной функции, значит, найдется 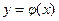 , обращающая уравнение в тождество:
, обращающая уравнение в тождество: 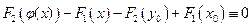 . Дифференцируем по
. Дифференцируем по 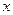 :
: 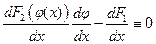 ;
; 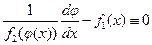 ;
;  . Теорема доказана.
. Теорема доказана.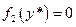 , то
, то  - решение, подозрительное на особое.
- решение, подозрительное на особое.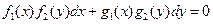
 определены и непрерывны,
определены и непрерывны, 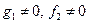 ,
, 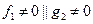 . Тогда общий интеграл дается квадратурой
. Тогда общий интеграл дается квадратурой 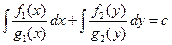 и задача Коши
и задача Коши 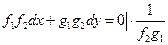 . Если
. Если  , то
, то 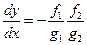 . Сомножители непрерывны, значит, по предыдущей теореме
. Сомножители непрерывны, значит, по предыдущей теореме  , то
, то 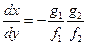 и общий интеграл определяется аналогично. Теорема доказана.
и общий интеграл определяется аналогично. Теорема доказана.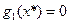 , то
, то  - решение, подозрительное на особое. Если
- решение, подозрительное на особое. Если 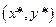 - особая.
- особая.
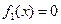 .
.
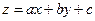 , где
, где 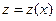 - новая неизвестная функция приводит к уравнению с разделяющимися переменными.
- новая неизвестная функция приводит к уравнению с разделяющимися переменными. .
. или
или 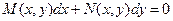 .
.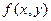 - однородная функция нулевой степени однородности. Уравнение
- однородная функция нулевой степени однородности. Уравнение 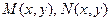 однородные одной степени однородности.
однородные одной степени однородности.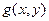 - однородная степени
- однородная степени 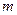 , если
, если 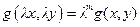 .
.
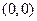 - особая
- особая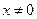 заменой
заменой  , где
, где  - новая неизвестная функция, приводится к уравнению с разделяющимися переменными.
- новая неизвестная функция, приводится к уравнению с разделяющимися переменными.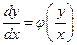 :
: 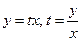 ;
; 
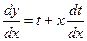 ;
; 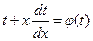 , значит
, значит  . Подозрительными на особые являются решения
. Подозрительными на особые являются решения 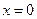 и
и 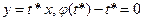 .
. .
.


