
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ДУ-1-ПРОП. Решение. Общее решение, частное решение. Общий интеграл. Задача Коши. Существование и единственность решения задачи Коши.Содержание книги
Поиск на нашем сайте
Основные понятия о ДУ. ДУ – уравнения, в которые входят не только неизвестные функции, но и их производные. Если искомая функция зависит от одной независимой переменной, то такое ДУ – обыкновенное. Если же она зависит от нескольких переменных, то это уравнение в частных производных. Может рассматриваться как одно ДУ, так и их система. Обыкновенное ДУ – соотношение Порядок ДУ – порядок старшей производной. Решение ДУ используются при построении математических моделей динамических систем. Динамическая система – система, эволюционирующая с течением времени и допускающая описание в виде состояния. Состояние – описание, по значению которого в данный момент времени можно однозначно указать, значение в любой момент времени. Предполагается, что между состояниями динамической системы и точками фазового пространства установлено взаимнооднозначное и взаимнонепрерывное соответствие. Математическая модель динамического процесса – совокупность фазового пространства Этапы построения матмодели: 1) Выбор и идеализация 2) Выбор переменных, характеризующих состояние и введение систем их отсчета. 3) Выбор физического закона и построение оператора 4) Построение приведенной модели. Качественное исследование ДУ-1-ПРОП. Изоклины. Линия экстремумов и линия перегибов интегральных кривых. Качественное исследование – построение ИК, исходя из свойств Этапы качественного решения: 1) найти область определения с учетом 2) найти кривые, подозрительные на особое решение (нарушена непрерывность 3) найти главные изоклины (геометрическое место точек, в которых наклон поля одинаков). 4) выделить область монотонности ИК. 5) установить симметрию ИК относительно осей координат. Если уравнение не меняется при замене
6) Найти линию экстремумов ИК – геометрическое место точек 7) Найти линию перегиба ИК, т.е. геометрическое место точек Однородные ДУ 1 порядка
Уравнение Функция Свойства однородного уравнения: 1) Для 2) Точка 3) Изоклины – прямые, проходящие через 4) ИК симметричны относительно Теорема: однородное уравнение для Доказательство:
Иногда удобнее делать замену ДУ Лагранжа
Предположим, что Пусть найдено общее решение Если есть такие ДУ Клеро
Предположим, что Решим введением параметра
Если Если
Существует сокращенный способ решения ДУ Клеро. Общее решение получается заменой
Основные понятия о ДУ. ДУ – уравнения, в которые входят не только неизвестные функции, но и их производные. Если искомая функция зависит от одной независимой переменной, то такое ДУ – обыкновенное. Если же она зависит от нескольких переменных, то это уравнение в частных производных. Может рассматриваться как одно ДУ, так и их система. Обыкновенное ДУ – соотношение Порядок ДУ – порядок старшей производной. Решение ДУ используются при построении математических моделей динамических систем. Динамическая система – система, эволюционирующая с течением времени и допускающая описание в виде состояния. Состояние – описание, по значению которого в данный момент времени можно однозначно указать, значение в любой момент времени. Предполагается, что между состояниями динамической системы и точками фазового пространства установлено взаимнооднозначное и взаимнонепрерывное соответствие. Математическая модель динамического процесса – совокупность фазового пространства Этапы построения матмодели: 1) Выбор и идеализация 2) Выбор переменных, характеризующих состояние и введение систем их отсчета. 3) Выбор физического закона и построение оператора 4) Построение приведенной модели. ДУ-1-ПРОП. Решение. Общее решение, частное решение. Общий интеграл. Задача Коши. Существование и единственность решения задачи Коши.
Задача Коши: Рассмотрим уравнение Общий интеграл: Общее решение может быть записано в форме Коши. Роль произвольной постоянной играет
Теорема Коши-Пикара: пусть дано уравнение Достаточное условие выполнение условия Липшица – существование Доказательство: по т. Лагранжа
Теорема Пеано: пусть дано уравнение
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.104.16 (0.011 с.) |

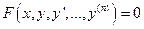 , связывающее независимую переменную
, связывающее независимую переменную 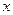 , искомую функцию
, искомую функцию  и ее производную.
и ее производную.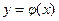 , непрерывная,
, непрерывная, 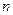 раз дифференцируемая и обращающая уравнение в тождество.
раз дифференцируемая и обращающая уравнение в тождество. , где
, где  - однозначный оператор. Переменные, описывающие состояние – фазовые. Пространство фазовых переменных – фазовое.
- однозначный оператор. Переменные, описывающие состояние – фазовые. Пространство фазовых переменных – фазовое.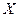 , интервала изменения времени
, интервала изменения времени  и оператора
и оператора 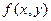 , минуя нахождение общего решения.
, минуя нахождение общего решения.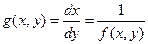
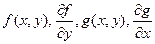 )
)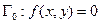 ,
, 
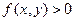 : ИК
: ИК 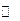 ;
;  : ИК
: ИК 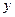 на
на 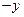 и
и  на
на 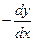 , то есть симметрия относительно
, то есть симметрия относительно 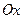 . Если уравнение не меняется при замене
. Если уравнение не меняется при замене 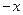 и
и  на
на 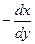 , то есть симметрия относительно
, то есть симметрия относительно 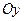 .
.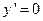 , т.е. изоклина горизонтального наклона, если
, т.е. изоклина горизонтального наклона, если 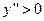 , то экстремум будет минимумом,
, то экстремум будет минимумом, 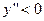 - максимумом. Эти неравенства эквивалентны
- максимумом. Эти неравенства эквивалентны 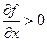 и
и 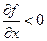 соответственно.
соответственно.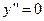 (
(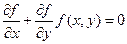 )
) или
или 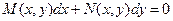 .
.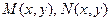 однородные одной степени однородности.
однородные одной степени однородности.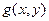 - однородная степени
- однородная степени 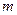 , если
, если 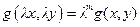 .
.
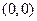 - особая
- особая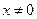 заменой
заменой  , где
, где  - новая неизвестная функция, приводится к уравнению с разделяющимися переменными.
- новая неизвестная функция, приводится к уравнению с разделяющимися переменными.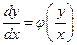 :
: 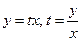 ;
; 
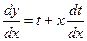 ;
; 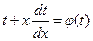 , значит
, значит  . Подозрительными на особые являются решения
. Подозрительными на особые являются решения 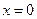 и
и 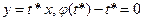 .
. .
.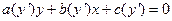 - ДУ Лагранжа.
- ДУ Лагранжа.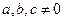 одновременно,
одновременно, 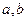 - непрерывные. Пусть
- непрерывные. Пусть 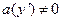 , тогда разрешим уравнение относительно
, тогда разрешим уравнение относительно  . Пусть
. Пусть 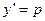 , тогда
, тогда 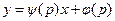 ,
, 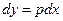 ,
, 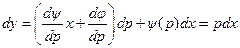 ,
,  . Если
. Если 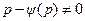 , то можно разрешить по
, то можно разрешить по 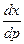 :
: 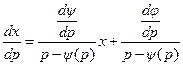 . Получено линейное уравнение первого порядка, оно всегда интегрируемо в квадратурах, поэтому ДУ Лагранжа также всегда интегрируемо в квадратурах.
. Получено линейное уравнение первого порядка, оно всегда интегрируемо в квадратурах, поэтому ДУ Лагранжа также всегда интегрируемо в квадратурах.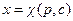 , тогда общее решение ДУ Лагранжа имеет вид
, тогда общее решение ДУ Лагранжа имеет вид 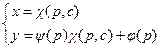 .
.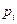 , что
, что  , тогда
, тогда  будут решениями.
будут решениями.  - это так называемые интегральные прямые уравнения Лагранжа. Среди них могут быть особые решения.
- это так называемые интегральные прямые уравнения Лагранжа. Среди них могут быть особые решения.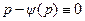 , т.е.
, т.е. 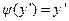 и ДУ имеет вид
и ДУ имеет вид 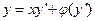 , то это ДУ Клеро.
, то это ДУ Клеро. ,
, 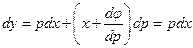
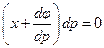
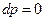 , то
, то  , и
, и 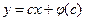 - общее решение ДУ Клеро (прямые).
- общее решение ДУ Клеро (прямые).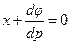 ,
, 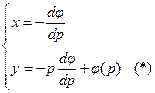 ,
,  ,
,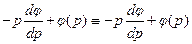 , значит, это решение. Если заменить
, значит, это решение. Если заменить  на с, то получим общее решение уравнения Клеро. Найдем кривые, подозрительные на особое решение с помощью огибающей:
на с, то получим общее решение уравнения Клеро. Найдем кривые, подозрительные на особое решение с помощью огибающей: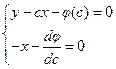 ,
, 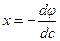 ,
,  - решение (*). Возьмем
- решение (*). Возьмем  и параметр
и параметр 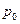 :
: 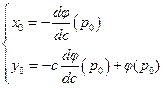 ,
, 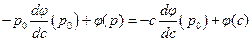 , значит,
, значит, 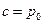 .
. 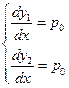 , значит, (*) – особое решение.
, значит, (*) – особое решение. . Особое решение – огибающая этого семейства прямых. Если
. Особое решение – огибающая этого семейства прямых. Если 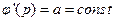 , т.е.
, т.е.  , то вместо особого решения имеем особую точку
, то вместо особого решения имеем особую точку 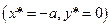 , через которую проходят все интегральные прямые
, через которую проходят все интегральные прямые 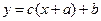 .
. - уравнение разрешенное относительно производной. Решение – непрерывная и дифференцируемая функция
- уравнение разрешенное относительно производной. Решение – непрерывная и дифференцируемая функция 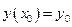 .
.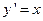 .
.  - общее решение. Пусть поставлена задача Коши
- общее решение. Пусть поставлена задача Коши 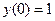 , тогда
, тогда 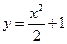 - частное решение.
- частное решение. .
.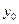 при некотором значении
при некотором значении 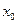 , т.е. надо решить задачу Коши
, т.е. надо решить задачу Коши  ;
;  ;
; 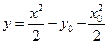 - общее решение в форме Коши.
- общее решение в форме Коши. выполняются условия: 1)
выполняются условия: 1) 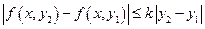 , где
, где 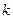 - константа Липшица. Тогда задача Коши имеет одно решение, определенное, непрерывное и непрерывно дифференцируемое, по крайней мере, в окрестности
- константа Липшица. Тогда задача Коши имеет одно решение, определенное, непрерывное и непрерывно дифференцируемое, по крайней мере, в окрестности 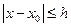 , где
, где  .
.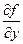 .
.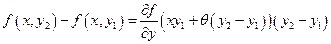 .
.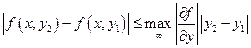 .
.


