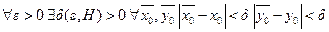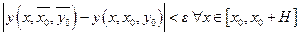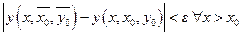Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о продолжении решения задачи Коши. Продолжаемые и непродолжаемые решения.Содержание книги
Поиск на нашем сайте
В теореме Коши-Пикара доказано существование и единственность решения задачи Коши на Решение Решение, продолжаемое вправо и/или влево – продолжаемое. Решение, не продолжаемое ни вправо, ни влево – непродолжаемое. Теорема: при выполнении теоремы Коши-Пикара в ограниченной замкнутой области Теорема: если Таким образом, ИК может быть непродолжаемой ввиду приближения к точке нарушения условий Коши-Пикара или ввиду приближения к асимптоте. Теорема о непрерывной зависимости решения задачи Коши от параметров. Теорема: пусть функция Доказательство: аналогично доказательству теоремы Коши-Пикара. 1) 2) Рассмотрим последовательность пикаровых приближений: Все оценки сохраняются, т.к. Теорема о непрерывной зависимости решения задачи Коши от начальных условий. Теорема: пусть дано Доказательство: сведем вопрос о зависимости от начальных условий к вопросу зависимости от параметров:
Если
Решение, для которого близость сохраняется при любых больших значениях аргумента – устойчивое, т.е.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 976; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.148.57 (0.01 с.) |

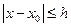 . Если
. Если 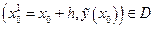 , то вокруг этой точки можно построить прямоугольник, в котором будут выполняться условия теоремы Коши-Пикара. Необходимо получить единственное решение
, то вокруг этой точки можно построить прямоугольник, в котором будут выполняться условия теоремы Коши-Пикара. Необходимо получить единственное решение  на
на  , причем
, причем 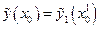 , следовательно, по теореме Коши-Пикара они будут совпадать на отрезке.
, следовательно, по теореме Коши-Пикара они будут совпадать на отрезке.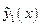 - продолжение решения
- продолжение решения 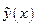 . Аналогичные рассуждения проводятся, пока не получаем точку на границе
. Аналогичные рассуждения проводятся, пока не получаем точку на границе 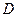 .
. решение
решение 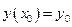 продолжаемо до границы.
продолжаемо до границы.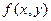 определена и непрерывна в
определена и непрерывна в 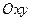 и удовлетворяет условию Липшица во всякой ограниченной области этой плоскости, то всякая ИК неограниченно продолжаема до
и удовлетворяет условию Липшица во всякой ограниченной области этой плоскости, то всякая ИК неограниченно продолжаема до 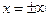 или имеет вертикальную асимптоту при конечном
или имеет вертикальную асимптоту при конечном 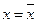 .
. в области
в области 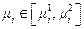 удовлетворяет условиям: 1) определена и непрерывна по совокупности
удовлетворяет условиям: 1) определена и непрерывна по совокупности 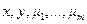 ; 2)
; 2) 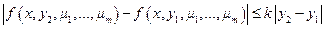 ; 3)
; 3) 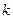 не зависит от
не зависит от 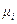 . Тогда можно указать промежуток
. Тогда можно указать промежуток  определено единственное решение
определено единственное решение  и
и 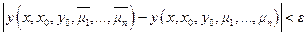 .
.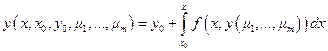
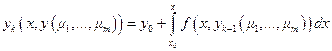
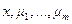 , равномерно сходится к точному решению, непрерывному по
, равномерно сходится к точному решению, непрерывному по  - уравнение (1).
- уравнение (1). 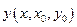 , непрерывно зависящее от начального условия, т.е.
, непрерывно зависящее от начального условия, т.е. 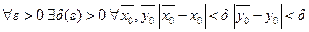

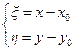 , т.е.
, т.е.  ,
, 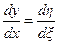 ,
, 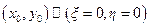 ,
,  .
.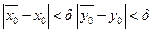 , то по теореме о непрерывной зависимости решения задачи Коши от параметров, задача Коши имеет единственное решение, непрерывно зависящее от
, то по теореме о непрерывной зависимости решения задачи Коши от параметров, задача Коши имеет единственное решение, непрерывно зависящее от 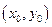 -
- 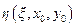 .
.  .
.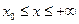 , т.е.
, т.е.  .
.