
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок решения: с использованием функции Поиск решения.Содержание книги
Поиск на нашем сайте 1.Введем в ячейку В17 формулу 3*С11^2+2*C11-15. В ячейку С17 введем начальное значение х=-1. Результат приведен на рис. 2 в столбцах В и С.
2.Введем команду Сервис, Поиск решения – открывается одноименное окно диалога (рис. 4.).
Второй корень можно найти при любом начальном значении Х, если установить ограничения на его значение. Щелкните по кнопке Добавить в окне диалога Поиск решения (рис. 4). Открывается окно диалога “Добавление ограничения” (рис. 6). Выберите в списке “Ссылка на ячейку” адрес ячейки, содержащей значение х, например, D20, в среднем списке - знак отношения, а в списке “Ограничения” введите значение ограничения, например, “0” и щелкните по кнопке ОК. Результат будет записан в окне “Ограничения” окна диалога Поиск решения (рис. 4). Пример решения приведен в строке 20 (рис. 2). Из анализа результатов на рис. 2 можно сделать следующие выводы: Функция Поиск решения дает более точные результаты по сравнению с функцией Подбор параметра, при этом результат не зависит от начального приближения. Функция может найти только одно решение, поэтому поиск значения корня необходимо вести на отрезке отделения. Пример 3. Задача о “пожарном ведре”. Дана заготовка из жести в виде круга диаметром R=0,75 м. Требуется выкроить из него конусообразное ведро таким образом, чтобы объем ведра был наибольший (рис. 7). Разработаем математическую модель: Объем пожарного ведра Q=1/3hSосн, Sосн= pr2, где r – радиус основания конуса, h – высота ведра, h=корень(R2-r2)
r=(2p-a)R/ (2p),
Библиографический список
1. Информатика. Базовый курс. 2-е издание / Под ред. С. В. Симоновича. — СПб.: Питер, 2005. — 640 с: ил. 2. Анеликова Л. А. Лабораторные работы по Excel. - M.: СОЛОН-ПРЕСС. 2006 128 с: ил. — (Серия «Элективный курс • Профильное обучение») 3. Excel. Единый справочник/В. Н. Шитов. — М.: ГроссМедиа, 2005. - 512 с. 4. Решение математических задач средствами Excel: Практикум /В. Я. Гельман. — СПб.: Питер, 2003. — 240 с: ил. 5. Быков В. Л., Ашаев Ю. П. Основы информатики. Пособие. – Брест, Издательство БрГТУ, 2006
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

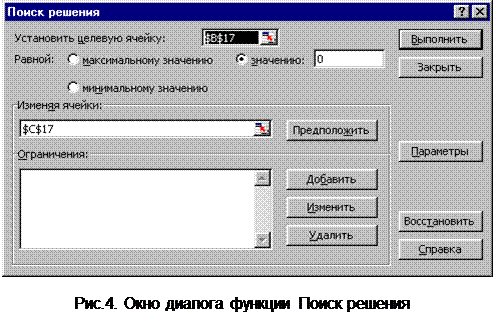
 Введем в строку “Установить целевую ячейку” адрес ячейки, содержащей формулу В17, установим переключатель Значение и в строку вода “значению” введем значение “0”, а в строку “Изменяя ячейки” введем адрес ячейки содержащий значение Х - С17 с абсолютным адресом. Щелкнем по кнопке Выполнить. Открывается окно “Результаты поиска решения” (рис. 5). Для получения результата щелкните по кнопке ОК. В ячейке В17 отобразится значение точности поиска решения, а в ячейке С17- значение корня. Для сравнимости результатов на рис. 2 результаты помещены в столбцах E и F. Результат решения не зависит от выбранного начального значения корня. Сравните результаты в строках 17 и 18. Однако Функция Поиск решения, также как и функция Подбор параметра позволяет найти только один корень уравнения. Для получения значения второго корня необходимо изменить начальное значение. В строке 19 приведен результат поиска второго корня.
Введем в строку “Установить целевую ячейку” адрес ячейки, содержащей формулу В17, установим переключатель Значение и в строку вода “значению” введем значение “0”, а в строку “Изменяя ячейки” введем адрес ячейки содержащий значение Х - С17 с абсолютным адресом. Щелкнем по кнопке Выполнить. Открывается окно “Результаты поиска решения” (рис. 5). Для получения результата щелкните по кнопке ОК. В ячейке В17 отобразится значение точности поиска решения, а в ячейке С17- значение корня. Для сравнимости результатов на рис. 2 результаты помещены в столбцах E и F. Результат решения не зависит от выбранного начального значения корня. Сравните результаты в строках 17 и 18. Однако Функция Поиск решения, также как и функция Подбор параметра позволяет найти только один корень уравнения. Для получения значения второго корня необходимо изменить начальное значение. В строке 19 приведен результат поиска второго корня. Радиус основания зависит от угла вырезки a. Длина окружности основания ведра l=(2p-a)R или l=2pr, отсюда
Радиус основания зависит от угла вырезки a. Длина окружности основания ведра l=(2p-a)R или l=2pr, отсюда



