
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование Excel для вычисленийСодержание книги
Поиск на нашем сайте Решение систем линейных алгебраических уравнений Для решения систем линейных алгебраических уравнений (СЛАУ) применяют аналитические и численные методы. Электронная таблица Excel не имеет функций для решения систем уравнений, формулы для вычисления матриц необходимо формировать самостоятельно, используя известные методы, например метод Крамера или метод Гаусса (метод исключения переменных). Однако, используя встроенные функции МОБР, МУМНОЖ и МОПРЕД эти операции выполняются достаточно легко. Например, можно воспользоваться формулой вычисления вектора неизвестных через обратную матрицу и вектор свободнх членов: Операции с матрицами Электронная таблица позволяет выполнять линейные преобразования матриц: умножение, деление матриц на число, прибавление или вычитание чисел, а также операции над матрицами: сложение, умножение матриц, транспонирование, вычисление определителей. Средствами Excel можно решать и системы линейных алгебраических уравнений. Для этой цели электронная таблица имеет ряд функций для работы с матрицами: МОПРЕД(массив) – вычисление определителя матрицы; МОБР(массив) – вычисление обратной матрицы; МУМНОЖ(массив; массив) – умножение матриц; ТРАНСП(массив) – транспонирование матриц. Примеры операций с матрицами приведены на Рис. 5.1. Обратите внимание на разные результаты, получаемые при умножении матриц с использованием оператора умножения “*”, и с использованием функции МУМНОЖ. В первом случае каждый элемент матрицы результата равен произведению соответствующих элементов сомножителей, во втором случае каждый элемент матрицы вычисляется по формуле
Рис. 5.1. Операции с матрацами в Excel
Алгоритм выполнения операций над матрицами сводится к следующим операциям: - выделить ячейку или область, если результатом выполнения операции будет матрица, куда будет помещаться результат вычисления; - ввести в строку ввода символ “=”; - ввести в строку ввода первый операнд; - ввести в строку ввода символ операции; - ввести в строку ввода второй операнд; - нажать комбинацию клавиш Ctrl+Shift+Enter для вставки формулы в выделенную область. Контрольные вопросы 1. Что такое расширенная матрица коэффициентов системы линейных уравнений? 2. Что является решением системы линейных алгебраических уравнений? 3. Какие методы применяются для решения СЛАУ в электронной таблице? 4. Напишите алгоритм решения СЛАУ методом Крамера. 5. Напишите алгоритм решения СЛАУ матричным методом с использованием обратной матрицы. 6. Назовите функции электронной таблицы для работы с матрицами. 7. Какие методы используются для решения нелинейных систем уравнений? Лабораторная работа №5
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 .
.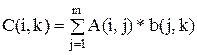 , где m – число столбцов в матрице A, k – число столбцов в матрице.
, где m – число столбцов в матрице A, k – число столбцов в матрице.


