Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка на нормальность остатковСодержание книги
Поиск на нашем сайте
Для понимания адекватности построенной модели многомерной линейной регрессии исследуются регрессионные остатки. Если выбранная модель регрессии хорошо описывает истинную зависимость, то остатки должны быть независимыми нормально распределенными случайными величинами с нулевым средним, и в их значениях должен отсутствовать тренд. Анализ регрессионных остатков – это и есть процесс проверки выполнения этих условий. В эконометрике очень полезно, если ошибки имеют нормальное распределение. В таком случае исследователь сразу может получить надёжные оценки для ошибок коэффициентов и интервалы для коэффициентов. Добавим в нашу модель бинарную переменную HOT, принимающую значение 1 в случае, если путевка «горящая» и 0, если нет, и исследуем модель на нормальность остатков. Снова введем тестируемую и альтернативную гипотезы:
Выполняем следующие действия: View→ Residual Diagnostics→Histogram-Normality Test
Визуальный анализ Диаграмма рассеяния Построим диаграмму рассеяния зависимости переменной PRICE от TIME, т.е. посмотрим, как влияет продолжительность отдыха на цену турпутевки. Для этого выделим правой кнопкой мыши зависимую переменную PRICE, затем удерживая клавишу ctrl выделим объясняющую переменную TIME. Кликом правой кнопки мыши выбираем опцию Open, далее выбираем Open Group (открыть в одной группе).
Пакет открывает группу с именем UNTITLED, в которую входят выделенные переменные (серии).
Открываем на рабочей поверхности вкладку View→Graph
В поле Тип графа выбираем Basic graph и Specific: Scatter →OK
Получаем следующий результат:
По диаграмме можно заметить следующую зависимость: с увеличением значения переменной TIME, увеличивается и значение PRICE, т.е. чем больше дней отдыха предусматривает путевка, тем выше ее цена, что логично. Построение Box Plot Перейдем к построению ящичковой диаграммы, или по-другому, диаграммы Ящик с усами (англ. Box and Whisker Chart, Box Plot). Такая диаграмма обычно используется для отображения статистического анализа. Простая ящичковая диаграмма отображает диапазон данных, находящийся между первым и третьим квартилем (25-й и 75-й процентили соответственно), а медиана- линия в середине ящика делит его на две части (50-й процентиль) (межквартильный диапазон). Усы отображают данные первого квартиля — от второго квартиля до минимального значения, и четвертого квартиля – от третьего до максимального значения. Концы усов — края статистически значимой выборки (без выбросов). Данные, выходящие за границы усов (выбросы), отображаются на графике в виде жирных точек.
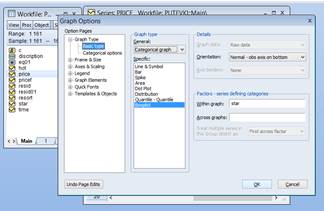
Построим Box Plot для нашего примера. Определим базовое значение числа звезд отеля по переменной STAR. Для этого выделяем зависимую переменную, правой кнопкой мыши выбираем Open, открывается окно со значениями данной переменной.
View→ Graph
Далее выбираем тип графа. В поле General выбираем Categorical graph, в Specific: Boxplot. В поле Within graph вписываем название объясняющей переменной, по которой будет построен граф.
Получаем следующую диаграмму:
Теперь, исходя из полученных данных, выберем базу. Критерии отбора такие: значения выбросов («жирные точки») должны быть отдалены на минимальное расстояние от медианы, и выбираем ящик с самыми короткими усами, которые обозначают края статистически значимой выборки (без выбросов). Проведя визуальный анализ на основе выше описанных критериев, определяем как базу переменную STAR=3 Теперь расширим нашу модель, добавив в нее группу переменных STAR=3, STAR=4, STAR=5, разделив STAR на 3 переменных и выбрав базу STAR=3 командой @expand(star, @drop(3))
Получим:
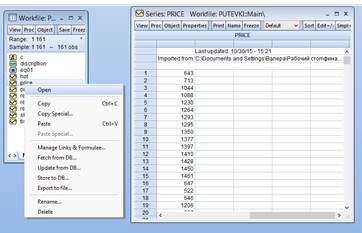
Прокомментируем полученные рассчеты. Опять заметим, что Prob(F-statistic)<0,01, следовательно уравнение значимо. Значимость STAR оценивается таким образом: если хотя бы одна переменная из STAR=4, STAR=5 значима т.е. Нормальность остатков Также можно осуществить визуальный анализ остатков. Выделяем RESID (переменную, в которую записываются остатки)→Open→View→Graph→General: Basic graph→Specific: Quantile-Quantile →OK
Видно, что остатки не сильно, но все-таки отстают от линии тренда.
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.145 (0.005 с.) |





 , следовательно, принимаем гипотезу о том, что остатки не имеют нормального распределения.
, следовательно, принимаем гипотезу о том, что остатки не имеют нормального распределения.









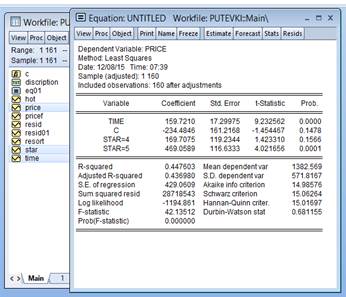
 =0,0001 следовательно уже можно утверждать о значимости всей группы переменных STAR. Видим, что по сравнению с предыдущей моделью,
=0,0001 следовательно уже можно утверждать о значимости всей группы переменных STAR. Видим, что по сравнению с предыдущей моделью,  увеличился, следовательно, мы можем утверждать что данное уравнение лучше представляет выборку.
увеличился, следовательно, мы можем утверждать что данное уравнение лучше представляет выборку.