Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка на гетероскедастичностьСодержание книги
Поиск на нашем сайте
Эконометрический метод складывался в преодолении показателей, которые искажают результаты применения классических статистических методов: · эффекта гетероскедастичности, т.е. отсутствия нормального распределения остатков для регрессионной функции; · ассиметричности связей; · мультиколлинеарности объясняющих переменных; · закрытости механизма связи между переменными в изолированной регрессии; · автокорреляции; · должной корреляции; · наличия лагов. Разберемся подробнее с первым термином. Гетероскедастичность (англ. heterosсedasticity) — понятие, означающее неоднородность наблюдений, которая выражается в неодинаковой (непостоянной) дисперсии случайных ошибок регрессионной модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели, в этом состоит 4 предпосылка КЛММР. Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с результате применения метода наименьших квадратов. Кроме этого, оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Таким образом, статистические выводы о качестве полученных оценок могут быть неадекватными. Ввиду этого тестирование моделей на наличие гетероскедастичности представляет собой одну из необходимых процедур при построении эконометрических моделей. Наличие гетероскедастичности можно заметить на графиках остатков регрессии (или их квадратов) по некоторым переменным, по оцененной зависимой переменной или по номеру наблюдения. На этих графиках разброс точек может меняться в зависимости от значения этих переменных. Для более строгой проверки применяют такие статистические тесты как тест Уайта, Голдфелда — Куандта, Бройша — Пагана, Парка, Глейзера, Спирмена. Проверим нашу модель зависимости цены туристической путевки от продолжительности отдыха и уровня комфортабельности отеля на гетероскедастичность. Сформулируем две гипотезы:
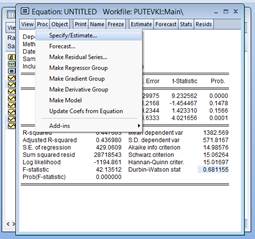
Во вкладке View выбираем Residual Diagnostics, затем Heteroskedasticity Tests
Из предложенного списка выбираем тест Уайта.
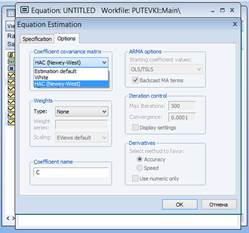
Все значения Тест Уайта является наиболее общим тестом и имеет некоторые недостатки: · даже при небольшом количестве регрессоров в исходной модели во вспомогательной модели, которая оценивается на втором шаге, оцениваемых коэффициентов может быть «много» (относительно объема выборки), что уменьшает мощность теста; · если нулевая гипотеза отвергается, то нет указаний на функциональную форму гетероскедастичности (на вид функции · тест не учитывает зависимость дисперсии случайных ошибок от невключенных в модель регрессоров. Что же делать в условиях гетероскедастичности? Как было сказано выше: оценки коэффициентов не смещены (хоть и неэффективны). Смещены и несостоятельны стандартные ошибки. Один из подходов к решению проблемы — вычисление состоятельных (робастных к гетероскедастичности) стандартных ошибок. При наличии гетероскедастичности, но без автокорреляции, вместо диагональных элементов ковариационной матрицы случайных ошибок можно использовать квадраты остатков и получить состоятельные оценки (стандартные ошибки в форме Уайта). В общем случае, кроме гетероскедастичности, может иметь место также и автокорреляция некоторого порядка. Следовательно, кроме диагональных элементов, необходимо оценить внедиагональные элементы, отстоящие от диагонали, что и сделали Ньюи и Уест (Newey, West).
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.111 (0.005 с.) |

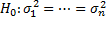
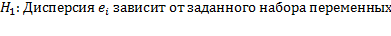


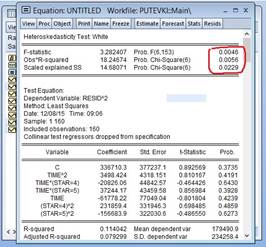
 , следовательно принимаем гипотезу
, следовательно принимаем гипотезу 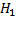 о наличии гетероскедастичности в нашей модели.
о наличии гетероскедастичности в нашей модели.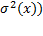
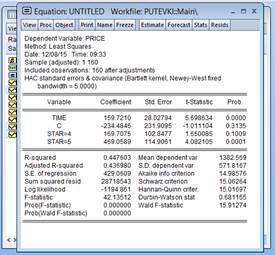
 Возвращаемся к таблице расчётов по нашей модели: View→ Estimation Output. Смотрим на значение критерия Дарбина-Уотсона статистический критерий, применяемого для тестирования автокорреляции первого порядка. Если
Возвращаемся к таблице расчётов по нашей модели: View→ Estimation Output. Смотрим на значение критерия Дарбина-Уотсона статистический критерий, применяемого для тестирования автокорреляции первого порядка. Если 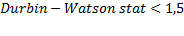 , делаем подправку в форме Ньюи-Уеста.
, делаем подправку в форме Ньюи-Уеста.