
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рассмотрим критерии Манна-Уитни и Вилкоксона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Критерий Манна-Уитни и критерий Вилкоксона – критерии ранговые, т.е. основанные на сравнении сумм рангов, полученных тем или иным образом из сравниваемых выборочных распределений. В данном конкретном случае рангом называется порядковыйномер числа в ранжированном (расставленном в порядке возрастания) массиве данных – чем больше число, тем выше его ранг. При этом, если числа не повторяются, то их ранги в точности соответствуют их порядковым номерам. Если же некое число повторяется несколько раз, то всем им приписывается средний ранг. Продемонстрируем, как все это происходит и выглядит. Допустим, мы получили следующий вариационный ряд данных x: 5.6 11.7 -3.5 6.3 8 7.4 0.5 8 3 3.1 15.2 3.1 8 6.7 111 4.4 Здесь числа представлены в том порядке, как они были получены. Расставим их в порядке возрастания и припишем порядковые номера, а также ранги R:
Из приведенного примера хорошо видно, что при ранжировании происходит «линеаризация данных» - сглаживание их резких колебаний за счет того, что ранг числа не зависит от его абсолютной величины и разницы с соседними вариантами. Например, последнее число 111 чуть ли не на порядок превышает ближайшее к нему 15.2. Тем не менее, ранг его всего на 1 выше, чем у предпоследнего числа. Ранговые критерии для сравнения выборочных совокупностей делятся на две группы – для независимых и зависимых выборок. Критерий Манна-Уитни – ранговый критерий для сравнения независимых выборок. Критерий парных сравнений Вилкоксона– ранговый критерий для сравнения зависимых выборок. Рассмотрим его на примере. У 10 здоровых взрослых людей измеряли кровяное давление после введения кофеина и плацебо. Получены следующие данные для «верхнего», систолического давления СД:
Возникает вопрос, можно ли на основании этих данных полагать, что кофеин оказывает физиологическое действие. Вначале значения одного ряда строго попарно вычитают из значений другого с учетом знака разницы d. Вычтем нижний ряд из верхнего:
Далее разницы ранжируют по известным правилам, но при этом не учитывают знак разницы (т.е. ранжируют по модулю). Нулевую пару отбрасывают.
Отдельно суммируют ранги для положительных и отрицательных разниц. В нашем случае получаем: Смысл теста состоит в следующем. Если бы мы имели бесконечно большой ряд случайных разниц, то число и величина положительных разниц равнялись бы числу отрицательных и, соответственно, суммы их рангов были бы равны. На конечном и ограниченном числовом массиве опять же чисто случайно может иметь место «перекос» в сторону преимущественно положительных или отрицательных разниц. Это обстоятельство и учитывается в критических значениях критерия. Tкр – это граница между практически возможными и практически невозможными значениями критерия. Соответственно, если Как было показано выше, пары, имеющие одинаковые числовые значения и, соответственно, дающие нулевые разницы, исключаются из рассмотрения. И если таких случаев много, то «жесткость» критерия нарастает, поскольку Tкр тем меньше, чем меньше сравниваемых пар. Соответственно, увеличивается число ситуаций, когда нулевую гипотезу отвергнуть невозможно, и различие будет считаться незначимым. Более того, если число пар окажется меньше 6, то критерий Вилкоксона вообще перестанет «работать»: 6 - минимальное число пар, для которого еще существует Tкр. Для меньшего числа его просто невозможно рассчитать. А подобные ситуации в медико-биологической практике возникают довольно часто, поскольку многие измерения неизбежно приходится выполнять с достаточно высокой степенью грубости, и вероятность появления совпадающих значений здесь все еще весьма высока.
13. Функциональная и корреляционная зависимость. Прямая, обратная связь. Любые явления в окружающем нас мире могут быть связаны прямой или обратной связью. Эта характеристика называется направленностью связи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.55.43 (0.01 с.) |

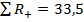 ,
, 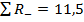 . В качестве значения критерия Tz берут меньшую сумму независимо от знака, т.е. Tz =11,5. Сравниваем это значение с «критическим» из специальной таблицы, входом в которую является число сравниваемых пар, но лишь тех, которые не дают нулевые разницы. В нашем случае таковых 9. Тогда Tкр = 6 для
. В качестве значения критерия Tz берут меньшую сумму независимо от знака, т.е. Tz =11,5. Сравниваем это значение с «критическим» из специальной таблицы, входом в которую является число сравниваемых пар, но лишь тех, которые не дают нулевые разницы. В нашем случае таковых 9. Тогда Tкр = 6 для  и Tкр =2 для
и Tкр =2 для  . Поскольку
. Поскольку 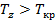 даже для первого уровня значимости, различий уровней СД нулевую гипотезу отвергнуть нельзя и различия не являются статистически значимыми (р<0,05). Иными словами, у нас нет пока оснований утверждать, что действие кофеина носит исключительно физиологический характер.
даже для первого уровня значимости, различий уровней СД нулевую гипотезу отвергнуть нельзя и различия не являются статистически значимыми (р<0,05). Иными словами, у нас нет пока оснований утверждать, что действие кофеина носит исключительно физиологический характер. , то наблюдаемое различие положительных и отрицательных разниц не могло быть получено случайным образом. Это означает, что смещение значений в сопоставляемых числовых рядах объясняется действием какой-то систематически действующей, неслучайной причины, т.е. носит статистически достоверный (устойчивый и прогнозируемый) характер.
, то наблюдаемое различие положительных и отрицательных разниц не могло быть получено случайным образом. Это означает, что смещение значений в сопоставляемых числовых рядах объясняется действием какой-то систематически действующей, неслучайной причины, т.е. носит статистически достоверный (устойчивый и прогнозируемый) характер.


